1. 无向图与开放树
在讲最小生成树之前,先来说一说开放树。连通而无环路的无向图称做开放树。如果指定开放树中某一顶点为根,并且把每一条边看成是背离根的,则一棵开放树变成一棵树。
开放树有2个性质:
- 具有n>=1个顶点的开放树包含n-1条边
- 如果在开放树中任意增加一条边,将构成一个环路
如下列两个图:
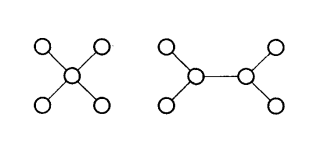
2. 最小生成树
只针对无向图
假设E中的每条边都有权重,为c(u,v),也叫做边长。图G的一棵生成树是连接V中所有顶点的一棵开放树。将生成树中所有边长的总和称为生成树的价。使这个价最小的生成树称为图的最小生成树。
设G=(V,E)是一个连通图,在E上定义一个权函数C,且{(V1,T1),(V2,T2),...,(Vk,Tk)}是G的任意生成森林,令
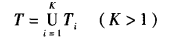
其中,|T| <= |E|,又假设e=(v,w)是E-T中的一条边,其权值C[v][w]最小,而且v在V1中,w不在V1中,则图G有一棵包含T和e的生成树,其价不大于包含T的任何生成树的价。
以上的性质下,两种算法应运而生:Prim算法和Kruskal算法
- Prim算法
/*输入为加权无向图G=(V,E),其中V={1,2,3,...,n}
要点:引进集合U和T,U准备放顶点,T准备放边。初值为U={1},T为空,选择最小权的边(u,v),使u在U中,v在V-U中,将v加入U,(u,v)加入T。重复这个过程 */
void Prim(costtype C[n+1][n+1])
{
/*CLOSECT表示U中的顶点,(i,CLOSECT[i])具有最小的权,而LOWCOST[i]表示该边的权,其中i不在U中 */
costtype LOWCOST[n+1];
int CLOSEST[n+1];
int i,j,k;
costtype min;
for(i=2;i <= n;i++)
{
//初始化
LOWCOST[i] = C[1][i];
CLOSEST[i] = 1;
}
for(i=2;i=n;i++)
{
min = LOWCOST[i];
k=i;
//找出最小权的边
for(j=2;j<=n;j++) {
if(LOWCOST[j] < min) {
min = LOWCOST[j];
k = j;
}
cout<<"("<<k<<","<<CLOSECT[k] << ")"<<endl;
LOWCOST[k] = infinity; /* k加入U */
//对新加入的k的基础上,更新LOWCOST和CLOSECT
for(j = 2;j<=n;j++) {
if(C[k][j] < LOWCOST[j] && LOWCOST[j] != infinity) {
LOWCOST[j] = C[k][j];
CLOSECT[j] = k;
}
}
}
}
- Kruskal算法
void Kruskal(V,T)
{
T = V;
ncomp = n;
while(ncomp > 1) {
从E中取出并删除权最小的边(v,u)
if(v和u属于T中不同的连通分量) {
T= T + (v,u);
ncomp --;
}
}
}
Prim算法复杂度为O(n2),而Kruskal算法复杂度为O(ne),故Prim算法适用于点较少的情况
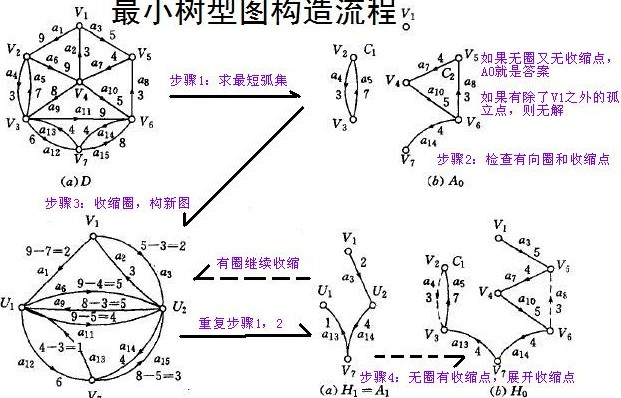
3. 最小树形图
只针对有向图
首先为除根之外的每个点选定一条入边,这条入边一定要是所有入边中最小的。现在所有的最小入边都选择出来了,如果这个入边集不存在有向环的话,我们可以证明这个集合就是该图的最小树形图。这个证明并不是很难。如果存在有向环的话,我们就要将这个有向环缩成一个人工顶点,同时改变图中边的权。假设某点u在该环上,并设这个环中指向u的边权是in[u],那么对于每条从u出发的边(u, i, w),w为权,在新图中连接(new, i, w)的边,其中new为新加的人工顶点; 对于每条进入u的边(i, u, w),在新图中建立边(i, new, w-in[u])的边。
int ZLEdmonds(int n,int map[maxn][maxn])
{
bool visited[maxn],flag[[maxn];
int pre[maxn];
int sum=0,i,j,k;
for( i=0; i<n; i++){
flag[i]=false;
map[i][i]=INF;
}
pre[0]=0;
while( true){
//求最短弧集合E0。
for( i=1; i<n; i++){
if( flag[i]) continue;
pre[i]=i;
for( j=0; j<n; j++){ //pre[i]保存终点为i的最短弧的起点。
if( !flag[j]&&map[j][i]<map[pre[i]][i])
pre[i]=j;
}
if( pre[i]==i) return -1;
}
//检查E0
for( i=1; i<n; i++){
if( flag[i]) continue;
for( j=0; j<n; j++)
visited[j]=false;
visited[0]=true;
j=i;
do{
visited[j]=true;
j=pre[j];
}while( !visited[j]);
if( !j) continue; //没有找到环。
i=j;//将整个环的权值保存,累计入原图的最小树形图
do{
sum+=map[pre[j]][j];
j=pre[j];
}while( j!=i);
j=i;//对于环上的点有关的边,修改边权
do{
for( k=0; k<n; k++){
if( !flag[k]&&map[k][j]&&map[k][j]<INF&&k!=pre[j])
map[k][j]-=map[pre[j]][j];
}
j=pre[j];
}while( j!=i);
//缩点,将整个环缩成i号点,所有环上的点有关的边转移到点i
for( j=0; j<n; j++){
if( j==i) continue;
for( k=pre[i]; k!=i; k++){
if( map[k][j]<map[i][j])
map[i][j]=map[k][j];
if( map[j][k]<map[j][i])
map[j][i]=map[j][k];
}
}
//标记环上其他的点为被缩掉 下次再找Ei时不参与
for( j=pre[i]; j!=i; j=pre[j])
falg[j]=true;
//当前环缩点结束,形成新的图G',跳出继续求G'的最小树形图 ,累计入sum。
}
if( i==n){
for( i=0; i<n; i++)
if( !flag[i])
sum+=map[pre[i]][i];
break;
}
}
return sum;
}