优先级队列
概念
搜索树结构和词典结构,都支持覆盖数据全集的访问和操作。也就是说,其中存储的每一数据对象都可作为查找和访问目标
优先级队列,较之此前的数据结构反而有所削弱。具体地,这类结构将操作对象限定于当前的全局极值者。而维护一个偏序关系
- 接口
template <typename T> struct PQ {
//优先级队列PQ模板类
virtual void insert ( T ) = 0;
//按照比较器确定的优先级次序插入词条
virtual T getMax() = 0;
//叏出优先级最高的词条
virtual T delMax() = 0;
//删除除优先级最高的词条
};
- 应用
/******************************************************************************************
2 * Huffman树极造算法:对传入癿Huffman森枃forest逐步合幵,直刡成为一棵树
3 ******************************************************************************************
4 * forest基亍优先级队列实现,此算法适用亍符合PQ接口癿仸何实现斱式
5 * 为Huffman_PQ_List、Huffman_PQ_ComplHeap和Huffman_PQ_LeftHeap共用
6 * 编译前对应工程叧需讴置相应标志:DSA_PQ_List、DSA_PQ_ComplHeap戒DSA_PQ_LeftHeap
7 ******************************************************************************************/
HuffTree* generateTree ( HuffForest* forest ) {
while ( 1 < forest->size() ) {
HuffTree* s1 = forest->delMax();
HuffTree* s2 = forest->delMax();
HuffTree* s = new HuffTree();
s->insertAsRoot ( Huffchar ( '^', s1->root()->data.weight + s2->root()->data.weight ) );
s->attachAsLC ( s->root(), s1 );
s->attachAsRC ( s->root(), s2 );
forest->insert ( s );
//将合幵后癿Huffman树揑回Huffman森枃
}
HuffTree* tree = forest->delMax();
//至此,森枃中癿最后一棵树
return tree;
//即全尿Huffman编码树
}
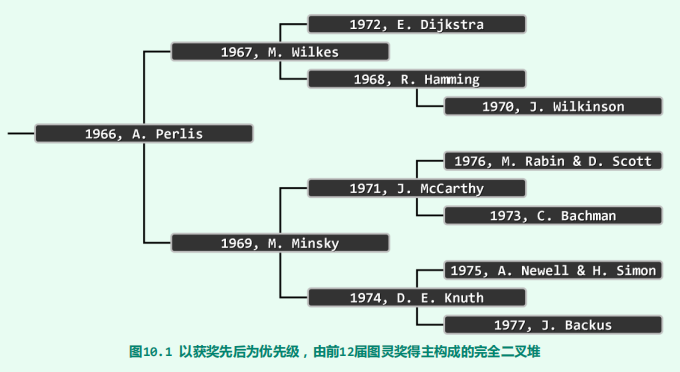
堆
完全二叉堆
- 什么是堆
-
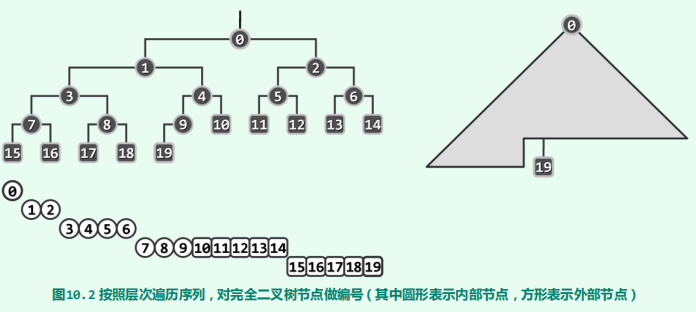
它是一个完全二叉树,即除了最后一层节点不是满的,其他层节点都是满的,即左右节点都有。
-
它不是二叉搜索树,即左节点的值都比父节点值小,右节点的值都不比父节点值小,这样查找的时候,就可以通过二分的方式,效率是(log N)。
-
它是特殊的二叉树,它要求父节点的值不能小于子节点的值。这样保证大的值在上面,小的值在下面。所以堆遍历和查找都是低效的,因为我们只知道从根节点到子叶节点的每条路径都是降序的,但是各个路径之间都是没有联系的,查找一个值时,你不知道应该从左节点查找还是从右节点开始查找。
-
它可以实现快速的插入和删除,效率都在(log N)左右。所以它可以实现优先级队列。
-
大顶堆与小顶堆
堆序性也可对称地约定为“堆顶以外的每个节点都不低(小)于其父节点”,此时同理,优先级最低的词条,必然始终处于堆顶位置。为以示区别,通常称前(后)者为大(小)顶堆 -
模板类与一些常用方法
//必要的方法
int Parent(int i){
//PQ[i]的父节点(floor((i-1)/2),i无论正负)
return ((i - 1) >> 1);
}
int LChild(int i){
//PQ[i]的左孩子
return (1 + (i << 1));
}
int RChild(int i){
//PQ[i]的右孩子
return ((i + 1) << 1);
}
Boolean InHeap(int n,int i){
//判断PQ[i]是否合法
return ((-1 < i) && (i < n));
}
Boolean ParentValid(int i){
return (Parent(i) >= 0);
}
Boolean LChildValid(int n,int i){
//判断PQ[i]是否有一个(左)孩子
return InHeap(n,LChild(i));
}
Boolean RChildValid(int n,int i){
//判断PQ[i]是否有两个孩子
return InHeap(n,RChild(i));
}
int Bigger(Vector<T> PQ,int i,int j){
//取大者(等时前者优先)
return (lt(PQ.elementAt(i),PQ.elementAt(j)) ? j : i);
}
int ProperParent(Vector<T> PQ,int n, int i){
/*父子(至多)三者中的大者*/
return (RChildValid(n,i) ? Bigger(PQ,Bigger(PQ,i,LChild(i)),RChild(i)) :
(LChildValid(n,i) ? Bigger(PQ,i,LChild(i)) : i));
}
//相等时父节点优先,如此可避免不必要的交换
Boolean lt(T a,T b){
return ((int)a > (int)b);
}
void swap(T a,T b){
T c = a;
a = b;
b = c;
}
void copyFrom(T[] A,int lo,int hi){
int i = 0;
while (lo < hi){
this.set(i++, A[lo++]);
}
}
int LastInternal(int n){
return ((n + 1) / 2 - 1);
}
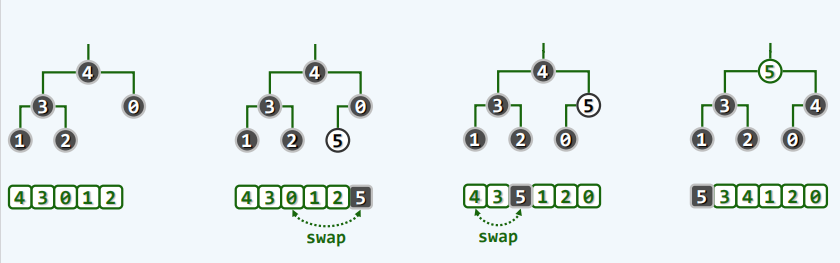
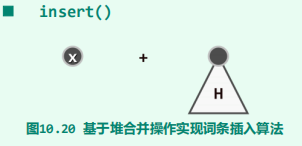
元素插入
-
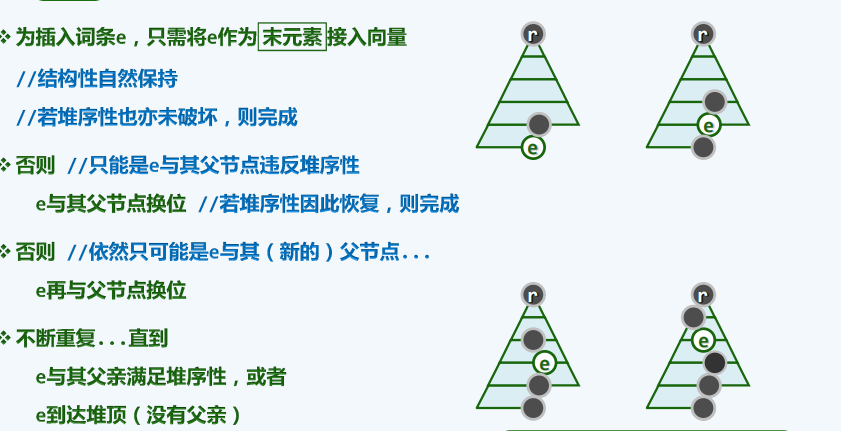
原理
-
实现
@Override
public void insert(T e) {
//插入词条
this.addElement(e);
percolateUp(elementCount - 1);
}
protected int percolateUp(int i){
//上滤
while (ParentValid(i)){
int j = Parent(i);
if (lt(elementAt(i),elementAt(j))) break;
swap(elementAt(i),elementAt(j));
i = j;
}
return i;
}
- 实例
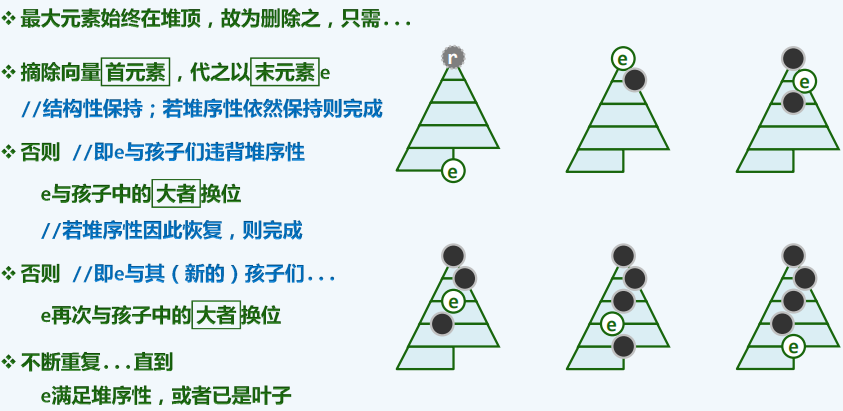
元素删除
-
原理
-
实现
@Override
public T delMax() {
//删除词条
T maxElem = elementAt(0);
this.setElementAt(elementAt(elementCount - 1),0);
this.remove(--elementCount);
percolateDown(elementCount,0);
return maxElem;
}
protected int percolateDown(int n,int i){
//下滤
int j = 0;
while (i != (j = ProperParent(this,n,j))){
swap(elementAt(i),elementAt(j));
i = j;
}
return i;
}
- 实例
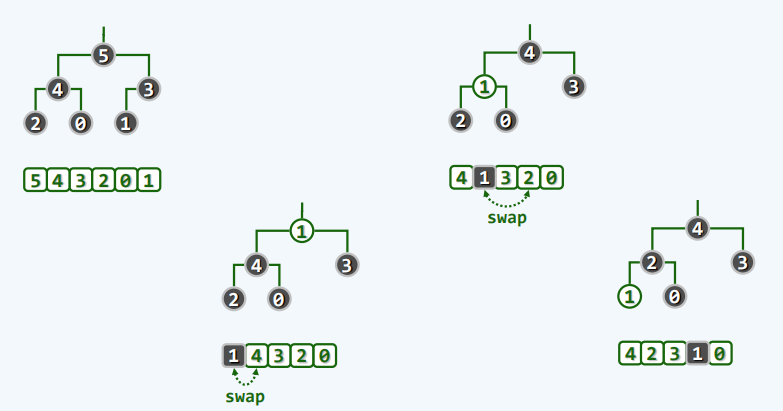
批量建堆
-
原理

-
实现
public PQ_CompHeap(T[] A, int n){
//批量构造
copyFrom(A,0,n);
heapify(n);
}
protected void heapify(int n){
//Floyd建堆算法
for (int i = LastInternal(n);i >= 0;i--){
//自下而上,依次
percolateDown(n,i);
//下滤各内部节点
}
}
protected int percolateDown(int n,int i){
//下滤
int j = 0;
while (i != (j = ProperParent(this,n,j))){
swap(elementAt(i),elementAt(j));
i = j;
}
return i;
}
- 实例

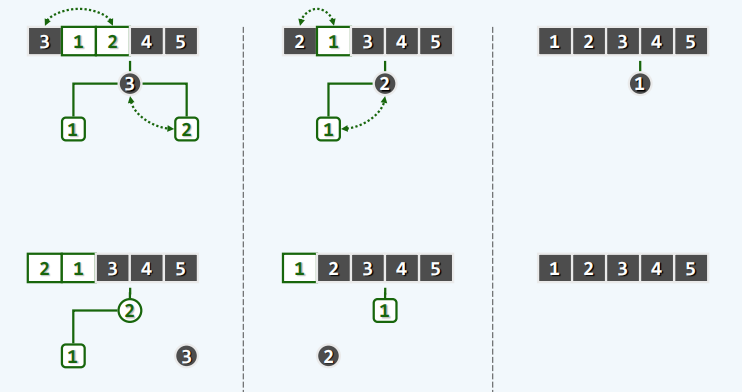
就地堆排序
-
原理

-
实现
//堆排序
public void heapSort(T[] A,int lo,int hi){
copyFrom(A,lo,hi);
int n = hi - lo;
heapify(n);
while (0 < --n){
swap(A[0],A[n]);
percolateDown(n,0);
}
}
- 实例

左视堆
概念
对于堆的合并来说,可以想到的有两种方法:
-
简单的取出并插入
-
将两个堆中词条视为无顺序的,用堆合并

-
堆不需要与二叉树一样保持平衡
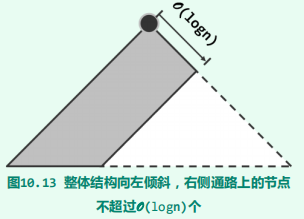
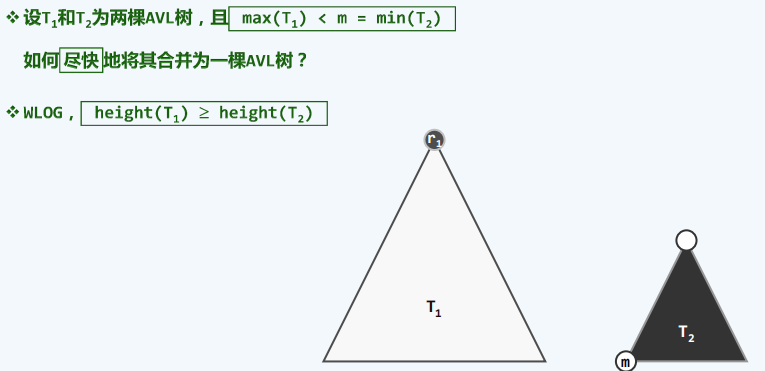
左视堆:左式堆是优先级队列的另一实现方式,可高效地支持堆合并操作。其基本思路是:在保持堆序性的前提下附加新的条件,使得在堆的合并过程中,只需调整很少量的节点。具体地,需参与调整的节点不超过O(logn)个,故可达到极高的效率。
模板类
使用的是二叉树结构
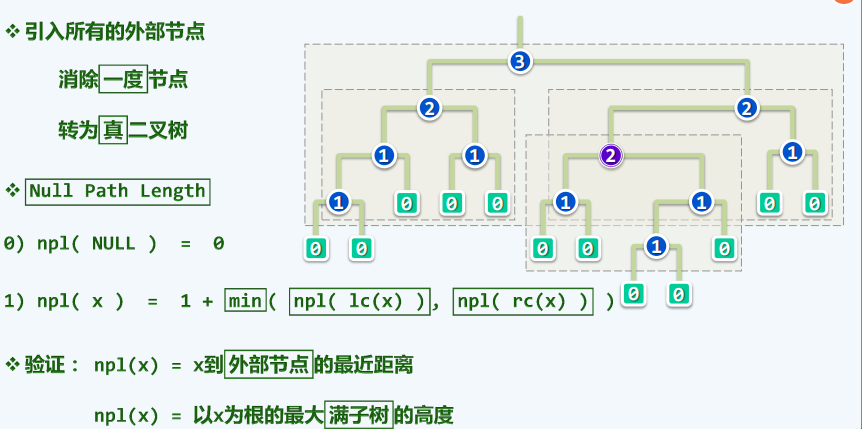
空节点路径长度

左倾性

最右侧通路

package com.atguigu.domin;
import com.atguigu.self.BinNode;
import com.atguigu.self.BinTree;
/**
* @anthor shkstart
* @create 2020-08-13 15:07
*/
public class PQ_LeftHeap<T> extends BinTree<T> implements PQ<T> {
@Override
public void insert(T e) {
//插入元素
BinNode<T> v = new BinNode<T>(e);
_root = merge(_root,v);
_root.parent = null;
_size++;
}
@Override
public T getMax() {
//取出优先级最高的元素
return _root.data;
}
@Override
public T delMax() {
//删除优先级最高的元素
BinNode<T> lHeap = _root.lc;
//左子堆
BinNode<T> rHeap = _root.rc;
//右子堆
T e = _root.data;
//备份堆顶处的最大元素
_size--;
//删除一个节点
_root = merge(lHeap,rHeap);
//原左右堆合并
if (_root != null){
//更新父子链接
_root.parent = null;
}
return e;
//返回源节点处数据
}
public BinNode<T> merge(BinNode<T> a, BinNode<T> b){
if (a ==null) return b;
if (b == null) return a;
if (lt(a.data,b.data)) swap(b,a);
a.rc = merge(a.rc,b);
a.rc.parent = a;
if (a.rc == null || a.rc.npl < a.rc.npl){
swap(a.lc,a.rc);
}
a.npl = (a.rc != null) ? a.rc.npl + 1:1;
return a;
}
//一些必要的方法
void swap(BinNode<T> a,BinNode<T> b){
BinNode<T> c = a;
a = b;
b = c;
}
Boolean lt(T a,T b){
return ((int)a < (int)b);
}
}
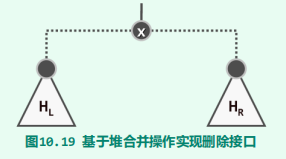
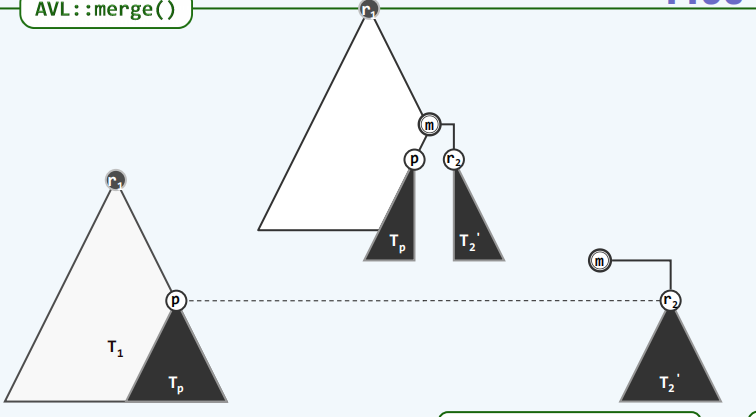
合并
- 原理
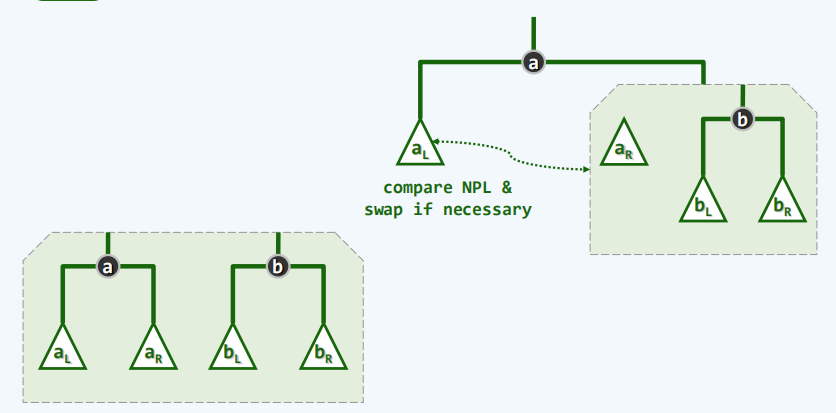

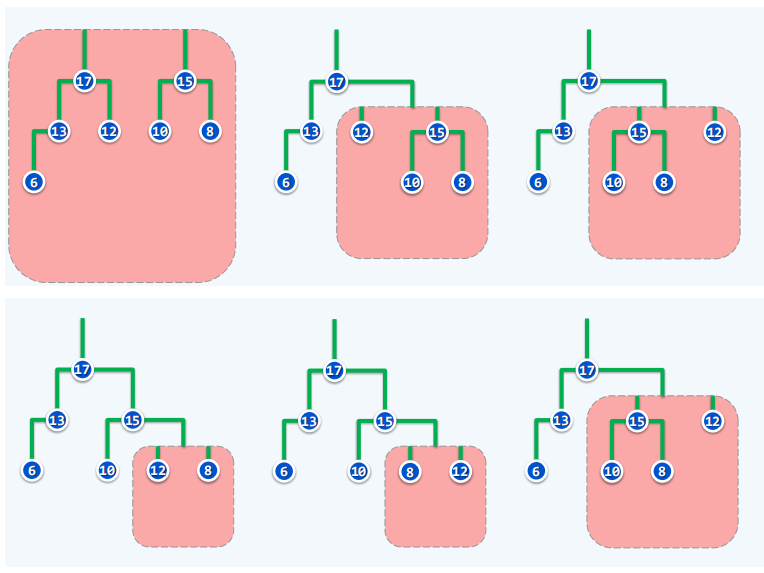
- 实现
public BinNode<T> merge(BinNode<T> a, BinNode<T> b){
if (a ==null) return b;
if (b == null) return a;
if (lt(a.data,b.data)) swap(b,a);
a.rc = merge(a.rc,b);
a.rc.parent = a;
if (a.rc == null || a.rc.npl < a.rc.npl){
swap(a.lc,a.rc);
}
a.npl = (a.rc != null) ? a.rc.npl + 1:1;
return a;
}
//一些必要的方法
void swap(BinNode<T> a,BinNode<T> b){
BinNode<T> c = a;
a = b;
b = c;
}
Boolean lt(T a,T b){
return ((int)a < (int)b);
}
- 实例
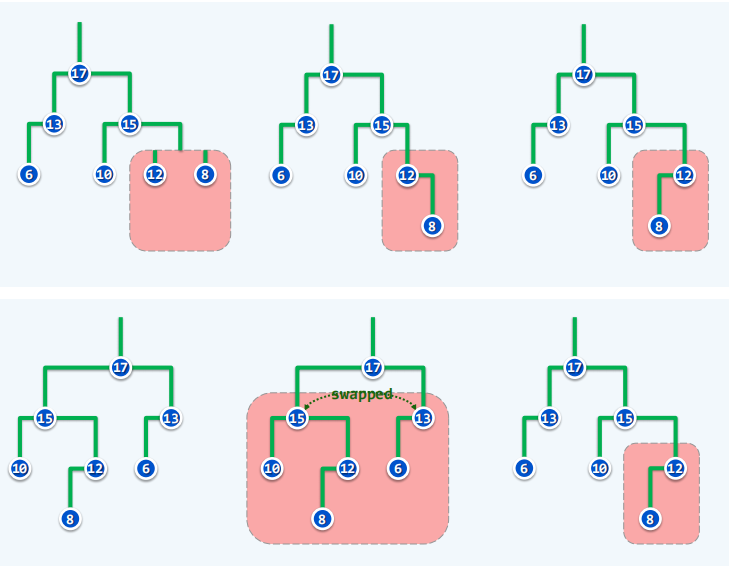
基于合并的插入和删除
- 原理
- 实现
@Override
public void insert(T e) {
//插入元素
BinNode<T> v = new BinNode<T>(e);
_root = merge(_root,v);
_root.parent = null;
_size++;
}
@Override
public T getMax() {
//取出优先级最高的元素
return _root.data;
}
@Override
public T delMax() {
//删除优先级最高的元素
BinNode<T> lHeap = _root.lc;
//左子堆
BinNode<T> rHeap = _root.rc;
//右子堆
T e = _root.data;
//备份堆顶处的最大元素
_size--;
//删除一个节点
_root = merge(lHeap,rHeap);
//原左右堆合并
if (_root != null){
//更新父子链接
_root.parent = null;
}
return e;
//返回源节点处数据
}
- 实例
锦标赛排序
原始算法
-
原理
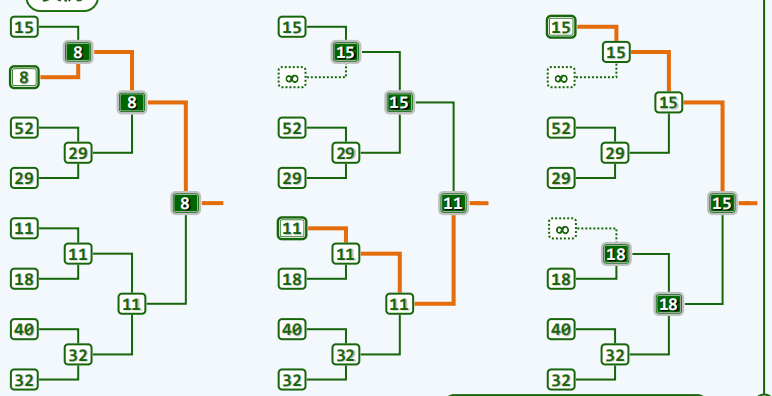
-
实现
相关链接
https://www.cnblogs.com/binarylei/p/10115921.html#24-堆排序-vs-快速排序
package com.atguigu.domin;
/**
* @anthor shkstart
* @create 2020-08-13 16:31
*/
public class TourSort extends PQ_CompHeap{
public static final int MAX = 10000;
private class Node//用node来存储竞赛排序过程中的节点,包括里面的数据和数据在数组中的ID
{
public int data;
public int id;
public Node()
{
}
public Node(int data, int id) {
this.data = data;
this.id = id;
}
}
public void Adjust(Node[] B, int idx){
//当去除最小元素以后,我们要调整数组
while (idx != 0){
if (idx / 2 == 0){
if (B[idx].id == -1){
B[Parent(idx)] = B[idx + 1];
} else {
B[Parent(idx)] = B[idx].data > B[idx+1].data ? B[idx+1] : B[idx];
}
} else {
if (B[idx].id == -1){
B[Parent(idx)] = B[idx - 1];
} else {
B[Parent(idx)] = B[idx].data > B[idx-1].data ? B[idx-1] : B[idx];
}
}
}
}
public void creat(int[] A) {
int n = 1;
while (n < A.length){
n *= 2;
}
int s = n - 1;
Node[] B = new Node[2*n - 1];
for (int i = 0;i < n;i++){
if (i < A.length){
B[n - 1 + i].data = A[i];
B[n - 1 + i].id =n - 1 + i;
} else {
B[n - 1 + i].data = MAX;
B[n - 1 + i].id = -1;
}
}
while (--s >= 0){
if (B[LChild(s)].id == (-1)) {
B[s] = B[RChild(s)];
} else if (B[RChild(s)].id == (-1)) {
B[s] = B[LChild(s)];
} else {
B[s] = (B[LChild(s)].data < B[RChild(s)].data) ? B[LChild(s)] : B[RChild(s)];
}
}
for ( int i = 0; i < A.length; i++)//实际排序的过程
{
A[i] = B[0].data;
//取出最小的
B[B[0].id].id = -1;
Adjust(B, B[0].id);
}
}
}
改进算法
-
原理
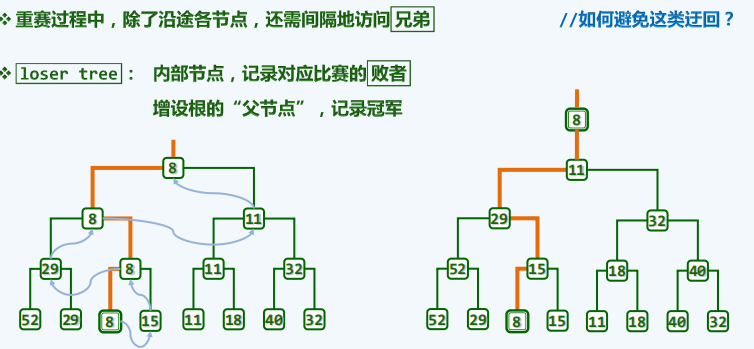
-
实现(还未写)
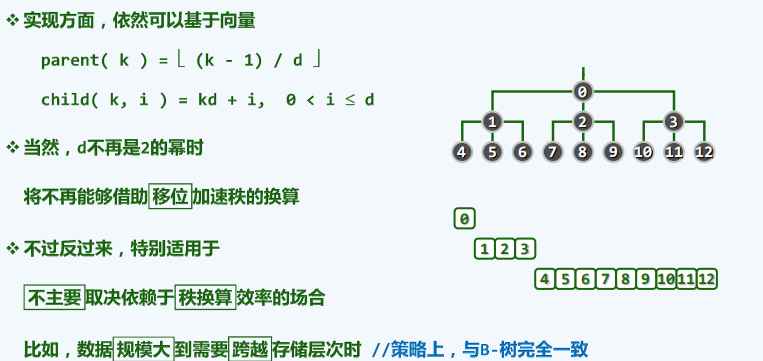
多叉堆
-
原理
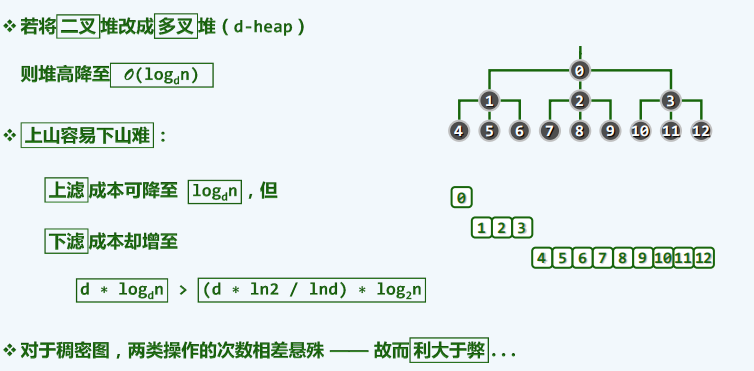
-
效率

- 实现(还未写)