本博文意在巩固基础知识,高手请绕过。部分代码和内容参考严蔚敏人民邮电版出版社《数据结构》
树和二叉树
树
树(tree)是n(n≥0)个结点的有限集T,在任意一棵非空树中:
有且仅有一个特定的结点,称为树的根(root),
当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1,T2,……Tm,其中每一个集合本身又是一棵树,称为根的子树
树的特点:
非空树中至少有一个结点 —— 根
树中各子树是互不相交的集合
树的基本术语:
结点(node)——表示树中的元素,包括数据项及若干指向其子树的分支
结点的度(degree)——结点拥有的子树数
叶子(leaf)——度为0的结点
双亲(parents)——孩子结点的上层结点叫该结点的双亲
兄弟(sibling)——同一双亲的孩子
树的度——一棵树中最大的结点度数
结点的层次(level)——从根结点算起,根为第一层,它的孩子为第二层……
深度(depth)——树中结点的最大层次数
森林(forest)——m(m³0)棵互不相交的树的集合
二叉树
二叉树是一种特殊的树
定义:二叉树是n(n³0)个结点的有限集,它或为空树(n=0),或由一个根结点和两棵分别称为左子树和右子树的互不相交的二叉树构成
特点:
每个结点至多有2 棵子树(即不存在度大于2的结点);
二叉树的子树有左、右之分,且其次序不能任意颠倒。
二叉树的5种基本形态:
空二叉树
只有根结点的二叉树
右子树为空
左子树为空
左、右子树均非空
二叉树性质
性质1:在非空二叉树中,第i层上至多有2i-1个结点(i≧1)
性质2:深度为k的二叉树至多有2k-1个结点(k≧1)
性质3:对任何一棵二叉树,若其叶子结点数为n0,度为2的结点数为n2,则n0=n2+1
性质4:n个结点的完全二叉树深度为:ë㏒2nû +1。
其中符号: ëxû表示不大于x的最大整数。éxù 表示不小于x的最小整数。
性质5:若对一棵有n个结点的完全二叉树(深度为└㏒2n┘+1)的结点按层(从第1层到第ë㏒2nû +1层)序自左至右进行编号,则对于编号为i(1≦i≦n)的结点:
⑴ 若i=1:则结点i是二叉树的根,无双亲结点;否则,若i>1,则其双亲结点编号是 ëi/2û 。
⑵ 如果2i>n:则结点i为叶子结点,无左孩子;否则,其左孩子结点编号是2i。
⑶ 如果2i+1>n:则结点i无右孩子;否则,其右孩子结点编号是2i+1。
满二叉树
一棵深度为k且有2k-1个结点的二叉树称为满二叉树。
完全二叉树
如果深度为k,由n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1到n的结点一一对应,该二叉树称为完全二叉树。或深度为k的满二叉树中编号从1到n的前n个结点构成了一棵深度为k的完全二叉树。
遍历二叉树
三种遍历方式
1.DLR——先(根)序遍历。
2.LDR——中(根)序遍历。
3.LRD——后(根)序遍历。
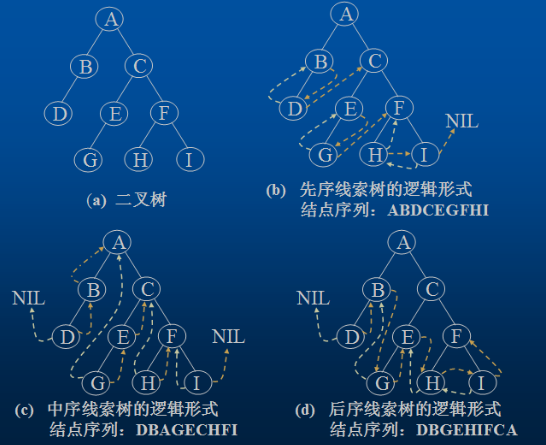
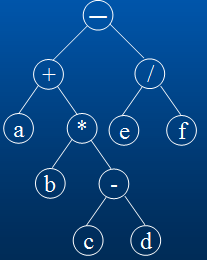
如下图所示的二叉树表示表达式:(a+b*(c-d)-e/f)
按不同的次序遍历此二叉树,将访问的结点按先后次序排列起来的次序是:
其先序序列为: -+a*b-cd/ef
其中序序列为: a+b*c-d-e/f
其后序序列为: abcd-*+ef/-
树的遍历
树的遍历可以先转化为二叉树,然后进行遍历。
树的遍历有三种:
1.先根(序)遍历:若树不空,则先访问根结点,然后依次先根遍历各棵子树。
2.后根(序)遍历:若树不空,则先依次后根遍历各棵子树,然后访问根结点。
3.按层次遍历:若树不空,则自上而下自左至右访问树中每个结点。
森林的遍历有两种:
1.先序遍历(对森林中的每一棵树进行先根遍历)
若森林不空,则访问森林中第一棵树的根结点;
先序遍历森林中第一棵树的子树森林;
先序遍历森林中(除第一棵树之外)其余树构成的森林。
2.中序遍历(对森林中的每一棵树进行后根遍历)
若森林不空,则中序遍历森林中第一棵树的子树森林;
访问森林中第一棵树的根结点;
中序遍历森林中(除第一棵树之外)其余树构成的森林。
哈夫曼树
假设n个权值(w1…… wn),试构造一棵有n个叶子结点的二叉树,每个叶子结点权是wi,则其中带权路径长度WPL最小的二叉树称作最优二叉树,也称为哈夫曼树。
一般情况下,最优二叉树中,权值越大的叶子离根越近。
构造哈夫曼树的方法 ——哈夫曼算法
假设有n个权值分别为 w1,w2,…,wn, 则构造出的哈夫曼树有n个叶子结点。n个权值则哈夫曼树的构造规则为:
(1) 将这n个结点看作是n 棵单结点二叉树,结点的权值分别是w1, w2, …, wn ;这n棵二叉树构成一个二叉树的集合M。
(2) 在集合M中选出两个根结点的权值最小的二叉树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3) 从集合M中删除选取的两棵二叉树,并将新树加入该集合
(4) 重复(2)、(3)步,直到集合M中只剩一棵二叉树为止,该二叉树即为我们所求得的哈夫曼树。
哈夫曼编码方法
以字符集C作为叶子结点,次数或频度集W作为结点的权值来构造哈夫曼树。规定哈夫曼树中左分支代表“0”,右分支代表“1” 。
从根结点到每个叶子结点所经历的路径分支上的“0”或“1”所组成的字符串,为该结点所对应的编码,称之为哈夫曼编码。