Integer Partition
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 169 Accepted Submission(s): 79
Problem Description
Given n, k, calculate the number of different (unordered) partitions of n such that no part is repeated k or more times.
Input
First line, number of test cases, T. Following are T lines. Each line contains two numbers, n and k.
1<=n,k,T<=105
1<=n,k,T<=105
Output
T lines, each line contains answer to the responding test case. Since the numbers can be very large, you should output them modulo 109+7.
Sample Input
4
4 2
4 3
4 4
4 5
Sample Output
2
4
4
5
Source
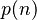 的生成函数是
的生成函数是
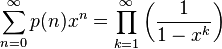 (1)
(1)- 再
利用五边形数定理可得到以下的展开式:
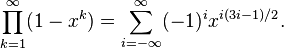 (2)
(2)- 将(2)式带入(1)式,并乘到(1)式的左边,进行展开,合并同类项,根据非常数项的系数为0!!
- 即将
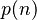 生成函数配合五边形数定理,可以得到以下的递归关系式
生成函数配合五边形数定理,可以得到以下的递归关系式
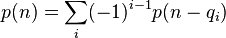
- 以上就可以把
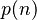 求出来了,接下来就来看看本题与之有什么联系呢?
求出来了,接下来就来看看本题与之有什么联系呢? - 首先我们可以写出本题的母函数
- Σf(n)xˆn=(1+x+x^2+..+x^(k-1))*(1+x^2+x^4+..+x^2(k-1))*..*(1+x^n+..+x^n(k-1));(题目中说 no part is repeated k or more times)
- =(1-x^k)*(1-x^2k)*...*(1-x^nk)/((1-x)*(1-x^2)*....*(1-x^n);
- =(1-x^k)*(1-x^2k)*...*(1-x^nk)*Σp(n)xˆn;
- 对于(1-x^k)*(1-x^2k)*...*(1-x^nk),可令x^k=y;再利用五边形定理将其打开;
- 之后就简单啦!!自己搞一下吧!!
-
 View Code
View Code1 #include<stdio.h> 2 typedef __int64 ll; 3 const int mo=1000000007; 4 int p[100010]; 5 void pre() 6 { 7 p[0]=1; 8 for(int i=1;i<=100000;i++) 9 { 10 int t=1,ans=0,kk=1; 11 while(1) 12 { 13 int tmp1,tmp2; 14 tmp1=(3*kk*kk-kk)/2; 15 tmp2=(3*kk*kk+kk)/2; 16 if(tmp1>i)break; 17 ans=(ll)(ans+(ll)t*p[i-tmp1]+mo)%mo; 18 if(tmp2>i)break; 19 ans=(ll)(ans+(ll)t*p[i-tmp2]+mo)%mo; 20 t=-t; 21 kk++; 22 } 23 p[i]=ans; 24 } 25 } 26 ll work(int n,int k) 27 { 28 int i,j; 29 ll ans; 30 ans=p[n]; 31 int t=1,kk=1; 32 while(1) 33 { 34 t=-t; 35 ll tmp1,tmp2; 36 tmp1=(ll)k*(3*kk*kk-kk)/2; 37 tmp2=(ll)k*(3*kk*kk+kk)/2; 38 if(tmp1>n)break; 39 ans=(ans+t*p[n-tmp1]+mo)%mo; 40 if(tmp2>n)break; 41 ans=(ans+t*p[n-tmp2]+mo)%mo; 42 kk++; 43 } 44 return ans; 45 } 46 int main() 47 { 48 pre(); 49 int T,n,k; 50 scanf("%d",&T); 51 while(T--) 52 { 53 scanf("%d%d",&n,&k); 54 ll ans=work(n,k); 55 printf("%I64d ",ans); 56 } 57 }
