数论
数论要写起来真是写不完了...不如先看题？
非常无聊不知道该干什么的时候就过来补一些数论知识吧。
学到了一些简便的写法：
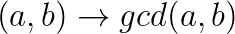
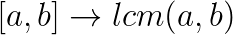
费马小定理：$a^{p-1}equiv 1(\%p)$,p是质数，a不等于p。其实这也是欧拉定理的一种特例；
欧拉定理：
·
这个东西叫做欧拉函数，表示小于等于i的正整数中与i互质的数的个数。
·
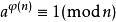$gcd(a,n)=1$
·
·
·
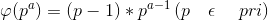
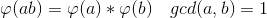
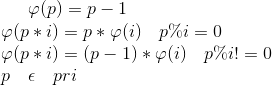
·因为欧拉函数种种美妙的性质，可以在线性筛素数的同时也筛出每个数的欧拉函数来呢。
向量：https://www.luogu.org/problemnew/show/P2520
今天讲数论提到这个题，突然发现...我还没做过，被asuldb大佬嘲讽了一番，发愤图强还是做掉了这个题。
题意概述：给定$(a,b),(a,-b),(-a,b),(-a,-b),(b,a),(b,-a),(-b,a),(-b,-a)$,随便拼，问能不能拼出来$(x,y)$。说明：这里的拼就是使得你选出的向量之和为$(x,y)$
这句说明真是良心，要是没有我还以为是什么计算几何毒瘤题呢.
观察发现，用一些向量可以拼凑出$(2a,0)(2b,0)(-2a,0)(-2b,0)(0,2a)(0,2b)(0,-2a)(0,-2b)$这些优美的好向量。好在哪里？因为只影响一个不影响另一个，所以可以拿过来就随便拼，不用考虑对另一个的影响。但是只用这些东西拼是肯定不行的，毕竟可能$x$正好等于$3a$呢？如果可行，$x$肯定可以被表示成一些$a$的和加上一些$b$的和，而这些$a$可以表示成一些$2a$加上一个或零个$a$，$b$同理。但是加一个$a$可不是这么简单的，它是一定会影响$y$的，所以不能随便加。观察思考发现，除了上述那些优美向量，其实最多只可能再加一个$(a,b)$向量或是$(b,a)$向量，当然也可以各加一个，为什么不用尝试(-a,b)向量这些呢？因为如果我们已经试过了$(a,b)$这个却不行，那说明$X+a$不能用优美向量拼出来，因为我们有一个$(2a,0)$的向量，所以$X-a$必然也是不行的~ 其他的也都同理。现在只需要枚举这两个向量的使用情况就可以得到答案。解两个扩欧方程:$$2ax_1+2by_1=X$$ $$2ax_2+2by_2=Y$$,如果有解就行。但是不用真的去算这个方程，只要用判断扩欧是否有解的方法判一下就行。
1 # include <cstdio> 2 # include <iostream> 3 4 using namespace std; 5 6 int T; 7 bool f; 8 long long g,a,b,x,y; 9 10 long long gcd (long long a,long long b) 11 { 12 return b?gcd(b,a%b):a; 13 } 14 15 int main() 16 { 17 cin>>T; 18 while (T--) 19 { 20 scanf("%lld%lld%lld%lld",&a,&b,&x,&y); 21 f=false; 22 if(a<0) a=-a; 23 if(b<0) b=-b; 24 g=gcd(2*a,2*b); 25 if(x%g==0&&y%g==0) f=true; 26 x+=b,y+=a; 27 if(x%g==0&&y%g==0) f=true; 28 x+=a,y+=b; 29 if(x%g==0&&y%g==0) f=true; 30 x=x-b,y=y-a; 31 if(x%g==0&&y%g==0) f=true; 32 if(f) printf("Y "); 33 else printf("N "); 34 } 35 return 0; 36 }
小凯的疑惑：https://www.luogu.org/problemnew/show/P3951
题意概述：小学奥数？
这里是一个瞎搞做法，面向excel编程。
首先把$a$换成其中较小的那个数字,把所有的数字按照$a$个一行的顺序排出来,举个例子:a=3,b=5;
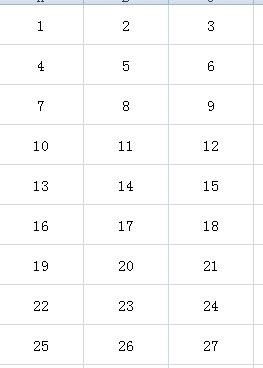
然后就可以枚举$a$的使用数量,首先用零个,穷举$b$的使用数量,不用算特别多,先填上5`6行就可以：
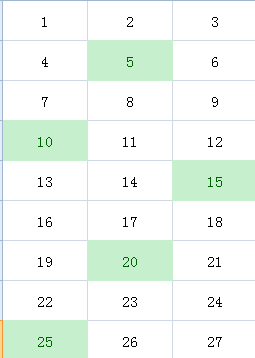
这时候我们发现这些绿色块的排列方式有一定规律，就像这样：
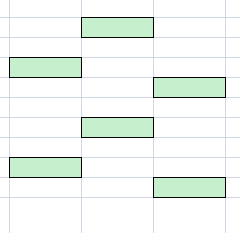
先不要在乎这个规律，此时选$1$个$a$,接着涂色：
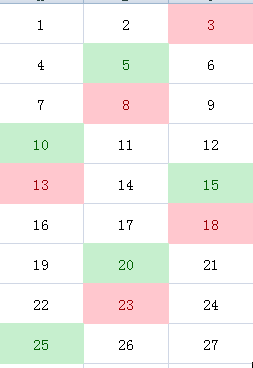
这时候发现红色的块不就是绿色往下平移一格嘛...
现在可以大胆猜想（其实也不是猜想），随着$a$使用越来越多，色块就是不断的向下平移，所以第一次涂的那些块正上方的那些块永远也涂不到了。那么答案一定就在第一次涂到的那些块中的某一个的正上方一个！所以在出现循环之前，一共涂了多少个绿色的块呢？其实就是$a$个，但是其中有一个正好是$a*b$,那个是不能要的,因为它上面的那些块都是$a$的倍数.这样就有(a-1)个块了,这些块中,哪个最靠下呢?当然是除了$ab$以外最下排那一个了...这个块在哪里呢?就在$b*(a-1)$那里，它上面的那一块自然就是$b*(a-1)-a=a*b-a-b$,做过这道题的同学当然知道这就是正确答案了,但是还有一个疑惑没有解决,那就是会不会在涂上这一块之前就已经有某一个$b$的倍数出现在这一列上了?答案是否定的,这里要用到剩余系的一个定理，但是不用担心，我们今天不提什么剩余系（因为我也不会).到这里大家就可以点击右上角离开啦!
不过我想到了一个神奇的证明方法!假设有两个点真的涂到了同一列上,且都在$ab$那一行的上方,那么设它们为$qb,pb(p<q<a)$,因为涂数的列数等价于$bk\%a$的数字,所以有:
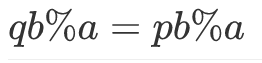
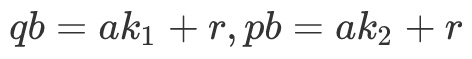
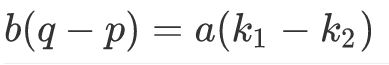
此时$b$的某次方等于$a$的某次方，这种时候，因为都是整数，所以等式两边的数一定都是$[a,b]$的倍数.因为$(a,b)=1$,所以$[a,b]=a*b$
所以就有
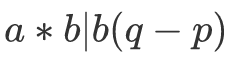
这时候就出现问题了...$q,p$本身都是小于$a$的,可是它们两个的差竟然成a的倍数了?由此可知假设不成立,所以$ab$以上的每一列有且仅有一个数字,绝对不会出现两个数在一列的情况。完美的结束了。
题意概述:给定一个长度为$n$的数列${ a_i}$,求一个 $x$ 使得 $sum_{i=1}^{n}frac{a_i}{x}+a_i \% x$ 最小. 注：分数形式表示整除.
首先可以发现这个 $x$ 不会比 $max { a_i}$ 更大,所以可以枚举 $x$ 后暴力计算这个式子,复杂度 $O(max { a_i} imes n)$
化一化式子:$sum_{i=1}^n (frac{a_i}{x} + a- frac{a_i}{x} imes x)=sum_{i=1}^n (a +(1-x) imes frac{a_i}{x})$
枚举 $frac{a_i}{x}$ 的取值，可以直接计算满足条件的取值区间，统计有多少个 $a_i$ 满足这个条件；取值的范围不会超过 $frac{max {a_i}}{x}$，因为$sum_{i=1}^n frac{n}{i} approx logN$，所以总复杂度就是$O(NlogN)$
1 # include <cstdio> 2 # include <iostream> 3 # include <algorithm> 4 # define R register int 5 # define ll long long 6 7 using namespace std; 8 9 const int maxn=1000006; 10 int n,m; 11 int x,s[maxn]; 12 ll ans,sol,S; 13 14 int main() 15 { 16 scanf("%d",&n); 17 for (R i=1;i<=n;++i) scanf("%d",&x),S+=x,s[ x ]++,m=max(m,x); 18 for (R i=1;i<=m;++i) s[i]+=s[i-1]; 19 sol=S; 20 for (R i=2;i<=m;++i) 21 { 22 ans=S; 23 for (R j=1;i*j<=m;++j) 24 ans-=(1LL*s[min(m,i*(j+1)-1)]-s[i*j-1])*1LL*(i-1)*j; 25 sol=min(ans,sol); 26 } 27 printf("%lld",sol); 28 return 0; 29 }
---shzr