矩阵的定义

矩阵的运算(含幂运算)
加减比较简单,就是对应元素相加减 (只有行列都相同的矩阵才可以进行)
用NumPy 来演示一下矩阵加法
Numpy有专门的矩阵函数(np.mat)
import numpy as np
# 创建两个集合
A = np.arange(1,10).reshape((3,3))
B = np.arange(9).reshape((3,3))
print(A)
print("-"*5)
print(B)
输出
[[1 2 3] [4 5 6] [7 8 9]] ----- [[0 1 2] [3 4 5] [6 7 8]]
A + B
输出:
array([[ 1, 3, 5],
[ 7, 9, 11],
[13, 15, 17]])
A - B
输出:
array([[1, 1, 1],
[1, 1, 1],
[1, 1, 1]])
# 之前说过 ”只有行列都相同的矩阵才可以进行“ 来验证一下
# 创建一个2行3列的矩阵
C = np.arange(6).reshape((2,3))
D = np.arange(6).reshape((3,2))
print(C)
print("-"*5)
print(D)
输出:
[[0 1 2] [3 4 5]] ----- [[0 1] [2 3] [4 5]]
C + D # 不同形状的矩阵不能进行加运算
输出:
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-8-bc97e29f7e31> in <module>()
1 # 2行3列的矩阵 + 3行2列的矩阵
----> 2C + D # 不同形状的矩阵不能进行加运算
.数乘、数除
这个也比较简单,就是和每个元素相乘,eg:2×A,A原本的每一个元素都扩大了两倍
数除其实就是乘以倒数(1/x)
print(A)
[[1 2 3] [4 5 6] [7 8 9]]
2 * A
array([[ 2, 4, 6],
[ 8, 10, 12],
[14, 16, 18]])
A / 2
array([[0.5, 1. , 1.5],
[2. , 2.5, 3. ],
[3.5, 4. , 4.5]])
.矩阵乘法

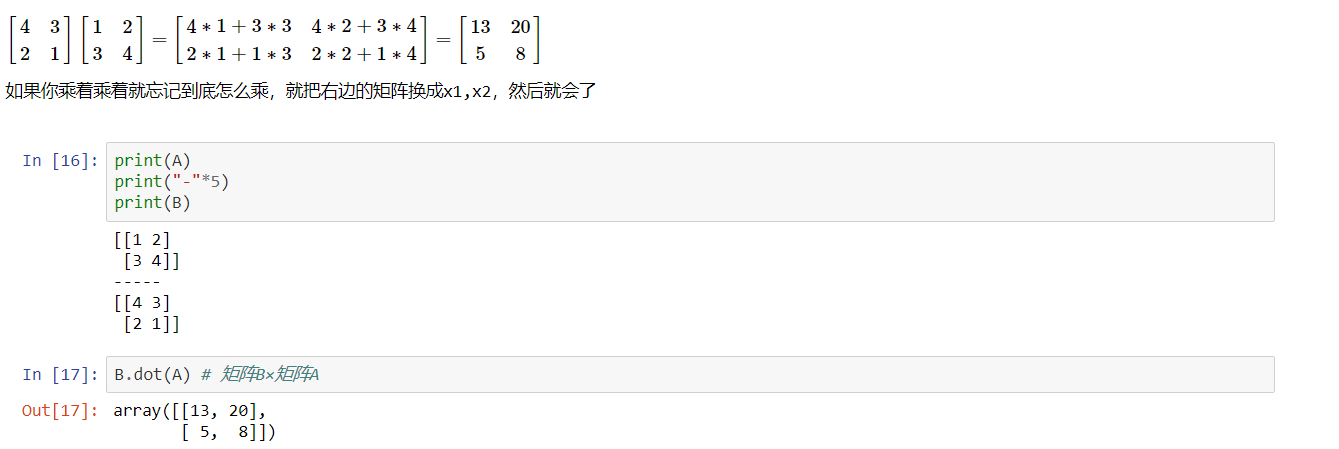
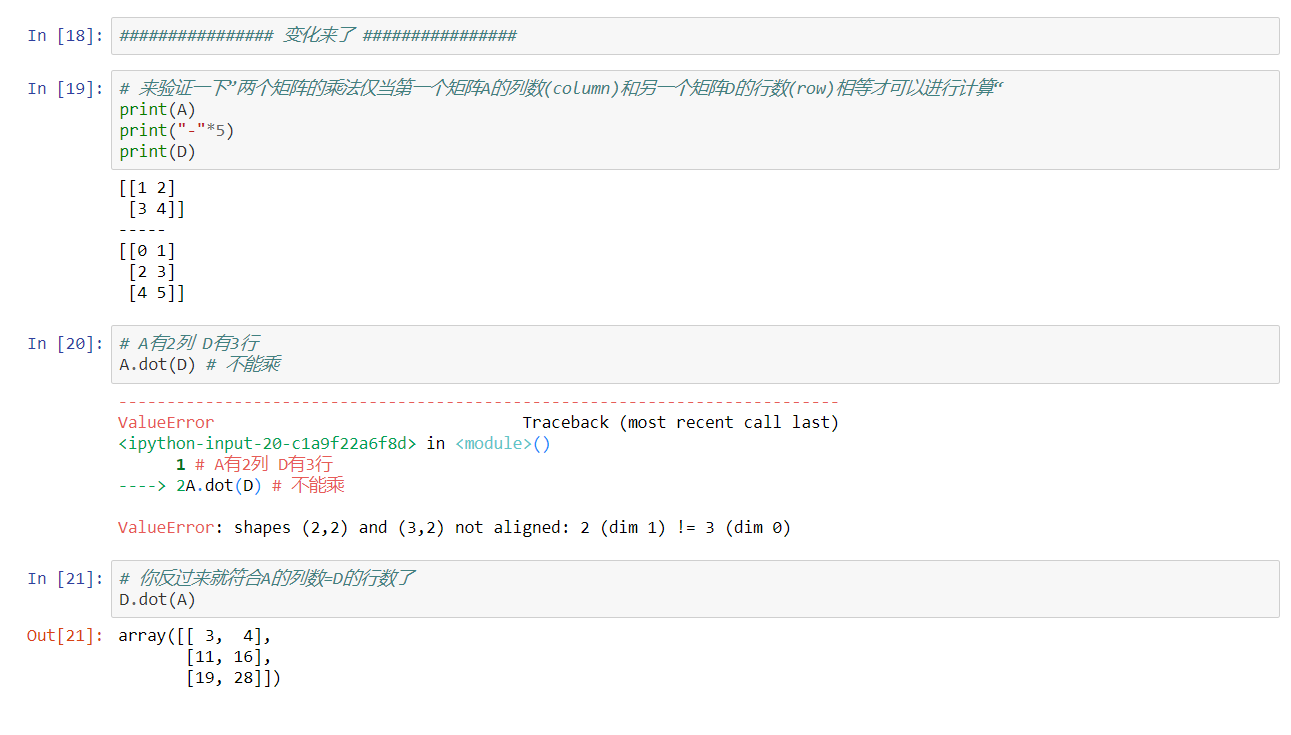
两个矩阵的乘法仅当第一个矩阵A的列数(column)和另一个矩阵B的行数(row)相等才可以进行计算


程序验证了我们上面的运算结果,还得注意一下:
A×B和B×A是不一样的,eg:B×A
.幂乘、幂运算
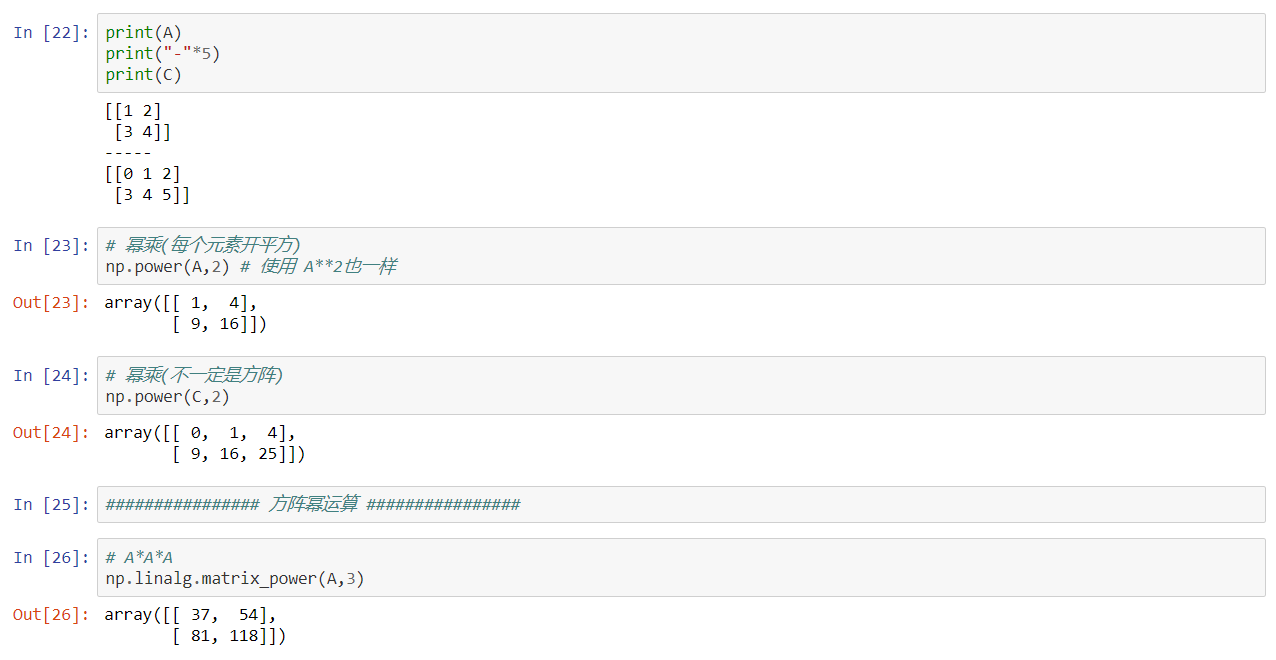
幂乘比较简单,就是每个元素开平方,不一定是方阵
必须是方阵才能进行幂运算,比如A²=A×A(矩阵相乘前提:第一个矩阵A的行=第二个矩阵A的列==>方阵)

来个小结 + 扩展:
矩阵的加法运算满足交换律:A + B = B + A
矩阵的乘法满足结合律和对矩阵加法的分配律:
结合律:(AB)C = A(BC)
左分配律:(A + B)C = AC + BC
右分配律:C(A + B) = CA + CB
矩阵的乘法与数乘运算之间也满足类似结合律的规律;与转置之间则满足倒置的
分配律:c(A + B) = cA + cB
结合律:c(AB) = (cA)B = A(cB)
矩阵乘法不满足交换律 一般来说,矩阵A及B的乘积AB存在,但BA不一定存在,即使存在,大多数时候AB ≠ BA
.特殊矩阵

import numpy as np
# 一维
# 可以指定类型 np.zeros(5,dtype=int)
print(np.zeros(5)) # 完整写法:np.zeros((5,))
print("********************
")
# 二维
print(np.zeros((2,5)))# 建议用元组,官方文档都是元组
print("********************
")
# 三维 ==> 可以这么理解,2个2*5(2行5列)的矩阵
print(np.zeros((2,2,5)))
print("********************
")
# `np.ones(tuple)` 用法和`np.zeros(tuple)`差不多
# 可以指定类型 np.ones(5,dtype=int)
# 一维
print(np.ones(5)) # 完整写法 np.ones((5,))
print("********************
")
# 二维,传一个shape元组
print(np.ones((2,5)))
print("********************
")
# 三维 可以理解为两个二维数组
print(np.ones((2,2,5)))
print("********************
")
################ 指定值矩阵 ################
# 创建指定值的矩阵:
print(np.full((3,5),222))
print("********************
")
# 创建指定值的矩阵,浮点类型
print(np.full((3,5),222.0))
print("********************
")
输出:
[0. 0. 0. 0. 0.]
********************
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
********************
[[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]]
********************
[1. 1. 1. 1. 1.]
********************
[[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]]
********************
[[[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]]
[[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]]]
********************
[[222 222 222 222 222]
[222 222 222 222 222]
[222 222 222 222 222]]
********************
[[222. 222. 222. 222. 222.]
[222. 222. 222. 222. 222.]
[222. 222. 222. 222. 222.]]
********************
转置矩阵
转置矩阵 :将矩阵的行列互换得到的新矩阵(行列式不变)
m行×n列的矩阵行和列交换后就变成了n行×m列的矩阵,eg:3行×2列 ==> 2行×3列

再次提醒:两个矩阵的乘法仅当第一个矩阵A的列数(column)和另一个矩阵B的行数(row)相等才可以进行计算
import numpy as np
A = np.arange(6).reshape((2,3))
print("
A:
",A)
# 转置矩阵(行列互换)
A.T
print("
A.T:
",A.T)
B = np.random.randint(10,size=(2,3))
print("
B:
",B)
print("-"*5)
print("
B.T:
",B.T)
################ 验证系列 ################
# 验证一下(A+B)^T=A^T+B^T
print("
A.T + B.T:
",A.T + B.T)
print("-"*5)
print("
(A+B).T:
",(A+B).T)
# 验证一下(A+B)^T=A^T+B^T
# 其实也再一次验证了,Numpy运算符默认是对每一个元素的操作
print("
(A+B).T == A.T + B.T:
",(A+B).T == A.T + B.T)
# 把A变成3*2的矩阵,不够元素用0补
# reshape:有返回值,不对原始多维数组进行修改
# resize:无返回值,会对原始多维数组进行修改
A.resize(3,2)
print("
B:
",B)
print("
A:
",A)
print("
np.power(A,3):
",np.power(A,3))
# A*A*A
C=np.arange(1,5).reshape(2,2)
D=np.linalg.matrix_power(C,3)
print("
C:",C)
print("
D:",D)
A:
[[0 1 2]
[3 4 5]]
A.T:
[[0 3]
[1 4]
[2 5]]
B:
[[3 1 8]
[5 4 8]]
-----
B.T:
[[3 5]
[1 4]
[8 8]]
A.T + B.T:
[[ 3 8]
[ 2 8]
[10 13]]
-----
(A+B).T:
[[ 3 8]
[ 2 8]
[10 13]]
(A+B).T == A.T + B.T:
[[ True True]
[ True True]
[ True True]]
B:
[[3 1 8]
[5 4 8]]
A:
[[0 1]
[2 3]
[4 5]]
np.power(A,3):
[[ 0 1]
[ 8 27]
[ 64 125]]
C: [[1 2]
[3 4]]
D: [[ 37 54]
[ 81 118]]
上三角矩阵和下三角矩阵

import numpy as np
# 创建一个5行4列矩阵
A = np.random.randint(10,size=(4,4))
print("
A:
",A)
# 上三角
np.triu(A)
print("
np.triu(A):
",np.triu(A))
# 下三角
np.tril(A)
print("
np.tril(A):
",np.tril(A))
# 验证一下最后一个性质
# 三角矩阵的逆矩阵也仍然是三角矩阵
print("
np.triu(A).T:
",np.triu(A).T)
print('-'*5)
print("
np.tril(A).T:
",np.tril(A).T)
A:
[[9 9 5 7]
[0 4 6 6]
[1 4 9 7]
[2 4 5 2]]
np.triu(A):
[[9 9 5 7]
[0 4 6 6]
[0 0 9 7]
[0 0 0 2]]
np.tril(A):
[[9 0 0 0]
[0 4 0 0]
[1 4 9 0]
[2 4 5 2]]
np.triu(A).T:
[[9 0 0 0]
[9 4 0 0]
[5 6 9 0]
[7 6 7 2]]
-----
np.tril(A).T:
[[9 0 1 2]
[0 4 4 4]
[0 0 9 5]
[0 0 0 2]]
对角矩阵

import numpy as np
# 简单创建
A=np.diag([3,9,6])
print("
A:
",A)
B=np.diag([2,2,2])
print("
B:
",B)
# 获取对角元素,然后再生成对角矩阵
C= np.random.randint(10,size=(4,4))
D = np.diag(C.diagonal()) #或者 np.diag(np.diag(A))
print("
C:
",C)
print("
D:
",D)
# 对角矩阵的矩阵幂运算等于其对应元素的幂运算 D**3
E=D.dot(D).dot(D)
print("
E:
",E)
A:
[[3 0 0]
[0 9 0]
[0 0 6]]
B:
[[2 0 0]
[0 2 0]
[0 0 2]]
C:
[[6 6 0 7]
[5 9 1 4]
[9 1 1 0]
[5 0 6 9]]
D:
[[6 0 0 0]
[0 9 0 0]
[0 0 1 0]
[0 0 0 9]]
E:
[[216 0 0 0]
[ 0 729 0 0]
[ 0 0 1 0]
[ 0 0 0 729]]
.单位矩阵

#定义一个2行的单位矩阵(列默认和行一致)
# np.eye(rows,columns=rows)
A=np.eye(2)
print("
A:
",A)
# 可以指定类型
B = np.eye(4,dtype=int)
print("
B:
",B)
C=np.random.randint(10,size=(4,4))
print("
C:
",C)
D=C.dot(B)
print("
D:
",D)
A:
[[1. 0.]
[0. 1.]]
B:
[[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1]]
C:
[[6 3 1 4]
[2 3 8 2]
[5 4 3 0]
[3 9 6 4]]
D:
[[6 3 1 4]
[2 3 8 2]
[5 4 3 0]
[3 9 6 4]]
对称矩阵
对称矩阵 :元素以主对角线为对称轴对应相等的方阵
对称矩阵的转置是它本身:AT=A
import numpy as np
A = np.random.randint(10,size=(4,4))
print("
A:
",A)
#上矩阵
B = np.triu(A)
print("
B:
",B)
#对称矩阵
C = B + B.T - np.diag(A.diagonal())
print("
C:
",C)
A:
[[3 8 5 4]
[3 2 0 7]
[4 4 7 8]
[2 5 9 8]]
B:
[[3 8 5 4]
[0 2 0 7]
[0 0 7 8]
[0 0 0 8]]
C:
[[3 8 5 4]
[8 2 0 7]
[5 0 7 8]
[4 7 8 8]]
逆矩阵
![]()
消元法
可能一看到逆矩阵,大家就想到代数余子式 ,不过逆天要说的是,代数余子式就和我们程序员面试题一样,有些题目就是又繁琐实际运用又没多大意义的题目一样,很多时候面试官都不看面试题一眼,同样的那些出题老师自己解题一般都不会使用。我这边介绍一下方便简单的方法“消元法”

# coding=utf-8
import numpy as np
A = np.array([[3,2],[1,2]])
print("
A:
",A)
B=np.linalg.inv(A)
print("
B:
",B)
A:
[[3 2]
[1 2]]
B:
[[ 0.5 -0.5 ]
[-0.25 0.75]]
二阶方阵公式

伪逆矩阵


程序比较简单:
np.linalg.det(A)
# coding=utf-8
import numpy as np
#A非方阵
A = np.array([[7, 3, 6],[5, 3, 1]])
print("
A:
",A)
# 有时候还是需要求逆矩阵
# 那就可以求它的伪逆矩阵
B=np.linalg.pinv(A)
print("
B:
",B)
# A*X*A=A
C=A.dot(B).dot(A)
print("
C:
",C)
# X*A*X=X
D=B.dot(A).dot(B)
print("
D:
",D)
# 创建一个矩阵
E = np.mat([[3,2],[1,2]])
print("
E:
",E)
# np.linalg.det(E)不等于0就是可逆
print(np.linalg.det(E)) #4.000000000000001
#E的逆矩阵F
print("
E.I:
",E.I)
F=np.linalg.inv(E)
print("
F:
",F)
G=E*F
print("
G:
",G)
print("
E.T:
",E.T)
A:
[[7 3 6]
[5 3 1]]
B:
[[-0.00632911 0.15189873]
[-0.05696203 0.16708861]
[ 0.20253165 -0.26075949]]
C:
[[7. 3. 6.]
[5. 3. 1.]]
D:
[[-0.00632911 0.15189873]
[-0.05696203 0.16708861]
[ 0.20253165 -0.26075949]]
E:
[[3 2]
[1 2]]
4.000000000000001
E.I:
[[ 0.5 -0.5 ]
[-0.25 0.75]]
F:
[[ 0.5 -0.5 ]
[-0.25 0.75]]
G:
[[1.00000000e+00 2.22044605e-16]
[1.11022302e-16 1.00000000e+00]]
E.T:
[[3 1]
[2 2]]