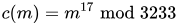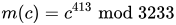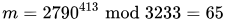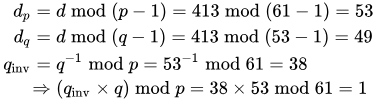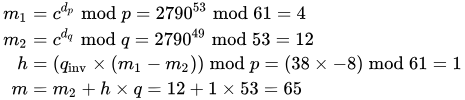https://en.wikipedia.org/wiki/Chinese_remainder_theorem
中国剩余定理
https://en.wikipedia.org/wiki/RSA_(cryptosystem)
The public key is (n = 3233, e = 17). For a padded plaintext message m, the encryption function is
The private key is (n = 3233, d = 413). For an encrypted ciphertext c, the decryption function is
For instance, in order to encrypt m = 65, we calculate
To decrypt c = 2790, we calculate
Both of these calculations can be computed efficiently using the square-and-multiply algorithm for modular exponentiation. In real-life situations the primes selected would be much larger; in our example it would be trivial to factor n, 3233 (obtained from the freely available public key) back to the primes p and q. e, also from the public key, is then inverted to get d, thus acquiring the private key.
Practical implementations use the Chinese remainder theorem to speed up the calculation using modulus of factors (mod pq using mod p and mod q).
The values dp, dq and qinv, which are part of the private key are computed as follows:
Here is how dp, dq and qinv are used for efficient decryption. (Encryption is efficient by choice of a suitable d and e pair)