这是两种简单的素数筛法, 好不容易理解了以后写篇博客加深下记忆
首先, 这两种算法用于解决的问题是 :
求小于n的所有素数 ( 个数 )
比如 这道题
在不了解这两个素数筛算法的同学, 可能会这么写一个isPrime, 然后遍历每一个数, 挨个判断 :
- 从2判断到n-1
bool isPrime(int n) {
for (int i = 2; i < n; i++)
if (n % i == 0)
return false;
return true;
}
- 从2判断到(sqrt{n})
bool isPrime(int n) {
for (int i = 2; i <= sqrt(n); i++)
if (n % i == 0)
return false;
return true;
}
然后再加上个count函数 :
int countPrimes2(int n) {
int cnt = 0;
for(int i = 2; i < n; ++i) {
if(isPrime(i)) cnt++;
}
return cnt;
}
这两种算法, 一个时间复杂度$ O(n^2) $ , 另一个 $ O(n sqrt{n}) $ , 但凡出现这样类型的题, 这么写一般都超时了
下面介绍第一种算法
Eratosthenes 筛法 (厄拉多塞筛法)
核心思想 : 对于每一个素数, 它的倍数必定不是素数
我们通过直接标记, 可以大大减少操作量
比如从2开始遍历, 则4, 6, 8, 10, 12, 14....都不是素数,
然后是3, 则3, 6, 9, 12, 15.....都不是素数
如图更加直观 :
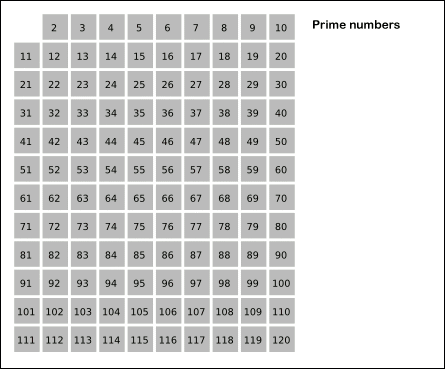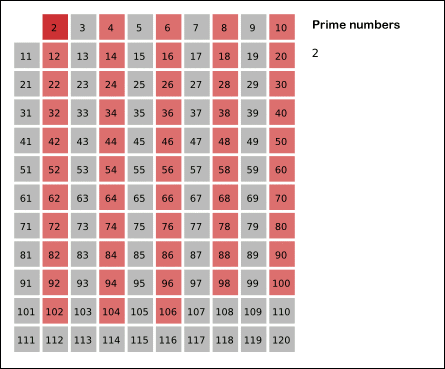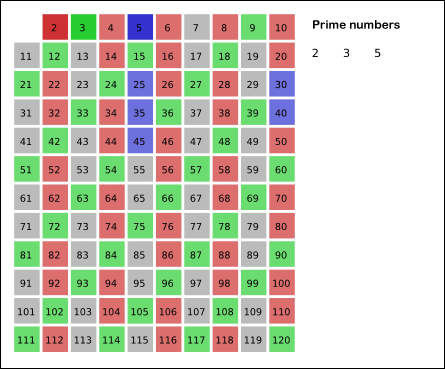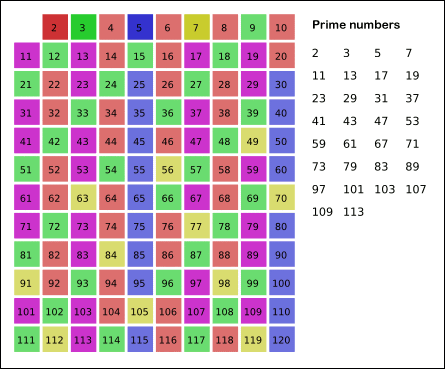
我们可以在判断小于等于数字n的时候增加一个vis数组, 他的大小等于n, 默认vis初始化为全零, 假设2-n都是素数, 接下来每遇到一个素数i, 把2-n中vis[i的倍数] = 1, 在接下来遇到的时候直接跳过就可以.
其时间复杂度为 : $ O(nloglogn) $
代码 :
int countPrimes(int n) {
vector<int> vis(n, 0); // all number : 0 means prime, 1 means not prime
vector<int> prime(n, 0);
int cnt = 0;
for (int i = 2; i < n; ++i) {
if (!vis[i]) { // 如果vis[i]未被标记, 表明i是素数
prime[++cnt] = i;
for (int j = i*2; j < n; j += i) {
vis[j] = 1; // 标记所有i的倍数
}
}
}
return cnt;
}
线性筛作为对Eratosthenes筛的改进, 能更大程度的减少时间复杂度:
O(n)的筛法----线性筛 ( 欧拉筛 )
在讲这个筛法之前, 明确一个概念 :
每一个合数 ( 除了1和它本身以外,还能被其他正整数整除 ), 都可以表示成n个素数的乘积
在Eratosthenes筛中, 我们可以发现, 在排除每一个质数的倍数时, 会有很多重复的操作 :
比如30 = 2x3x5, 那么30将在对2,3,5倍数标记的时候反复被处理3次
我们可以思考, 是否有一种方法, 可以仅仅将一个合数标记一次, 就可以打到筛选的目的呢 ?
可以设立一种规则 :
一个合数只能被他的最小素数因子筛去
比如30, 虽然他有2,3,5三个素因子, 我们只让在对2的倍数作标记时标记30
这样做, 可以保证我们对每一个数都仅仅只操作了一次, 时间复杂度也就变成了喜闻乐见的O(n) !
具体怎样实现 ?
我们在遍历2-n的过程中, 对每一个数i , 从当前已经找到的素数集中从2开始列出prime[j], 当什么时候有:
那么可以说明i含有prime[j]这个素因数, 也就是说, 对于比目前 i x prime[j]更大的数, prime[j]将不再是它的最小素因数, 因此到此这一轮筛可以停止了.
举个例子 :
当 i = 9 时 :
我们可以筛出 :
9 x 2 = 18 ---- 然后进行判断 9%2 != 0, 因此继续筛
9 x 3 = 27 ---- 然后进行判断 9%3 ==0, 因此break
假设我们继续筛 9 x 5, 会发生什么?
由于9 % 3 == 0了, 则可以知道 9含有3这个素因数, 如果继续筛9x5, 可以知道5并不是9x5的最小素因数, 因此不应当在这一轮被筛去.
代码 :
int countPrimes(int n) {
vector<int> vis(n, 0); // all number : 0 means prime, 1 means not prime
vector<int> prime(n, 0);
int cnt = 0;
for (int i = 2; i < n; ++i) {
if (!vis[i])
prime[cnt++] = i;
for(int j = 0; j < cnt && i * prime[j] < n; ++j)
{
vis[i*prime[j]] = 1;
if (i % prime[j] == 0) // if prime[j] is i*prime[j]'s minimum prime
break;
}
}
return cnt;
}
时间比较
写了个cpp计时, 来比较一下这几种算法的时间吧~
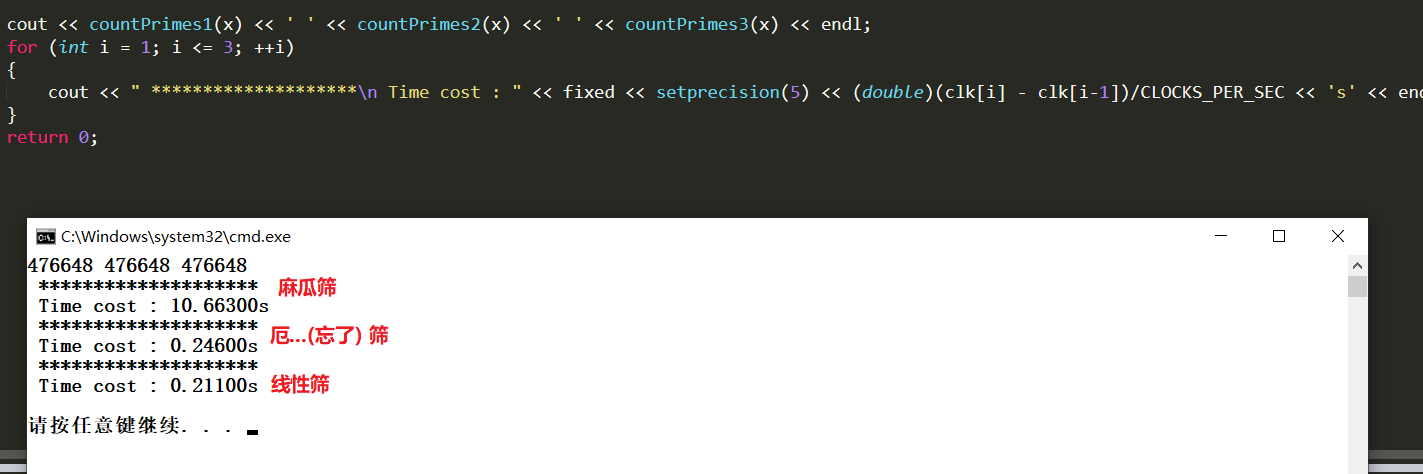
可以看到, Eratosthenes和线性筛的时间稍有区别, 加大数据量会放大这个区别, 但是麻瓜筛(O(n^2)) 在n=7000000的时候已经10s+了, 再加大数据量估计得等到明天了
在写题的这段日子, 每天都在看别人代码的卧槽声中度过
ref :
OI - wiki 筛法 : https://oi-wiki.org/math/sieve/
线性筛法求素数的原理与实现 : https://wenku.baidu.com/view/4881881daaea998fcc220e99.html
leetcode题解 : https://leetcode-cn.com/problems/count-primes/solution/