LCA(最近公共祖先)
LCA,Lowest Common Ancetors,即最近公共祖先。
百度百科定义:“对于有根树T的两个结点u、v,最近公共祖先
表示一个结点x,满足x是u、v的祖先且x的深度尽可能大。”
什么是LCA?
对于一些朋友来说百度百科式的介绍不是很友好,我们在这里形象实际地说明一下什么是LCA。
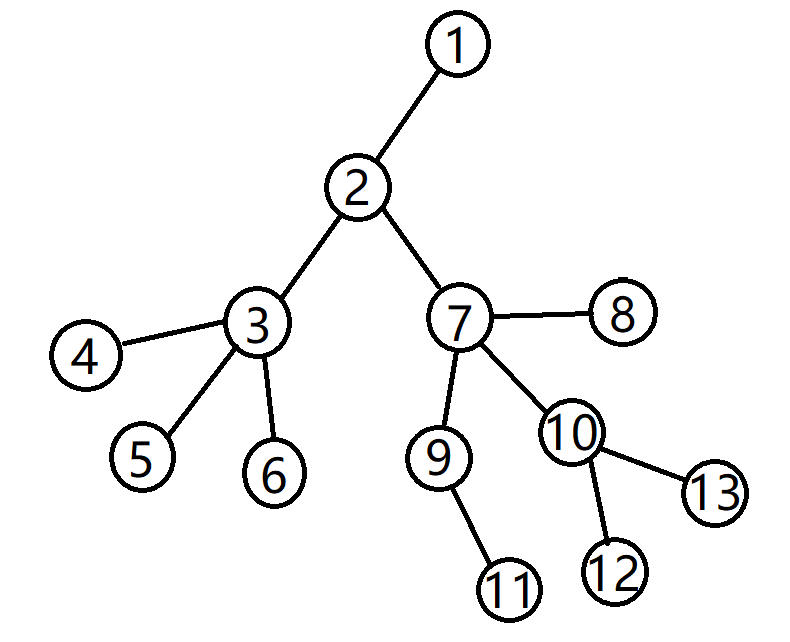
这是一颗树(原谅我手残)
对于u:结点6,v:结点11,根据定义,我们不难找出u,v各自的祖先(父结点)。(顺序由深至浅)
u(结点6):结点3(深度3),结点2(深度2),结点1(深度1)。
v(结点11):结点9(深度4),结点7(深度3),结点2(深度2),结点1(深度1)。
基于LCA定义中“公共”一词,u、v的公共祖先为结点2、结点1。而其中深度最深的结点2即为u(结点6)与v(结点11)的LCA。
而从图上来看,从u/v结点到根结点路径上的所有点都为u/v结点的祖先,而两条路径第一次交汇处的结点即为u与v的LCA。
如何求任意两点间LCA?
主流算法共有4种:
-
倍增
-
Tarjan
-
RMQ(ST表+欧拉序列)
-
树链剖分
其中倍增法较为基础,Tarjan较难理解,RMQ较少见但容易理解,树剖在下并不会(以后再更新绝对不鸽)。
今天我们来研究RMQ(ST表+欧拉序列)求LCA。
RMQ(ST表+欧拉序列)求LCA
前置知识:
-
ST表(DP)
-
DFS
-
链式前向星
梗概:此种方法是通过求出给定树的欧拉序列,通过构造ST表进行给定两点间区间RMQ查询,求出给定两点LCA。
时间复杂度:预处理O(n^2),询问O(1)。
1.欧拉序列
定义:树的欧拉序是对树进行DFS的一种序列。 有两种形式: 1、在每个结点进和出都加进序列。 2、只要到达每一个结点就把他加进序列。
第一种欧拉序列用于树上求和等问题,我们暂且不讲。后一种则是用于求两点LCA等问题。
还是这棵树(原谅我手残):
对这棵树进行DFS,能够得到对于这棵树的欧拉序列。
树上路径 实际访问路径
欧拉序列:1->2->7->8->7->10->13->10->12->10->7->9->11->9->7->2->3->6->3->5->3->4->3->2->1
(值得注意的是由于DFS开始方向不同,欧拉序列整体顺序可能相反)
性质:我们可以发现在欧拉序列中,从树上一点u第一次出现到树上另一点v第一次出现需要遍历u结点所有子树,并回到u结点,进行回溯,遍历u->v树上路径。
而对于这两点的LCA,不难发现LCA一定位于u->v树上路径上且LCA一定是树上路径中最浅结点。由此可以推出,在某颗树的欧拉序列中,给定点u与给定点v的LCA是u在欧拉序列中第一次出现位置与v在欧拉序列中第一次出现位置间形成的区间中深度最浅的点。
(eg.对于上图树中结点6与结点11,其在欧拉序列中形成区间为11->9->7->2->3->6,深度分别为5->4->3->2->3->4,LCA即为最浅点结点2(深度2)。)
P.S. 实际实现时注意两结点第一次出现位置的大小,可能需要交换顺序。
2.ST表
原理我们暂且不讲,不了解的同学可以先将它理解为一种快速查找给定区间最大/最小值(区间RMQ问题)的算法。
在求LCA的过程中,我们所需的ST表与普通ST表略微不同。因为我们在查找最小值时还需要查找此最小值对应的结点编号,以此直接求出LCA。
此问题的解决方法也比较简单,设定一个rec[ ]数组,使其在st表结构数组st[ ]更新时同步更新,查找时比较数组st[ ]得到某一结点深度最浅并返回此结点对应数组rec[ ]中的结点编号。
至此,我们对此算法原理研究结束。
3.代码实现
上代码!
声明部分:
1 #include <iostream> 2 #include <cstdio>//标准输入输出 3 #include <cmath>//用于ST表中求解log 4 using namespace std; 5 int n,m,s,cnt,tot;// s:根结点,cnt:链式前向星,tot:总欧拉序列长度 6 int head[1000005];//链式前向星不解释 7 int depth[1000005];//记录当前结点深度 8 int num[1000005];//记录结点第一次出现位置 9 int rec[2000005][20];//查询数组 10 int st[2000005][20];//ST表结构数组 11 int euler[1000005];//欧拉序列数组 12 //int dp[1000005];求结点深度数组 13 //int wd[1000005];求某一深度树的宽度数组
链式前向星存边:
1 struct edge 2 { 3 int nxt; 4 int to; 5 //int dis;边权值//在本示例中默认边权为1 6 }e[4000005];//建议开4倍数组 7 void add(int x,int y/*,int d*/) 8 { 9 e[++cnt].nxt=head[x]; 10 //e[cnt].dis=d; 11 e[cnt].to=y; 12 head[x]=cnt; 13 }
DFS:
1 void dfs(int x,int dep)//x为当前结点,dep为当前结点深度 2 { 3 4 num[x]=++tot;//记录x结点第一次出现位置 5 depth[tot]=dep;//对应深度 6 euler[tot]=x;//记录序列 7 //dp[x]=max(dp[x],depth[tot]); //求某一结点深度 8 //cout<<"#访问结点:"<<x<<" depth数组:"<<depth[tot]<<endl; 9 for(int i=head[x];i;i=e[i].nxt)//遍历边 10 { 11 int p=e[i].to; 12 if(num[p]==0)//p结点如未出现 13 { 14 dfs(p,dep+1);//遍历 15 euler[++tot]=x;//回溯后记录序列 16 depth[tot]=dep;//记录对应深度 17 } 18 } 19 return ; 20 }
ST表求RMQ:
1 void RMQ(int N)//N:欧拉序列长度 2 { 3 for(int j=1;j<=(int)(log((double)N)/log(2.0));j++) 4 { 5 for(int i=1;i<=N;i++) 6 { 7 if(i+(1<<j)-1<=N) 8 if(st[i][j-1]<st[i+(1<<(j-1))][j-1])//同步更新rec[ ]数组 9 st[i][j]=st[i][j-1],rec[i][j]=rec[i][j-1]; 10 else 11 st[i][j]=st[i+(1<<(j-1))][j-1],rec[i][j]=rec[i+(1<<(j-1))][j-1]; 12 } 13 } 14 } 15 16 int search(int l,int r) 17 { 18 int k=(int)(log((double)(r-l+1))/log(2.0)); 19 if(st[l][k]<st[r-(1<<k)+1][k])//比较后返回rec[ ]数组对应结点编号 20 return rec[l][k]; 21 else 22 return rec[r-(1<<k)+1][k]; 23 }
主函数:
1 int main() 2 { 3 cin>>n>>m>>s; 4 for(int i=1;i<=n-1;i++)//读边 5 { 6 int a,b; 7 scanf("%d %d",&a,&b); 8 add(a,b);//无向图正反存边 9 add(b,a); 10 } 11 dfs(s,1);//开始遍历 12 for(int i=1;i<=tot;i++)//初始化 13 { 14 st[i][0]=depth[i],rec[i][0]=euler[i]; 15 } 16 RMQ(tot);//构建ST表 17 /*//接下来是不必要部分//当初死在了这里 18 int dcnt=0,maxx=0;//dcnt:树的最大深度,maxx:树的最大宽度 19 for(int i=1;i<=n;i++) 20 { 21 wd[dp[i]]++;//统计所有深度为dp[i]的结点求出当前深度的树宽度 22 } 23 for(int i=1;i<=n;i++) 24 { 25 if(wd[i]==0) 26 { 27 break; 28 } 29 dcnt++;//统计最大深度//笨方法 30 } 31 for(int i=1;i<=wcnt+1;i++) 32 { 33 maxx=max(maxx,wd[i]);//求最大宽度 34 } 35 36 */ 37 for(int i=1;i<=m;i++)//查询部分 38 { 39 int l,r,fg=0;//l:结点u,r:结点v,fg:交换标志 40 scanf("%d %d",&l,&r); 41 if(num[l]>num[r])//交换 42 { 43 swap(num[l],num[r]); 44 fg=1;//交换后标记 45 } 46 printf("%d ",search(num[l],num[r]));//查询并输出 47 if(fg==1)//交换回来!!!!!记得交换回来!!!!!//p.s.2019/7/29模拟赛爆0 R.I.P 48 swap(num[l],num[r]); 49 } 50 return 0; 51 }
结语
LCA问题较为常见,应至少掌握一种方法。
拓展:
此种思想也可用于求树(最大)宽度/深度,树上距离,三点LCA等问题。
相关题目
洛谷 P3379 【模板】最近公共祖先(LCA)
洛谷 P3884 [JLOI2009]二叉树问题
洛谷 P4281 [AHOI2008]紧急集合 / 聚会(三点LCA)
//暂时只想到这么多·········
Q.E.D.(大雾)
P.S.
由于是萌新第一次撰写题解,在语言及思路等方面定会有不足之处,请大家多多包涵,也欢迎各位大佬指正。