【NOIP2009】【洛谷P1072】Hankson 的趣味题

问题描述

输入格式

输出格式

样例输入

41 1 96 288

95 1 37 1776

样例输出

提示

数据范围

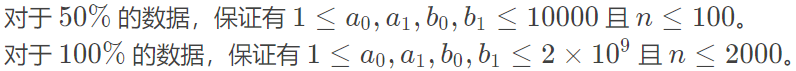
题解

显然直接枚举满足条件的x每次求gcd会超时，我们先尝试两个条件进行转化。

由条件1得gcd(x,a₀)=a₁

不妨设a₁*k₁=x ，a₁*k₂=a₀

那么gcd(k₁,k₂)=1

证明：

假设gcd(k₁,k₂)=1不成立，那么k₁,k₂存在一个大于1的公因数m，则a₁*k₁/m*m=x，a₁*k₂/m*m=a₀

由于m是k₁,k₂的公因数，所以k₁/m,k₂/m为整数

可得gcd(x,a₀)=a₁*m

与前面gcd(x,a₀)=a₁矛盾，所以假设不成立，那么gcd(k₁,k₂)=1是成立的

而k₁=x/a₁,k₂=a₀/a₁，

进一步转化得gcd(x/a₁,a₀/a₁)=1

这样我们得到了x,a₁,a₀的新的关系式

再看条件2，lcm(x,b₀)=b₁=x*b₀/gcd(x,b₀)

得gcd(x,b₀)=x*b₀/b₁

这是一个和条件1相似的式子，类似地，可以转化为gcd(x/(x*b₀/b₁),b₀/( x*b₀/b₁))=1

即gcd(b₁/b₀,b₁/x)=1

结合gcd(x/a₁,a₀/a₁)=1

我们可以先枚举找出b₁的因数x，然后检验x是否是a₁的倍数并且满足以上两个式子，即可找到满足条件的x。这样就减少了求gcd的次数，从而缩短了运行时间。

进一步优化，由埃氏筛法求素数得到启发，x的枚举范围不必从1到b₁，若x是b₁的因数，则b₁/x也是b₁的因数，所以x只需从1枚举到√x

 1 #include <cstdio>
 2 #include <cmath>
 3 int n;
 4 int a0,a1,b0,b1,s;
 5 int gcd(int a,int b)
 6 {
 7     return b?gcd(b,a%b):a;
 8 }
 9 int read()  // 读入优化 
10 {
11     char c=getchar();
12     int x=0;
13     while (c<'0' || c>'9') c=getchar();
14     while (c>='0' && c<='9')
15       x=x*10+c-'0',
16       c=getchar();
17     return x;  
18 }
19 int main()
20 {
21     int i,j;
22     n=read();
23     while (n--)
24     {
25         s=0;
26         a0=read();  a1=read();  b0=read();  b1=read();
27         for (i=1;i*i<=b1;i++)
28         {
29             if (!(b1%i))
30             {
31                 j=b1/i;
32                 if (!(i%a1) && gcd(i/a1,a0/a1)==1 && gcd(b1/b0,b1/i)==1) s++;
33                 if (j!=i && !(j%a1) && gcd(j/a1,a0/a1)==1 && gcd(b1/b0,b1/j)==1) s++;
34             }
35         }
36         printf("%d
",s);
37     }
38     return 0;
39 }