题目link:https://www.luogu.com.cn/problem/UVA1394
Part0:
题意简化:
约瑟夫问题。
给定 $n$ 个编号由 $1$ $ ext{~}$ $n$ 的人,最开始杀掉第 $m$ 个人,接着每数 $k$ 个人就杀掉最后数到的那个,求最后剩下的人的编号。
Part1:
首先容易得出一个 $O(n^2)$ 的用数组循环暴力模拟的算法,但是发现这个算法会枚举到已经死掉的人,因此考虑用链表优化。
Part2:
链表可以 $O(1)$ 进行删除,因此可以 $O(nk)$ 地解决这个问题,但是显然 $n$,$k$ 最大为 $10^4$,$O(nk)$ 过不了此题,所以考虑用递推解决。
这里也给出链表做法的代码:

1 #include <cstdio> 2 3 const int MAXN = 1e4; 4 5 int n, k, m; 6 7 struct Node { 8 int nxt, pre, val, dead; 9 }lst[MAXN + 10]; 10 11 void remove(int id) { 12 13 lst[id].dead = 1; 14 lst[lst[id].nxt].pre = lst[id].pre; 15 lst[lst[id].pre].nxt = lst[id].nxt; 16 17 return; 18 } 19 20 int main() { 21 22 while(233) { 23 24 scanf("%d %d %d", &n, &k, &m); 25 if(!n && !k && !m) return 0; 26 27 for(int i = 1; i <= MAXN; ++i) { 28 lst[i].dead = 0, lst[i].nxt = 0, lst[i].pre = 0, lst[i].val = 0; 29 } 30 lst[1].nxt = 2, lst[1].pre = n, lst[1].val = 1; 31 lst[n].nxt = 1, lst[n].pre = n - 1, lst[n].val = n; 32 for(int i = 2; i < n; ++i) { 33 lst[i].pre = i - 1, lst[i].nxt = i + 1, lst[i].val = i; 34 } 35 36 remove(m); 37 int numKill = 1; 38 int lastKill = m; 39 while(++numKill != n) { 40 for(int i = 1; i <= k; ++i) { 41 lastKill = lst[lastKill].nxt; 42 } 43 remove(lastKill); 44 } 45 46 for(int i = 1; i <= n; ++i) { 47 if(!lst[i].dead) { 48 printf("%d ", i); 49 break; 50 } 51 } 52 53 } 54 55 return 0; 56 }
Part3:
设 $f_i$ 表示 $i$ 个编号为 $ ext{0 ~ i - 1}$ 的人,每次都数到 $k$ 就杀(注意这里是先杀 $k$ $-$ $1$ 不是先杀 $m$ $-$ $1$ 且 为了方便,编号换了一下)。
则递推式为:
$f_i$ $=$ $(f_{i - 1}$ $+$ $k)$ $\%$ $i;$
Part3.1:
举个例子:
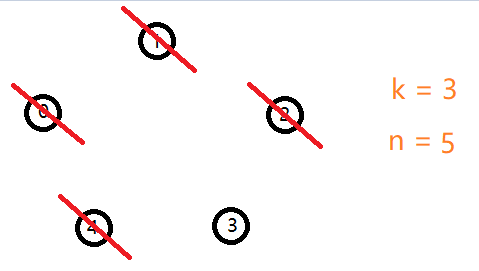
对于一个 $ ext{n = 6,k = 3}$ 的例子。
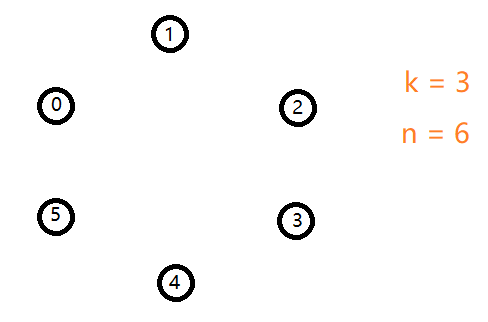
容易发现第一个死掉的人就是 $ ext{2}$ 号。
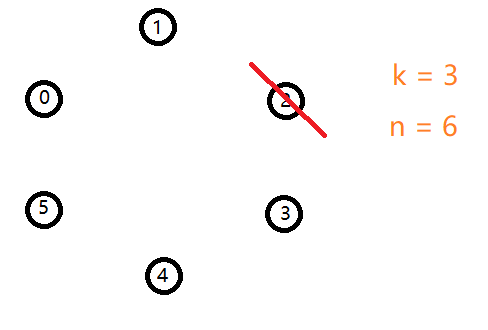
以此类推容易得出最后剩下的人就是 $ ext{0}$ 号。
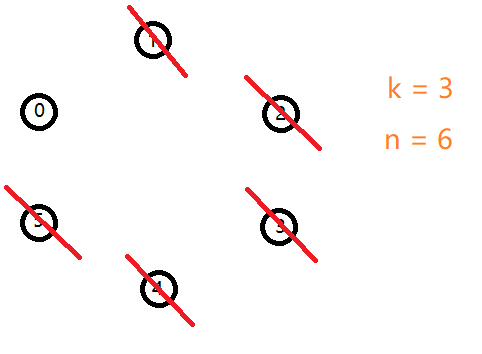
那么对于一个 $ ext{n = 5,k = 3}$ 的例子。
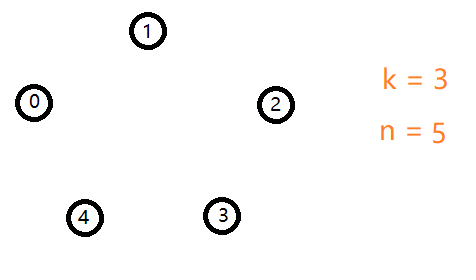
容易得出第一个死的人还是 $ ext{2}$ 号。
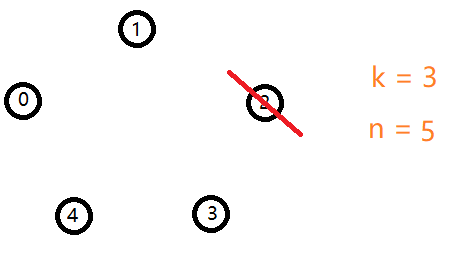
以此类推可以得出最后剩下的人就是 $ ext{3}$ 号。
Part3.2:
对递推式的理解为,在 $ ext{n = 6,k = 3}$ 的图上杀掉第一个人 $ ext{2}$ 号时,从 $ ext{2}$ 号的下一个 $ ext{3}$ 号开始从 $0$ 顺序重新编号。
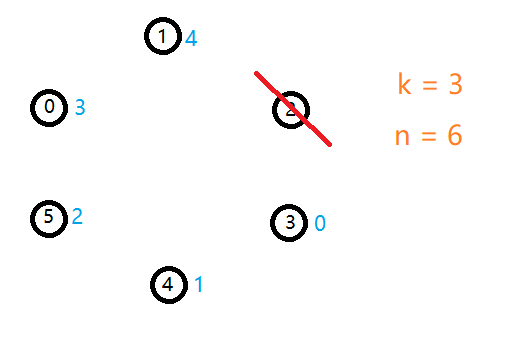
这样一来,容易发现新的编号(蓝色编号),比原来的编号都大了 $k$,而这个新的编号恰好就是 $ ext{n = 5,k = 3}$ 时的图,因此得到 $ ext{n = 5,k = 3}$ 时的解,就可以用那个解 $ ext{+ k}$ 再 $ ext{% n(n = 6)}$ 得到 $ ext{n = 6,k = 3}$ 时的解,如此得到上面的那个递推式也就顺理成章了。
Part4:
但是得到这个递推式后还需要一些修改,因为此题的编号是 $ ext{1 ~ n}$ 而不是 $ ext{0 ~ n - 1}$,杀掉的第一个人是 $m$ 而不是 $k$,具体细节详见代码。
code:
1 #include <cstdio> 2 3 const int MAXN = 1e4; 4 5 int n, k, m, f[MAXN + 10]; 6 7 int main() { 8 9 while(233) { 10 scanf("%d %d %d", &n, &k, &m); 11 if(!n && !k && !m) return 0; 12 f[1] = 0; 13 for(int i = 2; i <= n; ++i) { 14 f[i] = (f[i - 1] + k) % i; 15 } 16 printf("%d ", (((f[n] + (m - k))) % n + n) % n + 1); 17 } 18 19 return 0; 20 }
