线性筛

质数筛

暴力版

从2到根号x扫一遍，如果要求出区间的素数标记数组，复杂度就爆表。

bool isprime(int x){//是不是质数 
    if(x==1) return 0;
    for(int i=2;i*i<=x;i++){
        if(x%i==0)
            return 0;
    } 
    return 1;
}

埃拉托斯特尼筛法（埃氏筛）

　　希腊数学家埃拉托斯特尼提出的筛法，要得到n以内的所有素数，就要把不大于根号n的素数的倍数剔除，留下来的数就是素数了。

　　默认所有数都是素数，从2开始筛，遇到素数就把它的倍数筛掉（素数的倍数不是素数），直到当前素数的平方大于n。

　　在遇到质数想筛它的合数时，不用从2开始，可以从i*i开始，我们设j<i，j如果是素数，在筛j时，那么比他大的i作为倍数肯定筛了，如果j是合数那么在筛j的质因子的时候，i*j就会被筛掉。

　　时间复杂度为O（nlglgn）

bool isprime[maxn];
int prime[maxn];
int init(int n){
    int cnt=0;
    memset(isprime,1,sizeof(isprime));
    for(int i=2;i<=n;i++){
        if(isprime[i]){
            prime[++cnt]=i;
            for(int j=i*i;j<=n;j+=i)
                isprime[j]=0;
        }
    }
    return cnt;
}

欧拉筛

int prime[maxn];
bool isprime[maxn];
int init(int n)
{
    int cnt=0;
    memset(isprime,true,sizeof(isprime));//默认全是质数
    isprime[1]=0;//1不是质数 
    for(int i=2;i<=n;i++)
    {
        if(isprime[i])
            prime[cnt++]=i;
        for(int j=0;j<cnt&&i*prime[j]<=n;j++)
        {
            isprime[i*prime[j]]=0;
            if(i%prime[j]==0)
                break;
        }
    }
    return cnt;//返回小于等于n的素数的个数 
}

　　这个的思想和普通筛一样，但每个合数只会被它的最小质因数筛去。

i从2到n，对于每个i，我们把从2到i的所有质数和i的乘积筛去，为了保证每个合数被它的最小质因数筛去，当i%prime[j]==0时就不往下继续筛了，因为当i是prime[j]的整数倍(记i=m*prime[j])时，i*prime[j+1]=m*prime[j]*prime[j+1],所以i*prime[j+1]的最小质因数是prime[j]，在之后筛除过程中i * prime[j+1] 这个合数一定会被prime[j]筛除，之后的素数同理。

莫比乌斯筛

莫比乌斯函数

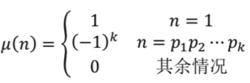
　　现在如果要预处理处理1到n的莫比乌斯函数值，就可以用到上面的素数筛了；

　　对于mu(x)，x是质数的话，mu(x)=-1；

　　如果i%p==0(p是质数),就意味着i有p这个质因子，所以i*p这个数就有p²这个质因子了，于是mu(i*p)=0;

　　如果i%p!=0(p是质数),

欧拉函数筛

欧拉函数筛：

　　欧拉函数：对整数n，欧拉函数是小于n的正整数中与n互质的数的数目。

　　现在分析一下，如果p是质数，那么phi(p)=p-1;

　　　　　　　　　如果n为质数p的k次方，那么phi(n)=p^k-p^k-1,因为一个数不包含质数p的时候才会与n互质，那么包换p的数有1*p，2*p·····，p^k-1*p共p^k-1个，所以phi(n)=n个减p的k-1次方个。(n本身被p^k-1*p减掉了）；

　　　　　　　　　phi(p1p2)=phi(p1)phi(p2)　，很容易证。

　　所以可以推出一个大结论：phi(n)= p1的k次方 * (1−1/p₁) * p2的k次方 * (1−1p₂)

　　　　　　　　　　　　　　　　 =n*(1−1/p₁)* (1−1p₂);

用上素数筛的思想，如果p是x的因数，那么phi(x*p)=phi(x)*p;

　　　　　　　　　如果p不是x的因数，那么phi(x*p)=phi(x)*(p-1);

于是乎，可以线性了：　

const int MAXN=;
bool vis[MAXN];
int prime[MAXN],phi[MAXN];
void init(int n) {
    phi[1] = 1;
    int cnt = 0;
    for (int i = 2; i <= n; i++) {
        if (!vis[i]) {
            prime[cnt++] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; j < cnt && prime[j] <= n / i; j++) {
            vis[prime[j] * i] = true;
            if (i % prime[j])
                phi[i * prime[j]] = phi[i] * (prime[j] - 1);
            else {
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }
        }
    }
}

可以看出，两个函数筛都是基于素数筛的，都是维护了合数的最小质因子。