ML-贝叶斯-原理及实现

1.原理背景

拉普拉斯修正

半朴素贝叶斯

贝叶斯网

scikit-learn实现（GaussianNB，MultinomialNB和BernoulliNB）

https://www.cnblogs.com/pinard/p/6074222.html

1.原理背景

贝叶斯公式：

$P(Y_k|X) = frac{P(X|Y_k)P(Y_k)}{sumlimits_{k}P(X|Y =Y_k)P(Y_k)}$

假如我们的分类模型样本是m个样本，每个样本有n个特征，特征输出有K个类别 ${C_1,C_2,...,C_K}$ ，定义为：

$(x_1^{(1)}, x_2^{(1)}, ...x_n^{(1)}, y_1), (x_1^{(2)}, x_2^{(2)}, ...x_n^{(2)},y_2), ... (x_1^{(m)}, x_2^{(m)}, ...x_n^{(m)}, y_m)$

则朴素贝叶斯的先验分布： $P(Y=C_k)(k=1,2,...K)$ ，易求：Ck出现的次数占比总数m；

条件概率分布： $P(X=x|Y=C_k) = P(X_1=x_1, X_2=x_2,...X_n=x_n|Y=C_k)$ ，难求；

1）用贝叶斯公式得到X和Y的联合分布P(X,Y)：

$P(X,Y=C_k) \ = P(Y=C_k)P(X=x|Y=C_k) \ =P(Y=C_k)P(X_1=x_1, X_2=x_2,...X_n=x_n|Y=C_k)$

2）朴素贝叶斯模型的假设：假设X的n个维度变量之间相互独立，得出：

$P(X_1=x_1, X_2=x_2,...X_n=x_n|Y=C_k) \ = P(X_1=x_1|Y=C_k)P(X_2=x_2|Y=C_k)...P(X_n=x_n|Y=C_k)$

这样就很方便的求出P(X,Y=Ck)了。

对于离散属性：

对于连续属性，基于概率密度，需要假设分布，如高斯分布：

例，根据数据集：

现在要对测试数据x1进行分类：

编号	色泽	根蒂	敲声	纹理	脐部	触感	密度	含糖率	好瓜
x1	青绿	倦缩	浑响	清晰	凹陷	硬滑	0.697	0.460	？（是否）

计算：

1.估计先验概率：

P(好瓜=是)=8/17;P(好瓜=否)=9/17;

2.估计x1中每个属性条件概率

2.1离散类型的计算：

青绿：P青绿|是=P(色泽=青绿|好瓜=是)=3/8，P青绿|否=P(色泽=青绿|好瓜=否)=3/9，

倦缩：P倦缩|是=5/8，P倦缩|否=3/9，

...........

清晰：P清晰|是=P(纹理=清晰|好瓜=是)=7/8，P清晰|否=P(纹理=清晰|好瓜=否)=2/9，

2.2密度类型的计算：

2.3最后预测结果：

Y（好瓜）=是

(8/17)×(3/8)×(5/8)×...×1.959×0.788=0.063

Y（好瓜）=否

(9/17)×(3/9)×(3/9)×...×1.203×0.066=6.8×10^-5;

可见：0.063>6.8×10^-5，所以x1判定为（Y好瓜=是）

拉普拉斯修正

若样本中某个类与某个属性无同时出现，如P(敲声=清脆|好瓜=是)=0/8=0，则有连乘结果为0，其它属性无论怎么好结果都是0，因此将会出现问题，需要进行修正。

从新定义，如：P(好瓜=是)=8+1/17+2=9/19。：

半朴素贝叶斯

因为现实中很难假设的那样，全部相互独立，半朴素贝叶斯假设变量之间存在一些依赖关系。

如这个，假设所有属性都依赖于一个属性y:

假设每个属性依赖类别y以为，还依赖一个超父类属性x1:

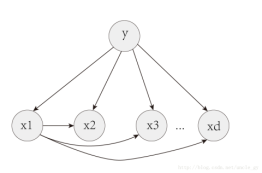
这些情况下计算概率，则要考虑依赖的属性的条件下的概率。

贝叶斯网

把系统中涉及的随机变量，根据是否条件独立绘制在一个有向图中，就形成了贝叶斯网络，也称“信念网”

1）

色泽：直接依赖好瓜&甜度

根蒂：直接依赖甜度...

概率表：P(根蒂=硬挺|甜度=高)=0.1

概率表示为，x3,x4在给定x1时独立，x4,x5在给定x2时独立。：

2）

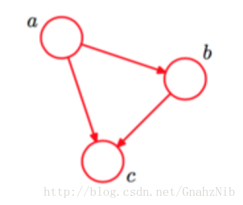
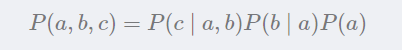
网固定后只需要对参数进行估计，而参数可以直接在训练集上计算得出。因此贝叶斯网的关键是对结构进行搜索。不幸的是，这是个NP难问题。这里不会对这个进行具体编程。

scikit-learn实现（GaussianNB，MultinomialNB和BernoulliNB）

在scikit-learn中，一共有3个朴素贝叶斯的分类算法类。分别是GaussianNB，MultinomialNB和BernoulliNB。其中GaussianNB就是先验为高斯分布的朴素贝叶斯，MultinomialNB就是先验为多项式分布的朴素贝叶斯，而BernoulliNB就是先验为伯努利分布的朴素贝叶斯。

　　　　这三个类适用的分类场景各不相同，一般来说，如果样本特征的分布大部分是连续值，使用GaussianNB会比较好。如果如果样本特征的分大部分是多元离散值，使用MultinomialNB比较合适。而如果样本特征是二元离散值或者很稀疏的多元离散值，应该使用BernoulliNB。

GaussianNB：https://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.GaussianNB.html#sklearn.naive_bayes.GaussianNB

import numpy as np
from sklearn.naive_bayes import MultinomialNB
from sklearn.naive_bayes import BernoulliNB

X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
Y = np.array([1, 1, 1, 2, 2, 2])


'''
GaussianNB类的主要参数仅有一个，即先验概率priors ，对应Y的各个类别的先验概率P(Y=Ck)。
这个值默认不给出，如果不给出此时P(Y=Ck)=mk/m。
其中m为训练集样本总数量，mk为输出为第k类别的训练集样本数。
如果给出的话就以priors 为准。
'''
clf = GaussianNB()
# clf_mu = MultinomialNB()
# clf_be = BernoulliNB()


clf.fit(X, Y)
print('预测类型：', clf.predict([[-0.8, -1]]))
print('预测概率：', clf.predict_proba([[-0.8, -1]]))

#partial_fit功能测试
clf_pf = GaussianNB()
'''
partial_fit方法，这个方法的一般用在如果训练集数据量非常大，一次不能全部载入内存的时候。
这时我们可以把训练集分成若干等分，重复调用partial_fit来一步步的学习训练集，非常方便
'''
# 第三个属性classes：表示可能出现在y向量中的所有类的列表。
# 必须在第一次调用partial_fit时提供，在后续调用中可以省略。
# 这里分2次载入内存
clf_pf.partial_fit(X[:3], Y[:3], np.unique(Y))
print('1批数据载入后，预测类型：', clf_pf.predict([[1, 2.1]]))
print('1批数据载入后，预测概率：', clf_pf.predict_proba([[1, 2.1]]))

clf_pf.partial_fit(X[3:], Y[3:])
print('2批数据载入后，预测类型：', clf_pf.predict([[1, 2.1]]))
print('2批数据载入后，预测概率：', clf_pf.predict_proba([[1, 2.1]]))

'''
预测类型： [1]
预测概率： [[9.99999949e-01 5.05653254e-08]]
1批数据载入后，预测类型： [1]
1批数据载入后，预测概率： [[1. 0.]]
2批数据载入后，预测类型： [2]
2批数据载入后，预测概率： [[2.81846211e-14 1.00000000e+00]]
'''

MultinomialNB：https://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.MultinomialNB.html#sklearn.naive_bayes.MultinomialNB

MultinomialNB假设特征的先验概率为多项式分布,使用MultinomialNB的fit方法或者partial_fit方法拟合数据后，我们可以进行预测。此时预测有三种方法，包括predict，predict_log_proba和predict_proba。由于方法和GaussianNB完全一样.

BernoulliNB：https://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.BernoulliNB.html#sklearn.naive_bayes.BernoulliNB

BernoulliNB假设特征的先验概率为二元伯努利分布，使用也是一致的