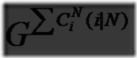就是一道赤裸裸的数论题拉。
在cxms众牛的激烈讨论下,最终没有做出本题。
其实,我们只是差了一步。
从头来。
显然P是一个质数。
如果我们已知![]() ,则我们可以利用快速幂在
,则我们可以利用快速幂在![]() 时间内求出答案。现在问题聚焦到求解
时间内求出答案。现在问题聚焦到求解![]() 上。由于N的所有约数可以利用枚举约数方法在
上。由于N的所有约数可以利用枚举约数方法在![]() 时间内求得,所以问题的关键即是求解
时间内求得,所以问题的关键即是求解![]() 。(然后到这里我们都无力了。)Lucas定理和欧拉-费马定理能在
。(然后到这里我们都无力了。)Lucas定理和欧拉-费马定理能在![]() 时间内解决这个关键问题。但是,必须满足模数是质数!
时间内解决这个关键问题。但是,必须满足模数是质数!
怎么办?怎么办?怎么办?然后很自然的就想到了质因数分解按每个质因数求解答案后利用线性模方程组的扩展GCD或中国剩余定理方法来完美解决。
粗估总复杂度为:
总结一下出现过的所有数论知识:
枚举约数方法:枚举i从![]() ,若
,若![]() ,则i和N/i均为N的两个约数。注意
,则i和N/i均为N的两个约数。注意![]() 的情况。
的情况。
质因数分解:每一个大于1的整数都能分解成质因数乘积的形式,并且如果把质因数按照由小到大的顺序排列在一起,相同的因数的积写成幂的形式,那么这种分解方法是唯一的。
线性模方程组和扩展GCD和中国剩余定理:详见本博客第一篇日志。
发现我的数论知识面貌似这道题里面已经基本全部包括了。
/*
Problem:
[SDOI2010]古代猪文
Algorithm:
Note:
*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<set>
#include<vector>
#include<map>
#include<string>
#include<iomanip>
#include<iostream>
#include<cmath>
using namespace std;
#define rep(i,x,y) for(i=x;i<=y;i++)
#define _rep(i,x,y) for(i=x;i>=y;i--)
#define CL(S,x) memset(S,x,sizeof(S))
#define mp make_pair
//#define x first
//#define y second
//#define MAX(x,y) ((x)>(y)?(x):(y))
//#define MIN(x,y) ((x)<(y)?(x):(y))
//#define sqr(x) ((x)*(x))
typedef long long int64;
typedef long double real;
int64 N,G;
int64 c[36000];
int64 ans[5][2];
int i;
int64 gcd(int64 a,int64 b,int64 &x,int64 &y)
{
if(b==0){x=1;y=0;return a;}
int64 ans=gcd(b,a%b,y,x);y-=a/b*x;
return ans;
}
int64 pow(int64 x,int64 y,int64 mod)
{
if(y==0)return 1;
int64 ans=pow(x,y/2,mod);
ans=ans*ans%mod;
if(y&1)ans=ans*x%mod;
return ans;
}
int64 C(int64 a,int64 b,int64 mod)
{
if(a<b)return 0;
return c[a]*pow(c[b]*c[a-b]%mod,mod-2,mod)%mod;
}
int64 solve(int64 a,int64 b,int64 mod)
{
if(b==0)return 1%mod;
return C(a%mod,b%mod,mod)*solve(a/mod,b/mod,mod)%mod;
}
int64 work(int64 mod)
{
int64 i;
c[0]=1;rep(i,1,mod-1)c[i]=c[i-1]*i%mod;
int64 maxm=int64(sqrt(N));
int64 ans=0;
rep(i,1,maxm)
if(N%i==0)
{
ans=(ans+solve(N,i,mod))%mod;
if(i*i!=N)ans=(ans+solve(N,N/i,mod))%mod;
}
return ans;
}
int main()
{
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
cin>>N>>G;
ans[1][0]=2;ans[1][1]=work(2);
ans[2][0]=3;ans[2][1]=work(3);
ans[3][0]=4679;ans[3][1]=work(4679);
ans[4][0]=35617;ans[4][1]=work(35617);
rep(i,2,4)
{
int64 x,y;
int64 r=gcd(ans[i-1][0],-ans[i][0],x,y);
ans[i][1]=x*((ans[i][1]-ans[i-1][1])/r)*ans[i-1][0]+ans[i-1][1];
ans[i][0]=ans[i-1][0]*ans[i][0]/abs(r);
ans[i][1]=(ans[i][1]%ans[i][0]+ans[i][0])%ans[i][0];
}
if(ans[4][1]==0)ans[4][1]=ans[4][0];
cout<<pow(G,ans[4][1],int64(999911659))<<endl;
scanf("\n");
return 0;
}