概论
分层图,即拆点,是图论问题中一种常见的建图技巧,应用较为广泛。深入理解并掌握这种技巧,对设计算法解决一些图论问题会颇有助益。
类比动态规划中的状态机模型,当单纯的一个点无法表示清楚其上信息时,我们可以考虑拆点,将一个状态拆成多个状态,这样就可以把信息理清楚了。李煜东在《算法竞赛进阶指南》中指出,动态规划对状态空间的遍历构成一张有向无环图,遍历顺序就是该有向无环图的一个拓扑序。拆点分层之后如何建边,以及原问题的答案对应分层图中的哪个点,我们都可以通过动态规划的思想来考虑,然后将其还原回图中。
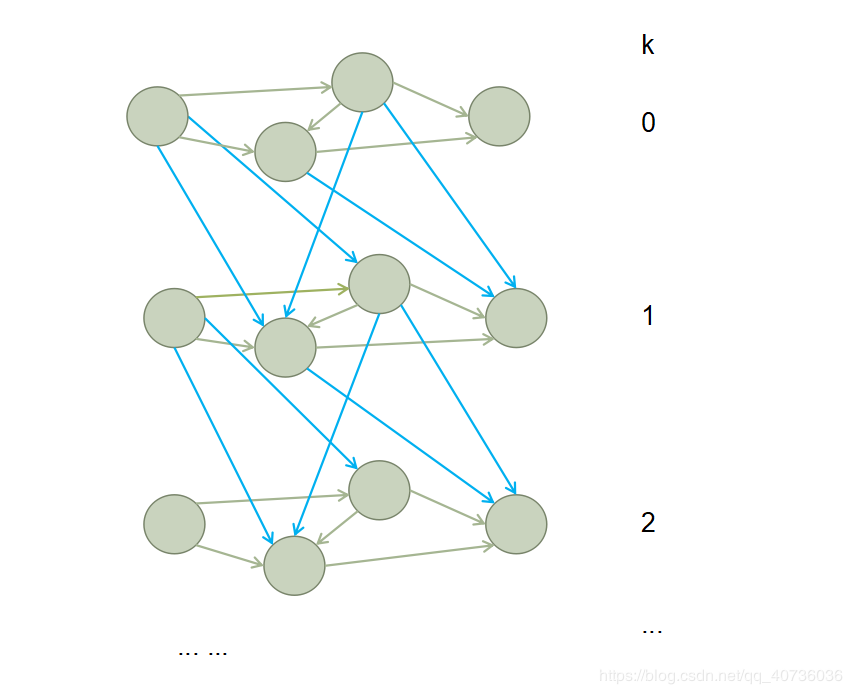
分层图的一般模型为:在原图上,进行k次特殊操作,然后求解。我们一般便会将原图复制成k+1张完全一样的图,每张图分别表示进行了0次、1次、2次、……、k次特殊操作,然后在图之间(即每一层之间)根据某些关系连边。
最后的图大概长这个样子:
例题
[POJ3662]通信线路
题意简述
在无向图上求出一条从1到N的路径,可指定路径上K条边权值为0,然后最小化路径上的最大边权。
算法概述
这题是分层图最短路的一道典型例题。
考虑dp[p,k]表示从1号点到p号点,当前已经指定了k条边权值为0时,路径上权值最大的边权是多少。考虑其任一出边(p,v,w),则dp[p,k]能够更新的状态有dp[v,k]=max(dp[p,k],w)①,dp[v,k+1]=dp[p,k]②。
根据上述动态规划的思想建立分层图,将dp的状态表示记为点,如dp[p,k]则记为p+k*n,这样可以防止点号的重复。对于①式,dp[v,k]与dp[p,k]同在第k+1层,之间连原边即可,即从p+k*n向v+k*n连一条权值为w的边。对于②式,则由p+k*n向v+(k+1)*n连一条权值为0的边。
注意是无向图,故边连双向。
最后答案的答案,我们可以先看dp状态,根据我们dp的状态表示,最后的答案应是dp[n,0],dp[n,1],dp[n,2],…,dp[n,k]中的最小值,所以对应到图上,即为n,2*n,3*n,…,(k+1)*n上的最短距离。
有一个比较偷懒的技巧,可以在跑最短路之前,从n向2*n,2*n向3*n,…,k*n向(k+1)*n连一条长度为0的单向边,这样答案就只需要看(k+1)*n上的值即可。
用Dijkstra算法的时间复杂度是O(km*logkn)。
当然这题还有二分答案转化为01最短路问题的解法,我们在此不予赘述。这个解法有很大局限性,我们可以看到,下一道例题,仅仅是最后询问不同,却无法用这种解法解决,但分层图的做法仍能很好地解决。
参考代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N=1e3+10,M=4e7+10,MAXK=1e3+10;
struct Edge{
int to,next,w;
}edge[M]; int idx;
int h[N*MAXK];
int dis[N*MAXK],vis[N*MAXK];
int n,m,K;
void add_edge(int u,int v,int w){edge[++idx]={v,h[u],w};h[u]=idx;}
void dijkstra()
{
memset(vis,0,sizeof vis);
memset(dis,0x3f,sizeof dis);
priority_queue<pair<int,int> > q;
dis[1]=0;
q.push(make_pair(0,1));
while(!q.empty())
{
int k=q.top().second;
q.pop();
if(vis[k])continue;
vis[k]=1;
for(int i=h[k];~i;i=edge[i].next)
{
int to=edge[i].to,w=edge[i].w;
if(dis[to]>max(dis[k],w))
{
dis[to]=max(dis[k],w);
q.push(make_pair(-dis[to],to));
}
}
}
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d%d%d",&n,&m,&K);
while(m--)
{
int u,v,w;scanf("%d%d%d",&u,&v,&w);
for(int i=0;i<=K;i++)
{
add_edge(u+i*n,v+i*n,w);
add_edge(v+i*n,u+i*n,w);
}
for(int i=0;i<K;i++)
{
add_edge(u+i*n,v+(i+1)*n,0);
add_edge(v+i*n,u+(i+1)*n,0);
}
}
dijkstra();
if(dis[(K+1)*n]==0x3f3f3f3f)printf("-1
");
else printf("%d
",dis[(K+1)*n]);
return 0;
}
[JLOI2011]飞行路线
题意简述
给定一张无向图,可以指定图中k条边权值为0,求给定两点s,t之间的最短路径。
算法概述
裸的分层图,分析见上题,算法中唯一不同之处即为求路径上最大边权改为求路径上边权总和。
参考代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N=1e4+10,M=5e4+10,MAXK=11;
struct Edge{
int to,next,w;
}edge[M*MAXK*4]; int idx;
int h[N*MAXK];
int dis[N*MAXK],vis[N*MAXK];
int n,m,K,s,t;
void add_edge(int u,int v,int w){edge[++idx]={v,h[u],w};h[u]=idx;}
void dijkstra(int s)
{
memset(vis,0,sizeof vis);
memset(dis,0x3f,sizeof dis);
priority_queue<pair<int,int> > q;
dis[s]=0;
q.push(make_pair(0,s));
while(!q.empty())
{
int k=q.top().second;
q.pop();
if(vis[k])continue;
vis[k]=1;
for(int i=h[k];~i;i=edge[i].next)
{
int to=edge[i].to,w=edge[i].w;
if(dis[to]>dis[k]+w)
{
dis[to]=dis[k]+w;
q.push(make_pair(-dis[to],to));
}
}
}
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d%d%d",&n,&m,&K);
scanf("%d%d",&s,&t);
while(m--)
{
int u,v,w;scanf("%d%d%d",&u,&v,&w);
for(int i=0;i<=K;i++)
{
add_edge(u+i*n,v+i*n,w);
add_edge(v+i*n,u+i*n,w);
}
for(int i=0;i<K;i++)
{
add_edge(u+i*n,v+(i+1)*n,0);
add_edge(v+i*n,u+(i+1)*n,0);
}
}
for(int i=0;i<K;i++)add_edge(t+i*n,t+(i+1)*n,0);
dijkstra(s);
printf("%d
",dis[t+K*n]);
}
[CH6101]最优贸易
题意简述
给定一张有向图,无边权,每个点有一个点权w,求从1到n的路径上,w[q]-w[p]的最大值。其中p和q为路径上的点,且必须先经过p再经过q。
算法概述
一个简单的做法是跑正着求一遍以1为源点的最短路,反着求一遍以n为源点的最长路,然后枚举每个点,两个dist作差取max即可(具体可看下面附的代码)。
但是这种做法也有局限,当图中有边权存在时,这种做法就不太好做了。
所以这里介绍一种通用的做法——分层图最短路。
还是先看以dp的思想来分析,设dp[p,s]为从1到p这个点,当前p的状态为s的最长路,其中s=0,1,2。0表示当前还未进行交易,1表示当前已买入但未卖出,2表示当前已完成一次交易(即已买入且卖出一次)。
考虑状态转移,首先dp[p,1]=dp[p,0]-w[p],dp[p,2]=dp[p,1]+w[p],其次对于p的每一条出边(p,v),dp[v,s]=dp[p,s]。
故我们可建立三层完全一样的图,然后考虑层间的建边,对于每个点,只需从p向p+n连一条长度为-w[p]的边,从p+n向p+2*n连一条长度为w[p]的边即可。
最后答案即为dp[n,2],也就是3*n这个点上的信息。
参考代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N=3e5+10,M=1e6+10;
struct Edge{
int to,next,w;
}edge[3*M+N];int idx;
int h[N];
void add_edge(int u,int v,int w){edge[++idx]={v,h[u],w};h[u]=idx;}
int dis[N],vis[N];
int price[N];
int n,m;
void spfa()
{
memset(vis,0,sizeof vis);
memset(dis,-0x3f,sizeof dis);
queue<int> q;
dis[1]=0,vis[1]=1;
q.push(1);
while(!q.empty())
{
int p=q.front();
q.pop();
vis[p]=0;
for(int i=h[p];~i;i=edge[i].next)
{
int to=edge[i].to,w=edge[i].w;
if(dis[to]<dis[p]+w)
{
dis[to]=dis[p]+w;
if(!vis[to])
{
q.push(to);
vis[to]=1;
}
}
}
}
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&price[i]);
while(m--)
{
int a,b,c;scanf("%d%d%d",&a,&b,&c);
for(int i=0;i<3;i++)
{
add_edge(a+i*n,b+i*n,0);
if(c==2)add_edge(b+i*n,a+i*n,0);
}
}
for(int i=1;i<=n;i++)
{
add_edge(i,i+n,-price[i]);
add_edge(i+n,i+n+n,price[i]);
}
spfa();
printf("%d
",dis[3*n]);
return 0;
}
附:
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int N=1e5+10,M=2e6+10;
struct Edge{
int to,ne;
}edge1[M<<1],edge2[M<<1]; int idx1,idx2;
int h1[N],h2[N];
int n,m;
int d[N],vis[N],f[N];
int price[N];
void add_edge(Edge edge[],int h[],int &idx,int u,int v)
{
edge[++idx].to=v;
edge[idx].ne=h[u];
h[u]=idx;
}
void SPFA(int dis[],int s,int lab,Edge edge[],int h[])
{
if(!lab)memset(dis,0x3f,sizeof d);
else memset(dis,-0x3f,sizeof f);
dis[s]=price[s];
queue<int> q;
q.push(s);
vis[s]=1;
while(!q.empty())
{
int k=q.front();
q.pop();
vis[k]=0;
for(int i=h[k];~i;i=edge[i].ne)
{
int to=edge[i].to;
if(!lab)
{
if(dis[to]>min(dis[k],price[to]))
{
dis[to]=min(dis[k],price[to]);
if(!vis[to]){q.push(to);vis[to]=1;}
}
}
else
{
if(dis[to]<max(dis[k],price[to]))
{
dis[to]=max(dis[k],price[to]);
if(!vis[to]){q.push(to);vis[to]=1;}
}
}
}
}
}
int main()
{
memset(h1,-1,sizeof h1);
memset(h2,-1,sizeof h2);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&price[i]);
for(int i=1;i<=m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add_edge(edge1,h1,idx1,a,b);
add_edge(edge2,h2,idx2,b,a);
if(c==2)
{
add_edge(edge1,h1,idx1,b,a);
add_edge(edge2,h2,idx2,a,b);
}
}
SPFA(d,1,0,edge1,h1);
SPFA(f,n,1,edge2,h2);
int res=0;
for(int i=1;i<=n;i++)
res=max(res,f[i]-d[i]);
printf("%d
",res);
return 0;
}