一、拟合问题
1、什么叫做拟合?
(x,y)直接的关系可以用一条线(直线或者曲线)表达,我们的目标就是找到这一条线,找到线的关键就是求取参数
2、公式
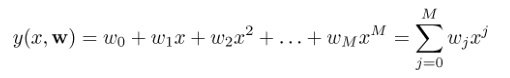
单特征,ω代表参数,y(x,w)是估计值,t是实际值
3、如何求取参数ω?三种方法:
(1)确定性方法:将参数w和t看成确定性的量,只是值不知道而已
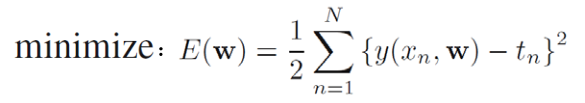
E(w):均方误差; y(xn,w):第二个样本的估计值; tn:第二个样本的实际值; 1/2:方便之后的计算
采用确定性方法,就是求出使得E(w)最小的那个w
对于y(xn,w):
M=0:一条平行于X轴的直线()
M=1:一次方程,一条直线(需要一个样本就可以求取)
M=2:二次方程,一条曲线
.......
如果训练样本数量过小,可以拟合出一条满足所有样本的线,此时容易产生过拟合现象,如何解决?
(1.1)增加训练样本数
(1.2)正则化:增加惩罚因子
(2)最大似然估计:将参数w看成确定性的量,只是值不知道而已;将产生的值看成一种概率表达
(3)贝叶斯估计:将参数w看成随机量,存在概率分布;将产生的值看成一种概率表达
二、线性回归
1、什么是线性回归?
(1)线性:直线
(2)线性回归:根据已有的数据集拟合出一条直线
(3)用途:回归或者分类,如果y是连续的值,则为回归;如果y是离散的几个值,则为分类;本文只针对分类
(4)线性公式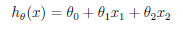 ,设置x0=1,则有
,设置x0=1,则有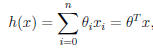 ,n为特征个数
,n为特征个数
(5)如果利用线性回归进行回归或者分类,只需要估算出θ的值
2、如何估算θ?
代价函数:m-学习样本个数
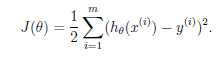
目标:求得使J(θ)最小的θ,如何求?
(1)梯度下降
(1.1)单样本的梯度下降:
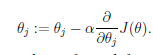
θj:第j个参数,需要设定一个初始值,初始值的设定会影响到梯度下降的结果
α:学习速度,决定了下降的步长。如果设置过小,会导致收敛速度过慢;如果太大,可能会越过最小值

---->最小均方误差: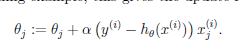
对于多样本,有两种方法可以处理:
(2.2)批梯度下降
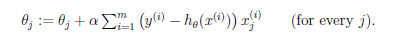
批:每次迭代都用到所有样本
优点:总是会收敛到全局最小值
缺点:如果训练集合太大,则效率太低
检测收敛:设定阈值ε,如果两次迭代改变小于阈值,则认为收敛
(2.3)随机梯度下降(增量梯度下降)
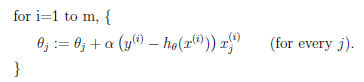
随机:每次值选取一个样本更新θj,循环m轮
有点:效率高,收敛速度快,大数据集更倾向于增量梯度下降
缺点:在全局最小值附近徘徊,不会精确收敛到全局最小值
(2)最小二乘法
直接求J(θ)的导数,置为0,求θ
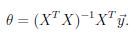
3、参数学习算法与非参数学习算法
参数学习算法:拟合参数θ数量固定---容易发生过拟合和欠拟合
非参数学习算法:拟合参数θ数量不固定,参数数量会随着训练集合的大小线性增长,需要保存整个训练集--不能完全避免过拟合与欠拟合
4、局部加强线性回归----一种非参数学习算法
(1)什么是局部加强?
原始的线性回归,关注全局样本,用所有的训练样本找到拟合参数,问题是一条直线往往并不能很好的拟合,曲线可能会更好的反应样本情况,局部加强就是针对这种问题
局部加强更关注邻近区域,为邻近区域赋予比较大的权值,为偏远区域赋予较小的权值
代价函数:
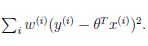
(2)如何计算权值?
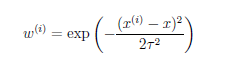
有很多种计算方式,这是其中之一---指数衰减函数
τ:波长参数,控制权值随距离下降的速率,越小下降越快
三、logistic回归
1、为什么要用logistic回归?
普通的线性回归,计算的h(θ)的值范围非常大,利用logistic回归,可以将h(θ)的范围缩小到(0,1)
2、logistic函数(sigmoid函数):
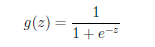
z=0时,值为0.5; z>>0时,值为1; z<<0时,值为0
3、logistic回归函数
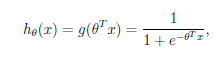
4、求拟合参数
假设: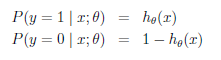 ----->
----->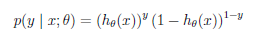
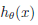 >0.5,则为正例,否则为反例
>0.5,则为正例,否则为反例
logistic回归就是要学习到θ,使得正例(y=1)的特征远大于0,即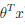 >>0, 负例(y=0)的特征远小于0,即
>>0, 负例(y=0)的特征远小于0,即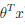 <<0
<<0
通过极大似然估计可得:
 -->
-->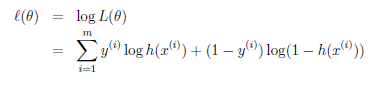 --->
--->
求取使得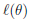 最大的θ:
最大的θ:
(1)梯度上升
![]() ---->
---->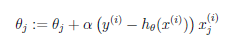
(2)牛顿方法?
(2.1)为了得到最大的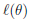 ,第一个办法是按照上面的梯度上升,直到两次的变化小于设定的某个阈值;第二个办法是对其直接求导,并置导数为0
,第一个办法是按照上面的梯度上升,直到两次的变化小于设定的某个阈值;第二个办法是对其直接求导,并置导数为0
(2.2)牛顿方法是什么?
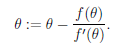 此为牛顿方法的一次迭代,通过不断的迭代最后找到使得f(θ)=0
此为牛顿方法的一次迭代,通过不断的迭代最后找到使得f(θ)=0
换句话说,牛顿方法的目标是f(θ)=0,我们的目标是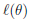 的导数=0,那我们只需要设置:
的导数=0,那我们只需要设置:
![]() --->
--->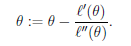
(2.3)优点:收敛速度快,号称二次收敛(0.01->0.0001->0.00000001)
缺点:如果特征数目太多,效率低,所以比较适合特征少的情况(不过,通常情况情况下,特征数目都不多)
四、总结与疑问
1、这些计算方法直接的关系:极大似然估计、贝叶斯估计、梯度、最小二乘、牛顿(待)
2、线性回归为什么不适合用来进行分类?
3、极大似然与最小二乘?
....乱乱乱