单变量的线性回归非常容易理解,就是生成一元一次方程:
| 地推人员数量 | 卖出会员数量 |
| 1 | 14 |
| 2 | 24 |
| 2 | 18 |
| 1 | 17 |
| 3 | 27 |
![]()
应用层面可以直接拿公式套,甚至公式也不用记,开源库都封装好了方法,传入样本数据即可得方程式。
本着不光知其然还要知其所以然的态度,查阅了一些资料,总结成自己最易理解的语言阐述下求解过程。
求解过程:
令f(x,y)=∑(Yi-(a*Xi+b))^2,将样本点代入,并将a、b转为常见的x、y变量。得出:
f(x,y)=(1x+y-14)^2+ (2x+y-24)^2+ (2x+y-18)^2 + (1x+y-17)^2+ (3x+y-27)^2
f(x,y)是一个二元二次分布式,看一下它的三维图像:
上图x、y坐标显示很清晰,但是z坐标不立体,换个角度看:
从上图可以看出,这个图像是有谷底的,谷底就是f(x,y)的最小值。
在谷底处,不管x坐标,还是y坐标,其斜率都是0,也就是x和y的导数都是0。
所以,求f(x,y)的最小值就是求x导数=0和y导数=0。这个结论是重点、重点、重点!
为什么强调它,是因为查阅的N多文章都直接抛出:求f(x,y)的最小值就是求x和y的导数。这句话有2个问题:
一、怎么得出这个结论的?
二、x和y的导数是个函数,f(x,y)的最小值应该是个固定值,怎么能划等号?
后来看到一篇严谨的文章说:求f(x,y)的最小值是求x和y的导数等于0,并不能仅仅说求x和y的导数。
问题二解决了,可是问题一依然困惑。
一元二次方程求极值=求一元变量导数等于0,这个容易理解是因为抛物线的图像深入我心。
那不如类比一下,看看二元二次方程的图像吧。这才有了上面两个三维图像的来源。用python Axes3D画的。
看这个图像就很容易理解为什么要求导、为什么求两个变量的、为什么导数应该等于0了!
现在来重温下求导的知识点:
- 基本求导公式
比如 y=x^2,求y的导数,按照上述步骤:
Δy=(x+Δx)^2-x^2=2xΔx+Δx^2 ;Δy/Δx=2x+Δx ;Δx趋于0,所以y的导数=2x。
- 导数的四则运算法则
(u+v)'=u'+v'
(u-v)'=u'-v'
(uv)'=u'v+uv'
(u/v)'=(u'v-uv')/v^2
- 复合函数维度下降法求导
f[g(x)]中,设g(x)=u,则f[g(x)]=f(u),f'[g(x)]=f'(u)*g'(x)
比如y=(3x-2)^2,令y=u^2,u=3x-2. y'(x)=y'(u)*u'(x)=2*(3x-2)*3=18x-12.
现在可以对 f(x,y)=(1x+y-14)^2+ (2x+y-24)^2+ (2x+y-18)^2 + (1x+y-17)^2+ (3x+y-27)^2 求导了 :
x导数=2*(x+y-14)*1+2*(2x+y-24)*2+2*(2x+y-18)*2+2*(x+y-17)*1+2*(3x+y-27)*3
y导数=2*(x+y-14)*1+2*(2x+y-24)*1+2*(2x+y-18)*1+2*(1x+y-17)*1+2*(3x+y-27)*1
目的是求得x导数=0、y导数=0时的x、y值。即:
(x+y-14)+(2x+y-24)*2+(2x+y-18)*2+(x+y-17)+(3x+y-27)*3=0
(x+y-14)+(2x+y-24)+(2x+y-18)+(x+y-17)+(3x+y-27)=0
即:
19x+9y=196
9x+5y=100
这是一个二元一次方程,很容易求得:x=5.7142,y=9.7142.
下面证明简化版的求解公式是怎么来的:
分别对a和b求一阶偏导,求导后让其等于0,然后联立方程组解得参数a和b。



套用这个公式,依然求得:a=5.7142,b=9.7142.
看下二元方程图像求极值的代码,比较结果是否和求导/套用公式的一致:
import numpy as np
if __name__ == '__main__':
x = np.arange(0, 20, 0.1)
y = np.arange(0, 20, 0.1)
x, y = np.meshgrid(x, y)
z = (1*x+y-14)**2+ (2*x+y-24)**2+ (2*x+y-18)**2 + (1*x+y-17)**2+ (3*x+y-27)**2
q=[]
for i in range(0,200,1):
q.append(z[i])
z=z.flatten()
w= min(z)
print ("损失函数的最小值是: "+str(w))
for i in range(200):
for j in range(200):
if q[i][j]==w:
break
else:
continue
break
print ("a、b参数的值分别是: "+str(x[i][j])+" , "+str(y[i][j]))
输出:
损失函数的最小值是: 22.58
a、b参数的值分别是:5.7 , 9.7
这个结果精度不如前面两个。原因在于x、y坐标移动步长0.1还可以更小。
如果步长太小又会导致性能变差。顺着这个思路,就不难理解梯度下降法了。
实际项目都是用计算机的梯度下降法来求极值,所以求导部分理解即可,不用强记。
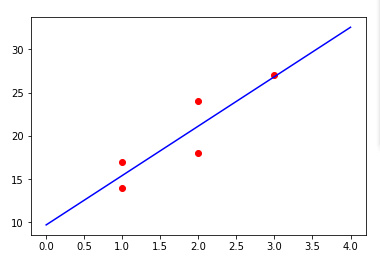
最后看下最优直线长什么样子吧: