Introduction
The goal of the 3D spherical kernel is to offer to the user a large set of functionalities on spheres, circles and circular arcs, in the 3D space or restricted on a given sphere. These functionalities require computing on algebraic numbers, which motivates the creation of a new kernel concept extending the CGAL Kernel concept, that is restricted to objects and functionality in a FieldNumberType.
All the choices (interface, robustness, representation, and so on) made here are consistent with the choices made in the CGAL kernel, for which we refer the user to the 2D and 3D Linear Kernel).
3D spherical kernel 的目标是给用户提供3D空间或严格地在给定球上的一套大量的面向球体、圆和圆弧的功能函数。这引起功能函数要求代数数的计算,激发了由概念CGAL Kernel扩展而创建一个新的内核,这个内核严格地使用基于FieldNumberType的对象和函数。
Spherical Kernel Objects
New main geometric objects are introduced by Spherical_kernel_3: circular arcs ((model of SphericalKernel::CircularArc_3), points of circular arcs (model of SphericalKernel::CircularArcPoint_3), and line segments (model of SphericalKernel::LineArc_3) whose endpoints are points of this new type.
SphericalKernel::CircularArcPoint_3 is used in particular for endpoints of arcs and intersection points between spheres, circles or arcs. The coordinates of these points are algebraic numbers of degree two. Therefore, general predicates offered by the Kernel on Point_3, which have coordinates in a FieldNumberType, would require heavy algebraic computations in algebraic extensions of higher degrees and thus are not provided on them, which explains the need for a new point type.
A consistent set of predicates and constructions is offered on these new types.
新的主几何对象由Spherical_kernel_3引入:圆弧((SphericalKernel::CircularArc_3概念的模型),圆弧上的点(SphericalKernel::CircularArcPoint_3概念的模型,和线段),线段(SphericalKernel::LineArc_3的模型)它的端点是是圆弧上的点)。
是特别用于圆弧的端点和球体、圆或弧的交集。这些点的坐标是2级代数数(algebraic numbers of degree two)。所以,本Kernel提供的面向 Point_3的通用判定(具有FieldNumberType类型坐标)在代数扩展到较高维度的情况下需要进行高强度的代数计算因而没有被提供,which explains the need for a new point type。
一个面向这一新类型的一致的判定和构造集合由本包提供。
General Functionalities
The spherical kernel currently implements a set of fundamental functionalities like intersection, comparisons, inclusion, etc. More might be provided in the future, as long as only algebraic numbers of degree two are used.
spherical kernel当前提供了一个基本函数集的实现:交集(intersection),比较(comparisons),包含(inclusion)等。更多的功能新在未来提供。
Functionalities Relative to a Sphere
The interface of the underlying objects is extended by providing additional operations that make sense only if the objects are considered on the same sphere. For example, the result of the comparison of the cylindrical or spherical coordinates of two points is well-defined only when looking at them on a given common sphere. The presentation of these operations requires the following definitions:
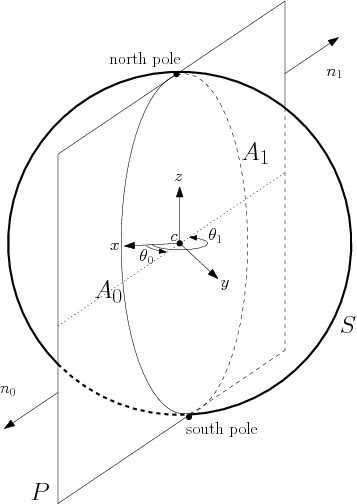
Coordinate system. Let consider a sphere with center c and radius r. Using the Cartesian frame centered at c, we define a cylindrical coordinate system (θ,z) on that sphere, with θ∈[0,2π) and z∈[−r,r]. θ is given in radian and measured in the xy-plane around the z-axis, starting from x>0, y=0. The z-extremal points of a sphere are its North and South poles defined as (θ,r) and (θ,−r) respectively, for any value of θ. Observe that each point on the sphere different from a pole corresponds to a unique pair (θ,z).
Definition of a meridian. Given a sphere and its associated cylindrical coordinate system, a meridian of that sphere is a circular arc consisting of the points having the same theta-coordinate (the poles are the end points). A plane containing the two poles of that sphere defines two meridians, one on each side of the line passing through the poles. A vector M whose direction is different from that of the latter line defines a unique meridian on that sphere. The plane of that meridian is defined by the direction of M and the two poles. The sense of M disambiguates the choice among the pair of meridians thus defined. On Figure 11.1, the normal vectors n0 and n1define two meridians of S: the circular arcs A0 and A1 respectively.
下层对象的接口提供了附加的操作,这些操作只有在对象是同一个球体时才有效。如,2个柱面或球面的点的坐标的比较结果是良好定义的,当且仅当将两个点放在一个给定的共同球上。这些操作的使用需要下面的定义:
坐标系统(Coordinate system)。我们考虑一个球体,其圆心是c 半径是 r。使用笛卡尔坐标并将其中心定为 c,我们在球上定义柱面坐标系统(θ,z),其中 θ∈[0,2π) 且 z∈[−r,r]。θ由弧度给出且在xy面上上围绕z轴测定(由x>0, y=0起始)。 球的z极点分别是其北极 (θ,r)和南极点(θ,−r)。对于任意的角度 θ(即θ固定时). 观察球面上每个点的不同在于唯一的对(θ,z)确定的极。
子午线定义(Definition of a meridian.)。给定一个球体和它相应的柱面坐标系统,球的一个子午线是一个包含了所有相同 θ 的点的一个圆弧(极点是其端点)。一个包含两极的平面定义了两个子午线,分别在两个极点连线的两侧。
一个向量M,其方向与前面定义的直线方向不同,它定义了唯一的球体子午线。子午线所在平面由M的方向和两个极点确定。M的定义消除了在选择两个子午线时的歧义。在图11.1中,正定(mormal) 的向量n0和n1定义了S的两个子午线:分别是圆弧A0和A1。
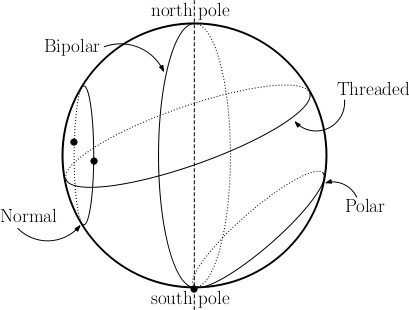
Types of circles on a sphere. Given a sphere, a circle on that sphere is termed polar if it goes through only one pole, bipolar if it goes through the two poles of that sphere and threaded if it separates the sphere into two connected components, each containing one pole. Any other circle is termed normal. These definitions are illustrated on Figure 11.2.
图11.1定义了S球体的两个子午线。通过S两个极点的平面P和S的交集是一个圆。A0和A1分别是S的两个子午线,它们由两个极点分开。这两个子午线的θ坐标分别是θ0 和 θ1=θ0+π。
球上的圆的类型(types of circles on a sphere)。如果一个圆只通过一个极点,则被称为极圆(polar );如果它通过两个极点,则为双极圆(bipolar )。如果它将球体分割为两个连接的部分,每个部分包含一个极点,则为间线圆(threaded );其他所有的圆被称为普通线(normal)。图11.2给出了几种线。
θ-extremal points. Given a sphere one has: a θ-extremal point of a normal circle is a point of tangency between the circle and a meridian anchored at the poles of that sphere. Each normal circle defines two such points; the θ-extremal point of a polar circle is the pole the circle goes through. No such point is defined on a bipolar or a threaded circle. These definitions are illustrated on Figure 11.2. Notice that the θ-extremal points should not be confused with the endpoints of an arbitrary arc on a sphere.
The θ-coordinate of a θ-extremal point of a normal circle on a sphere is well defined. For a polar circle on a sphere, the plane containing the two poles and which is tangent to that circle contains two different meridians. The θ-values of these meridians are the two θ-coordinates associated to the same θ-extremal point of a polar circle.
θ-monotone circular arcs. An arc on a sphere is said to be θ-monotone if any meridian on that sphere intersects that arc in at most one point. With this definition, a circular arc on a threaded circle is always θ-monotone, and an arc on a polar or normal circle is θ-monotone if it does not contain a θ-extremal point, unless it is an endpoint. No such arc is defined on a bipolar circle.
θ-外部点(θ-extremal points.)。给定一个球体,它有:一个普通圆的θ-外部点是该圆与一个子午线之间的切点。每个普通圆定义了两个这样的点;极圆(polar )的θ-外部点是该圆所经的极点。双极圆和间线圆(threaded )没有这个点定义。注意:不要将θ-外部点(θ-extremal points.)与球上的一个弧的端点相混淆。
一个普通圆(normal circle)θ-外部点(θ-extremal points.)的θ-坐标(θ-coordinate)是定义良好的。对一个球上极圆(polar ),与其相切、且过两极的的平面包含两个子午线。这两个子午线的θ-坐标值就是这个单θ-外部点的两个θ-坐标。
θ-单调圆弧(θ-monotone circular arcs. )。如果一个球上的所有子午线与一个弧最多只有一个交点,则我们说这个弧是θ-单调圆弧。基于这一定义 ,我们发现所有 间线圆是θ-单调圆弧,而如果一个极圆(polar )或一个普通圆上的弧如果不含θ-外部点则它是θ-单调圆弧,除非它是一个端点。在双极圆上则没有θ-单调圆弧的概念定义。
Software Design
The design of Spherical_kernel_3 is similar to the design of Circular_kernel_2 (see Chapter 2D Circular Geometry Kernel).
It has two template parameters:
- the first parameter must model the CGAL three dimensional
Kernelconcept. The spherical kernel derives from it, and it provides all elementary geometric objects like points, lines, spheres, circles and elementary functionality on them. - the second parameter is the algebraic kernel, which is responsible for computations on polynomials and algebraic numbers. It must model the concept
AlgebraicKernelForSpheres. The robustness of the package relies on the fact that the algebraic kernel provides exact computations on algebraic objects.
The 3D spherical kernel uses the extensibility scheme presented in the kernel manual (see Section Extensible Kernel). The types of Kernel are inherited by the 3D spherical kernel and some types are taken from the AlgebraicKernelForSpheres parameter. Spherical_kernel_3 introduces new geometric objects as mentioned in Section Spherical Kernel Objects.
In fact, the spherical kernel is documented as a concept, SphericalKernel and two models are provided:
Spherical_kernel_3<Kernel,AlgebraicKernelForSpheres>, the basic kernel,- and a predefined kernel
Exact_spherical_kernel_3.
Spherical_kernel_3定义与的 Circular_kernel_2定义相似(see Chapter 2D Circular Geometry Kernel)。
它有两个模板参数:
第一个参数必须是CGAL 3D Kernel 概念的一个模型。spherical kernel 由它继承而来,它提供了所有基本的几何对象,如点,线,球体,圆和操作这些对象的基本的函数。
第二个参数是代数内核(algebraic kernel),负责计算多项式和代数数。它必须是 AlgebraicKernelForSpheres概念的模型。本包的健壮性依赖于代数内核提供对代数对象的精确的计算。
3D spherical kernel 使用 kernel 手册中给出的可扩展模型((see Section Extensible Kerne)。3D spherical kernel继承了 Kernel 的类型,且有些类型取自于AlgebraicKernelForSpheres参数。Spherical_kernel_3 引入Spherical Kernel Objects一藬中提到的新的几何对象。
实际上,spherical kerne被载明是一个概念,其中提供SphericalKernel和两个模型:
(1)Spherical_kernel_3<Kernel,AlgebraicKernelForSpheres>,即基本模型
(2)一个预先定义的内核:Exact_spherical_kernel_3
Examples
The first example shows how to construct spheres and compute intersections on them using the global function.
第一个例子演示如何使用全局函数构造球体并计算它们的交集
File Circular_kernel_3/intersecting_spheres.cpp
The second example illustrates the use of a functor.
第二个例子演示函子的使用。
File Circular_kernel_3/functor_has_on_3.cpp
The third example illustrates the use of a functor on objects on the same sphere. The intersection points of two circles on the same sphere are computed and their cylindrical coordinates are then compared.
第三个例子演示在同一个球体上的对象上使用函子。计算同一个球体上的两个弧的交点并比较它们的柱面坐标。
File Circular_kernel_3/functor_compare_theta_3.cpp
Design and Implementation History
This package follows the design of the package 2D Circular Geometry Kernel).
Julien Hazebrouck and Damien Leroy participated in a first prototype.
The first version of the package was co-authored by Pedro Machado Manhães de Castro and Monique Teillaud, and integrated in CGAL 3.4. Frédéric Cazals and Sébastien Loriot extended the package by providing functionalities restricted on a given sphere [1].
Sylvain Pion is acknowledged for helpful discussions.
This work was partially supported by the IST Programme of the 6th Framework Programme of the EU as a STREP (FET Open Scheme) Project under Contract No IST-006413 (ACS - Algorithms for Complex Shapes).