T1:

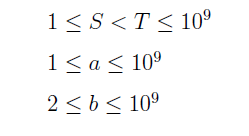
分析:
写出s变换的式子:(((s+a)*b+a)*b)……
将式子化简:
又可以把m写成: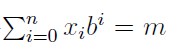
也就是将m拆成一个b进制数,每次贪心地使 i 大的时候xi尽量大,那么就可以花费最小次数凑出m。

#include<bits/stdc++.h> using namespace std; #define ri register int #define ll long long int main() { freopen("a.in","r",stdin); freopen("a.out","w",stdout); ll S,T,a,b; scanf("%lld%lld%lld%lld",&S,&T,&a,&b); ll nowb=1,n=0,ans=(1ll<<62); while(1){ ll t=T-nowb*S; if(t<0) break; if(t%a==0){ ll tot=n,m=t/a; ll bb=nowb; while(m){//把m拆成b进制数 tot+=m/bb; m%=bb; bb/=b; } ans=min(ans,tot); } n++; nowb=nowb*b; } printf("%d ",ans==(1ll<<62) ? -1 : ans); } /* 10 28 4 2 4685 56756 32764 43856 6 207 5 3 10000 100000000 3 5 179 222963 59 384 */
T2:


分析:
很显然可以二分一个答案,考虑怎么check。
首先将不满足条件的提出来,对于长的边,想办法将其缩短,但有一种错误的想法:对不满足的点对取交,然后将点对设在交集处。
为什么是错的呢?
比如下面这一组数据:
1 2 3 4 5 6 7
2 7
3 6
如果按照刚刚那样做的话,会将点对设在3 6处(交集),输出2
而正确的设法应该在2 6设,3可以先走到2再走到6,输出1
下面考虑正解:
设最终设定的两个点为u,v。
任意一个点对x,y的贡献是这两种间取min:1. y-x 2. abs(x-u)+abs(y-v)
然后答案就是所有的取max
我们已经二分了一个mid,对于前一种小于等于mid的可以直接跳过,但后一种未知u,v,所以应该怎么处理呢?
abs(x-u)+abs(y-v)<=mid 是曼哈顿距离的形式。
可以将(x,y)看做平面上的一个点,所有不超过mid的范围即平面上的一个菱形,只需要对每一个点对做出一个菱形后求交即可。
但菱形不好求交,转换成正方形:坐标这样转换(x,y)->(x-y,x+y)
为什么呢?相当于将菱形的四条边向左边延长
像这样:
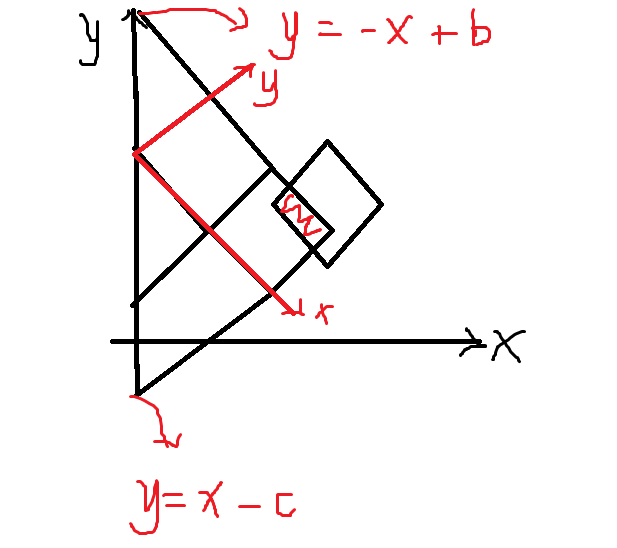
可以看到有两个解析式,将其移项即可知道x,y的转换关系了。
那为什么不考虑b和c分别是什么呢?
因为只需要一种映射关系,判断他们能不能有交就可以了,具体交是多少不需要知道。
然后用lx和rx分别记录一下交的范围,判断是否不符合的都有交即可。

#include<bits/stdc++.h> using namespace std; #define N 100005 #define ri register int #define inf (1<<30) int L[N],R[N],n,m; struct node { int l,r; }; void work(node &x) { int ll=x.l,rr=x.r; x.l=ll-rr; x.r=ll+rr;//将菱形转换成正方形 } bool check(int mid) { int lx=-inf,rx=inf,ly=-inf,ry=inf; for(ri i=1;i<=m;++i){ if(R[i]-L[i]<=mid) continue; node x=(node){L[i]+mid,R[i]}; node y=(node){L[i]-mid,R[i]}; work(x); work(y); lx=max(lx,y.l),rx=min(rx,x.l);//求交 lx rx分别表示x轴上的有交的范围 ly ry同理 ly=max(ly,y.r),ry=min(ry,x.r); if(lx>rx || ly>ry) return false; } return true; } int main() { freopen("b.in","r",stdin); freopen("b.out","w",stdout); scanf("%d%d",&n,&m); int mx=0; for(ri i=1;i<=m;++i) scanf("%d%d",&L[i],&R[i]),mx=max(R[i]-L[i],mx); int l=0,r=mx+1,ans=inf; while(l<r){ int mid=(l+r)>>1; if(check(mid)) r=mid,ans=min(ans,mid); else l=mid+1; } printf("%d ",ans); } /* 6 2 1 5 2 6 9 4 1 4 1 8 5 6 4 8 5 17 1 4 1 1 1 1 1 3 3 4 3 4 1 4 2 2 1 4 2 3 2 4 1 3 3 4 1 3 1 2 1 4 1 4 */
T3:


分析:
有一个很重要的性质:

有了这个性质之后直接二分一个k,先让小B交换完k轮,小A再去交换,看总次数是否小于等于k即可。
任意交换数组中两个元素,使得有序的最小交换次数 求法:
4 3 1 2 5
先让4和本该属于1位置的1交换,用mp记录1的位置,直接交换即可。
注意交换后mp[4]的值会被改变!!

#include<bits/stdc++.h> using namespace std; #define ri register int #define N 400005 int a[N],s[N],x[N],y[N],n,mp[N],vis[N]; bool check(int k) { memcpy(a,s,sizeof(s)); memset(vis,0,sizeof(vis)); for(ri i=1;i<=k;++i) swap(a[x[i]],a[y[i]]); int cnt=0,i=0; for(ri i=0;i<n;++i) mp[a[i]]=i; for(ri i=0;i<n;++i) if(a[i]!=i){//每次找到一个位置不符合的 把后面应该属于这个位置的交换过来 int xx=a[i],yy=a[mp[i]]; swap(a[i],a[mp[i]]),cnt++; mp[xx]=mp[i];//!!!注意mp也换了位置!! } return cnt<=k; } int main() { freopen("c.in","r",stdin); freopen("c.out","w",stdout); scanf("%d",&n); for(ri i=0;i<n;++i) scanf("%d",&s[i]); for(ri i=1;i<=n*2;++i) scanf("%d%d",&x[i],&y[i]); int l=0,r=2*n+1,ans; while(l<r){ int mid=(l+r)>>1; if(check(mid)) ans=mid,r=mid; else l=mid+1; } printf("%d ",ans); } /* 3 1 0 2 1 2 0 2 0 0 0 1 0 2 1 2 */
