衡量算法效率的两种方法
- 事后分析法
- 事前分析法(估算)
1、事后分析法
使用计算机内部的计时器功能(节拍),但是有些算法可能运行下来,也不足一个节拍,故可以采用多次运行的策略,达到预期的效果。
缺点
- 必须先多次运行依据算法编制的程序
- 时间统计量依赖于计算机的软硬件环境
2、事前分析法
与算法执行时间相关的影响因素
- 算法策略
- 问题规模
- 所使用的语言
- 编译器产生代码的质量
- 机器运行的速度
抛弃语言、编译器、运行机器的差异,我们知道前两者是我们分析算法效率的有效途径。
算法时间的度量
运行时间 = ∑算法中每条执行语句的执行时间
运行时间 = ∑(频度 ∗ 语句执行一次所需的时间)
若设每条语句执行的时间一样
运行时间 = ∑(每条语句重复执行的次数)
举个例子,下面有三个算法。
1、执行了n+1次
int i, sum = 0, n = 100; // 执行1次 for( i=1; i <= n; i++ ) { sum = sum + i; // 执行n次 }
2、执行了2次
int sum = 0, n = 100; // 执行1次 sum = (1+n)*n/2; // 执行1次
3、执行了2n2+1次
int i, j, x=0, sum=0, n=100; // 执行1次 for( i=1; i <= n; i++) { for( j=1; j <= n; j++ ) { x++; // 执行n2次方次 sum = sum + x; // 执行n2次方次 } }
然而,我们只需要选出对所研究的问题来说是基本操作的语句,以其在算法中重复执行的次数来作为衡量算法运行时间的衡量准则。算法执行时间与基本操作的执行次数之和成正比!
则算法1,可以看成执行了n次,算法2为1次,算法3为n2次。如下图

程序运行的好坏依赖于算法的策略和输入的规模。换句话说,衡量算法效率的指标就是随着问题规模的增大,算法的运行时间会处于哪个量级。
那么如何来比较算法之间的量级呢?
通过几个问题来分析一下
问题一:假设两个算法的输入规模都是n,算法A要做2n+3次操作,B要做3n+1次操作,试比较算法A和算法B的效率。

当n = 1时,算法A1是不如算法B1的,当n = 2时,两者效率是相同的,当n > 2时,A1算法就优于B2算法了。通过分析也知道,自此,A1与B1的差距变大了,总体上A1是优于B1的。
概念
函数的渐近增长:给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的n>N,f(n)总是比g(n)大,那么,我们说f(n)的增长渐近快于g(n)。
从问题一的分析可以发现,随着n的增大,常数项+3和+1并不会影响最终的增长变化。于是我们得出结论1,即可以忽略加法常数。
问题二:假设两个算法的输入规模都是n,算法C要做4n+8次操作,D要做2n2+1次操作,试比较算法C和算法D的效率。

我们发现由于指数的差距,就算去掉与最高项相乘的常数和其他次要项,两者的结果还是没有改变,随着n的增大,E2还是远远小于D2。所以有结论2,与最高项相乘的常数并不重要,可以忽略。
问题三:假设两个算法的输入规模都是n,算法E是2n2+3n+1,算法F是2n3+3n+1 ,试比较算法E和算法F的效率。

可以很明显的看到指数较大的函数增长很快。所以结论三是最高项的指数非常重要,指数越大,增长速度越快。
问题四:假设三个算法的输入规模都是n,算法G是2n2,算法H是3n+1,算法I是 2n2+3n+1。,试比较算法G、H和算法I的效率。
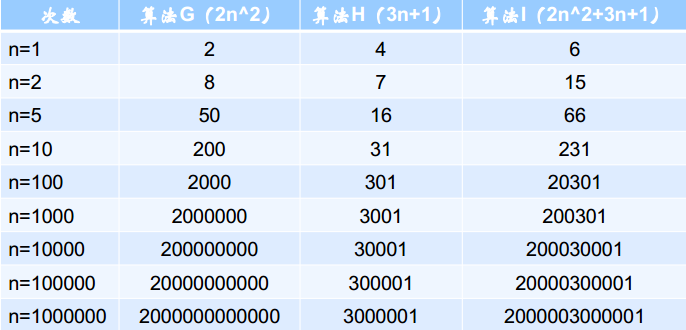
当n很大时,H已经无法和G比较了,更别说 I 算法了,所以结论四是判断一个算法的效率时,函数的常数项和其他次要项可以忽略,应该关注最高次的项。
算法时间复杂度
- 在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。
- (渐进)时间复杂度 T(n) = O( f(n) ), n-问题规模
表示随问题规模n的增大,算法执行时间的增长率/阶和f(n)的增长率/阶相同。
- 其中f(n)是问题规模n的某个函数。
- 大O符号(英语:Big O notation)是用于描述函数渐近行为的数学符号,也可理解为Order(阶)的缩写。
那如何来分析算法的(渐近)时间复杂度,即推导大O阶呢?三个规则如下:
1、用1取代运行时间内的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高项存在且不是1,除去与最高项相乘的常系数。
举几个例子
常数阶
int a = 100; //执行一次 int b = 200; //执行一次 int sum = a + b; //执行一次 printf("%d ", sum); //执行一次
每行执行一次,共4次,f(n) = 4,即T(n) = O(4),算法的时间复杂度为O(1)。(规则1)
线性阶
void func() { int i, sum = 0; //执行一次 for (i = 0; i <= 100; i++) { sum += i; //执行n次 } printf("%d ", sum); //执行一次 }
程序段的执行次数为1+n+1,f(n) = n + 2,T(n) = O(n),算法的时间复杂度为O(n)(规则2)
平方阶
void func() { int i, j, n = 100; for( i=0; i < n; i++ ) { for( j=0; j < n; j++ ) { printf(“I love China. ”); } } }
程序段的执行次数为n*n+1,f(n) = n*n,T(n) = O(n2),算法的时间复杂度为O(n2)(规则2)
void func() { int i, j, n = 100; for( i=0; i < n; i++ ) { for( j=i; j < n; j++ ) { printf(“I love China. ”); } } }
程序段的执行次数为1+n(n+1)/2 = n2/2+n/2,f(n) = n*n,T(n) = O(n2) ,算法的时间复杂度为O(n2)。(规则2、3)
对数阶
void func() { int i = 1; do { i *= 2; } while (i < n); }
按照前面的知识,可知程序循环了f(n)次,2f(n) = n,f(n) = log2n,T(n) = O(log2n) ---> T(n) = O(log n)(规则2、3,对数的底数为2并不是分析问题的关键,关键是对数级别)
更多


算法空间复杂度
- 空间复杂度: 因算法引入的额外辅助空间
- (渐进)空间复杂度: S(n) = O(f(n))
- 若所需额外空间相对于输入数据量来说是常数,则称此算法为原地工作
- 若所需存储量依赖于特定的输入,则通常按最坏情况考虑
常用的空间复杂度量级有O(1),O(n),O(n2).
当我们定义了一个普通的整形变量时,例如(int i = 1;),此时的空间复杂度就为O(1),当定义一个一维数组时,空间复杂度就为O(n),那最后一个复杂度可想而知了,会对应什么。