前言
[摘录于网络,已经加以修订,感谢原作者]有人说,解几何题“得辅助线者得天下”。这句话虽然有些夸张,但是学好添加辅助线是我们快速解题的重要途径,那么辅助线应该如何添加呢?
使用原因
解证几何问题的基本思路就是要利用已知几何条件求得所求几何关系。这往往需要将已知条件与所求条件集中到一个或两个几何关系十分明确的简单的几何图形之中。如一个三角形(特别是直角三角形、等腰三角形),一个平行四边形(特别是矩形、菱形、正方形),一个圆,或两个全等三角形,两个相似三角形之中。这种思路可称为条件集中法。
为了达到条件集中的目标,我们需要将远离的、分散的已知条件和所求条件,通过连线、作线、平移、翻转、旋转等方法来补全或构造一个三角形、一个平行四边形、一个圆、或两个全等三角形、两个相似三角形,便于运用这些图形的几何关系(性质定理)解题,这就需要添加辅助线。
考量原则
添加什么样的辅助线,总的来说,由以下三方面决定:
⑴.由所求决定:问什么,先要作什么。
⑵.由已知决定:已知什么,作出什么,并为充分运用已知条件提供的性质定理添加辅助线。
⑶.由条件集中的需要决定:为补全或构造几何关系十分明确的一个三角形、一个平行四边形、一个圆,或两个全等三角形、两个相似三角形而添加辅助线。
分类细述
添加辅助线的目的,就是将题目中的已知条件之间建立联系。做辅助线的方法多种多样,具体题目要具体分析,但是也有其相对固定的套路。以下的总结的很全面,希望细细品味。
(Ⅰ).在三角形中如何添加
①等腰Δ:常连底边上的中线或高或顶角的平分线(构造两个全等的直角Δ,或便于运用等腰Δ三线合一的性质.)
②直角Δ斜边上有中点:连中线(构造两个等腰Δ,或便于运用直角Δ斜边上的中线的特殊性质.)或做斜边的中垂线,构造等腰三角形。
③斜Δ[锐角和钝角三角形的统称]有中点或中线:连中线(构造两个等底同高的等积Δ);
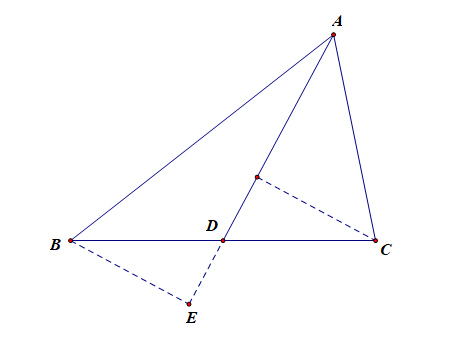
或自左右两顶点分别作中线的垂线(构造两个全等直角三角形);
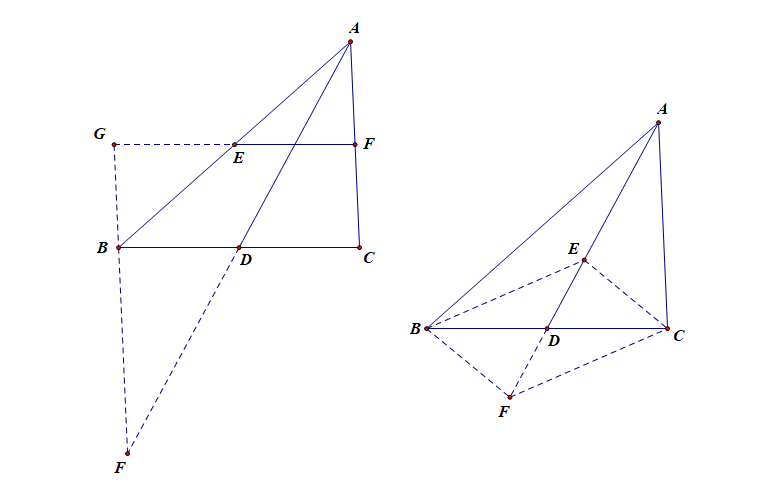
或连中位线、或过一中点作另一边的平行线(构造两个相似比为1:2的相似Δ,或便于运用Δ中位线定理);

或延长中位线以补全为一个平行四边形;或延长中线的一倍以构造两个全等Δ;或延长中线的(cfrac{1}{3}),以构造两个全等Δ或补全为一个平行四边形。
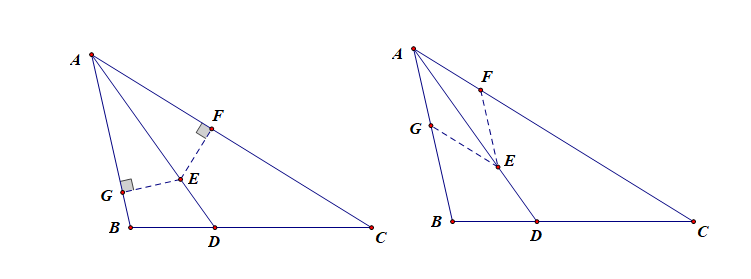
④有角平分线:过其上某一交点作角两边的垂线(构造两全等的直角Δ)或一边或两边的平行线(构造一个或两个等腰Δ或一菱形).
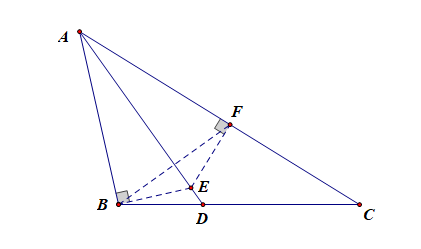
⑤有角平分线:在此角的一边上自顶点取一段等于另一边并作相关连线(构造两个全等Δ)
⑥有角平分线遇垂线:常延长垂线(构造等腰Δ).
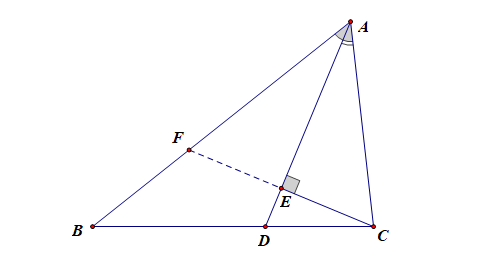
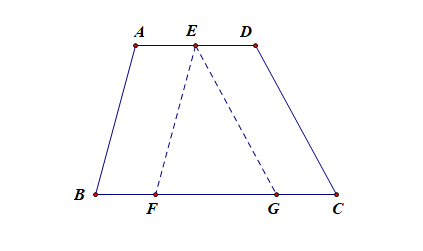
(Ⅱ).在梯形中如何添加
①延长两腰交于一点(构造两相似Δ),
②由小底的一端作一腰的平行线(构造一集中有两腰及上下两底差的Δ和一平行四边形).
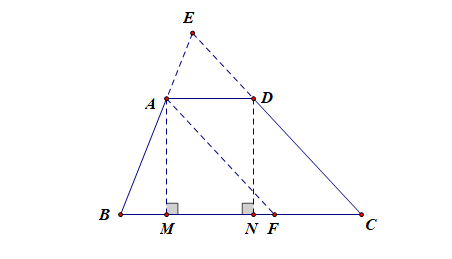
③由小底的两端作大底的垂线(构造两直角Δ和一矩形).
④有对角线时:由小底的一端作另一对角线的平行线(构造一集中有两对角线及上下两底和的Δ和一平行四边形).
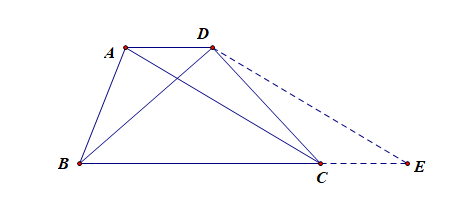
⑤连小底一端与另一腰中点并与大底的延长线相交(构造两全等Δ及一与梯形等高等积的Δ).
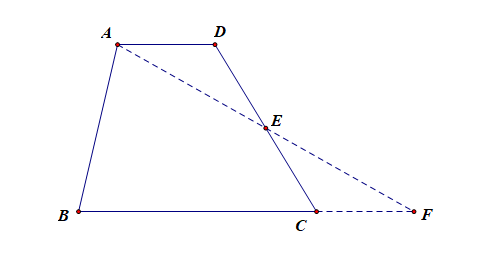
⑥过一腰的中点作另一腰的平行线(构造两全等Δ及与梯形等积的平行四边形).

⑦过小底的中点分别作两腰的平行线(构造一集中有两腰及上下两底差的Δ和两个平行四边形).
(Ⅲ).在圆中如何添加
①有弦:连过弦端点的半径,连垂直于弦的直径或弦心距(构造直角Δ,便于运用垂径定理、勾股定理、锐角三角函数解题);或作过弦一端点的切线及相关的圆心角、圆周角(便于运用弦切角定理).

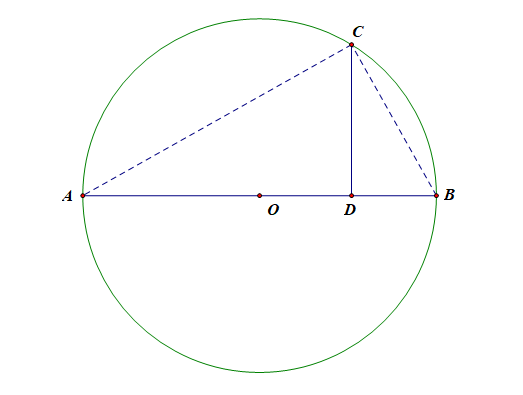
②有直径及垂直直径的弦或半弦,连结弦与直径的端点(构造三个相似的直角Δ,便于运用直角Δ的性质及射影定理).
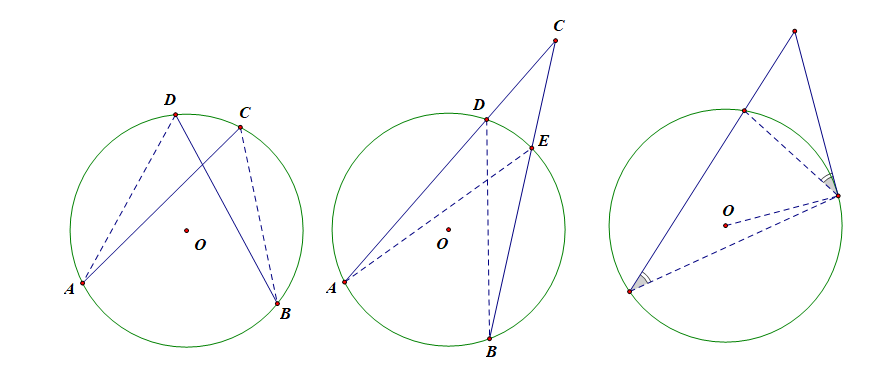
③有圆内接四边形:连对角线(构造较多相等的圆周角);或延长四边形的某一边(构造与内对角相等的外角).

④圆外有切线:连过切点的半径或直径(构造垂直关系);或作过切点的弦及相关的圆心角、圆周角(便于运用弦切角定理).

⑤圆外有两条相交切线:连过切点的半径,并作切线交点与圆心的连线(构造两全等的直角三角形);或作过交点和加以的割线(便于运用切线割线定理);或连结两切点(构造一等腰Δ、三对全等的直角Δ、被切线交点与圆心的连线垂直平分的弦,便于运用等腰Δ、直角Δ、全等Δ以及射影定理).

⑥有相交弦或相交于圆外的割线[或切线]:连结不同弦的端点或不同割线在圆上的交点(构造相似Δ,便于运用比例线段及Δ外角定理).
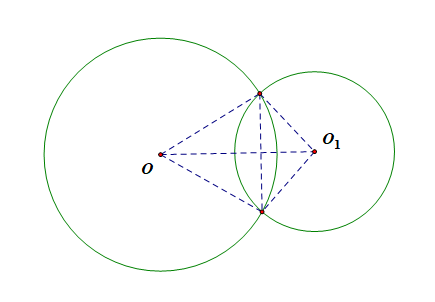
⑦两圆相交:作连心线、公共弦,甚至两圆心到公共弦两端点的连线(构造两等腰Δ、补全一筝形,便于运用连心线垂直平分公共弦的定理).
⑧两圆外切:作连心线及内、外公切线、连切点、连半径(构造一集中有两条弦及外公切线长的直角Δ、一集中有两圆半径、半径之和及外公切线长的直角梯形).

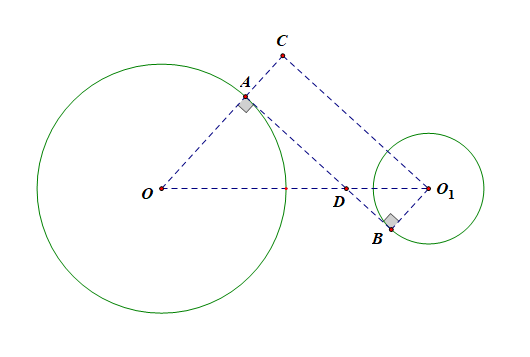
配图说明:(angle OAC=angle OCA),(angle O_1BC=angle O_1CB)(半径相等),
(angle CAD=angle DCA=cfrac{1}{2}angle COA)(弦切角定理),(angle DBC=angle DCB=cfrac{1}{2}angle CO_1B)(弦切角定理),
由(angle CAD+angle DCA+angle DCB+angle DBC=180^{circ})(三角形内角和定理)
可得(angle ACB=90^{circ}),故( riangle ACB)为(Rt riangle),且点(D)为斜边(AB)的中点。且(AD=CD=BD)。
⑨两圆内切:作连心线及外公切线(便于运用连心线与公切线的垂直关系).

⑩两圆外离:作连心线及个公切线或内公切线,并过小圆圆心作公切线的平行线(构造一集中连心线长、公切线长、两圆半径差或和的直角Δ).

典例剖析

【高中解法】由( an15^{circ}=cfrac{AB}{BC}),则(AB=BCcdot an15^{circ}=2(2-sqrt{3})).
【初中解法】如图所示,取(AC)的中点(E),过点(E)做线段(AC)的垂线,交(BC)于点(D),则可知(DC=DA),
故(angle DCA=angle DAC=15^{circ}),则(angle BDA=30^{circ}),
在(Rtangle ABD)中,设(AB=x),则(AD=2x),且(CD=AD=2x),(BD=sqrt{3}x),
由已知,(BC=2=BD+CD=sqrt{3}x+2x),变形为((2+sqrt{3})x=2),
故(x=cfrac{2}{2+sqrt{3}}=2(2-sqrt{3}));即(AB=2(2-sqrt{3})).


理由:同底等高;两平行线间的距离相等;
(2).[初中探究]如图所示的多边形(ABCDE),若想过点(E)作一条直线(EF)(其中点(F)位于直线(BC)上),使得直线(EF)左侧的四边形(ABFE)面积和多边形(ABCDE)的面积相等,请写出设计方案,并说明理由。
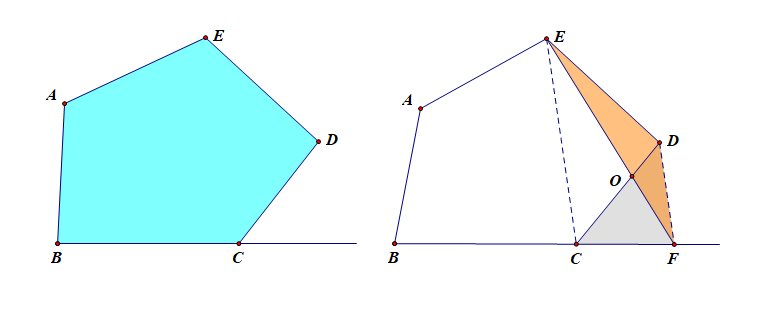
做法:连结(EC),过点(D)做(DF//EC)交(BC)于(F),连结(EF),则直线(EF)为所求;
说明:由于(S_{多边形ABCDE}=S_{多边形ABCOE}+S_{ riangle EOD}),(S_{四边形ABFE}=S_{多边形ABCOE}+S_{ riangle COF}),
又由于(EC//DF),由同底等高的缘故可知,(S_{ riangle DFE}=S_{ riangle DFC}),
又由于(S_{ riangle DFE}=S_{ riangle DFO}+S_{ riangle DOE}),(S_{ riangle DFC}=S_{ riangle DFO}+S_{ riangle COF}),
故(S_{ riangle DOE}=S_{ riangle COF}),故(S_{多边形ABCDE}=S_{四边形ABFE}),
即直线(EF)为符合题意的直线。

分析:做出如图所示的辅助线,由(angle PDE)的两个余角分别为(angle EDF)和(angle BDP),故(angle EDF=angle BDP),
故( riangle EDFsim riangle BDP),又由于斜边(BD=BE),故( riangle EDFcong riangle BDP),
同理可证,( riangle EDFcong riangle EAN),
或者理解为将(Rt riangle EDF)绕点(D)顺时针旋转(90^{circ})得到(Rt riangle BDP),
将(Rt riangle EDF)绕点(E)逆时针旋转(90^{circ})得到(Rt riangle EAN),
这样(S_2=S_{ riangle BCP}-S_{ riangle BDP}=cfrac{1}{2} imes 4 imes(3+3)-cfrac{1}{2} imes 4 imes 3=6);
(S_1=S_{ riangle AHN}-S_{ riangle EAN}=cfrac{1}{2} imes 3 imes(4+4)-cfrac{1}{2} imes 4 imes 3=6);
又(S_3=cfrac{1}{2} imes 3 imes 4=6);故(S_1+S_2+S_3=18);
记忆口诀
人说几何很困难,难点就在辅助线。辅助线,如何添?把握定理和概念。
还要刻苦加钻研,找出规律凭经验。题中有角平分线,可向两边作垂线。
线段垂直平分线,可向两端把线连。三角形中两中点,连结则成中位线。
三角形中有中线,延长中线同样长。成比例,证相似,经常要作平行线。
圆外若有一切线,切点圆心把线连。如果两圆内外切,经过切点作切线。
两圆相交于两点,一般作它公共弦。是直径,成半圆,想做直角把线连。
作等角,添个圆,证明题目少困难。辅助线,是虚线,画图注意勿改变。
图中有角平分线,可向两边作垂线。也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。三角形中有中线,延长中线等中线。
平行四边形出现,对称中心等分点。梯形里面作高线,平移一腰试试看。
平行移动对角线,补成三角形常见。证相似,比线段,添线平行成习惯。
等积式子比例换,寻找线段很关键。直接证明有困难,等量代换少麻烦。
斜边上面作高线,比例中项一大片。半径与弦长计算,弦心距来中间站。
圆上若有一切线,切点圆心半径连。切线长度的计算,勾股定理最方便。
要想证明是切线,半径垂线仔细辨。是直径,成半圆,想成直角径连弦。
弧有中点圆心连,垂径定理要记全。圆周角边两条弦,直径和弦端点连。
弦切角边切线弦,同弧对角等找完。要想作个外接圆,各边作出中垂线。
还要作个内接圆,内角平分线梦圆。如果遇到相交圆,不要忘作公共弦。
内外相切的两圆,经过切点公切线。若是添上连心线,切点肯定在上面。
要作等角添个圆,证明题目少困难。辅助线,是虚线,画图注意勿改变。
假如图形较分散,对称旋转去实验。基本作图很关键,平时掌握要熟练。
解题还要多心眼,经常总结方法显。切勿盲目乱添线,方法灵活应多变。
分析综合方法选,困难再多也会减。虚心勤学加苦练,成绩上升成直线。