事故发生在上周的牛客比赛，我用某作业帮拍题AC了T1
于是我用同样方法做了今天的T2 推箱子, 取得4分的好成绩，还加了10多个特判
于是......我意识到不学数论是不行的， 那就先学一下扩展欧几里得吧
upd 2021.8.20 : 加了一些证明， 证明还是很重要的裴蜀定理
来看这么一个不定方程：ax + by = c ， 对于该方程， 当且仅当c为gcd(a, b)的倍数时， 方程有解。
证明方法，感兴趣读者可自行查阅更为详细的资料， 本文不再赘述。其实是我懒得证明
upd:口糊一个证明, 因为ax, by肯定是gcd的倍数,所以c一定是gcd的倍数，至于充分性：c是gcd倍数时一定有解， 这个可以直接用exgcd的转移做数学归纳法
扩展欧几里得
那么问题来了，如果我们不仅仅想要知道该方程是否有解，而且需要具体求出这些解该怎么办呢？
这时候，就需要用到扩展欧几里得了，显然：该算法是欧几里得的扩展版本，可以在求gcd的时候顺便求出一组可行解。
先来看看普通的gcd
int gcd(int a, int b) {
if (b == 0) return a;
return gcd(b, a % b);
}
我们先假设gcd函数在求出a,b的gcd同时， 还能求出一组(x, y)，使得ax+by=gcd(a, b)(注意这里不是=c)。
那么我们在执行gcd(a, b)时，会先递归调用 gcd(b, a%b)，并且求出一组x1, y1满足 b*x1 + (a%b)*y1 = gcd(b, a%b) .
显然gcd(b, a%b)==gcd(a, b), 所以又可以写成 b*x1 + (a%b)*y1 = gcd(a, b)
进一步，a%b =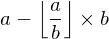 
, 带入得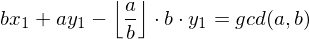
分别提出a, b：
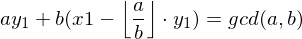
我们回到最开始，需要求出（x, y）使得 ax+by=gcd(a, b) ， 根据上式
x = y1 , y = x1-(a/b)*y1
这样就可以递归求解了，但还要考虑一下递归的边界， 由于递归的方式和gcd一样，所以先考虑一下gcd的边界。 gcd在b==0时返回, 此时 gcd(a, b) = a （因为b为0）。容易想到， a*1+b*0 = a = gcd(a, b), 所以这时我们直接返回即可，x=1, y=0。
详见代码
int exgcd(int a, int b, int &x, int &y) {
if(b == 0){
x = 1, y = 0;
return a;
}
int res = exgcd(b, a%b, x, y);//gcd的结果，同时得到（b, a%b）时的x，y
int l = x;
x = y; // x = y1
y = l - (a/b)*y; // y = x1 - (a/b)*y;
return res;
}
于是，我们就可以求出一组解 使得 ax+by=gcd(a, b)了。回到问题，我们要求的是 ax+by = c, 根据裴蜀定理，c为gcd(a, b)时才有解，否则直接特判无解。
c为gcd(a, b)倍数时, 我们要将等式右边变成c，将式子两边同时乘上 c/gcd(a, b) 即可，得到原式的一组解 x*gcd, y*gcd
如果仍不理解， 读者可根据上文手推一遍式子
求出所有整数解
然而这里只有一组解，我们想要得到的是所有整数解，所以扩展欧几里得并不能解决这个问题 ，不做了(大雾
我们可以将x加上一个b/gcd, 将y减去一个a/gcd，这样所得到的一组x,y仍是方程的解。
为什么呢？
a*x + b*y = c, 这是原式，分解开来
a*x ---> a*(x+b/gcd) ---> a*x + a*b/gcd 相当于增加了一个a*b/gcd;
b*x 同理---> b*y - a*b/gcd ; 相当于减少了一个a*b/gcd;
容易发现a*b/gcd 实际上就是a,b最小公倍数(lcm)，也就是说，加上一个lcm，又减小一个lcm,式子值不变，等式当然还是成立， 所以仍是方程的解。反复进行该操作，即可得到所有的解
upd: 这只是构造一组解， 没有证明为什么可以构造出所有解， 这里补上:
假设当前解为x, y， 那么如果要得到所有解， 我们可以尝试找到大于x的第一个解x1, 此时y为y1, 也就是说， 要找到最小的x1（x1 > x）使得等式成立 ax1+by1=ax+by, 我们设x2=x1-x, y2=y1-y, 也就是：a(x+x2)+b(y+y2)=ax+by，ax2=-by2，且x2最小，
也就是ax2最小，显然当ax2 = lcm(a, b) = by2时达到最小， 故可以得到所有解
总结一下求解的过程： 先求出一组解，其他解都可以表示为 x+t(b/gcd) , y+t(a/gcd), 枚举所有t即可求出所有解（注意！！！t可以为负数，读者请仔细思考）
这个方程肯定是有无限个解的， 所以题目只会让我们求出符合要求的解统计答案
a, b...可以为负数吗？
这个细节真的非常坑....
前面所看到的代码， 也就是大多数博客所讲到的，并不能处理负数！！！
可是，欧几里得并没有规定a，b, c一定是是正整数，这时该怎么办呢？
其实也不难想到，但一定要注意， 只要把a, b变成正的即可。
如果a是负数，可以把问题转化成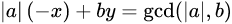 
（借一下百度百科的图）
然后求出所有解， 把每个解的x取负，即可得到原方程的解。
来看个题目 推箱子