bzoj5251: [2018多省省队联测]劈配
Description
一年一度的综艺节目《中国新代码》又开始了。
Zayid从小就梦想成为一名程序员,他觉得这是一个展示自己的舞台,于是他毫不犹豫地报名了。
题目描述
轻车熟路的Zayid顺利地通过了海选,接下来的环节是导师盲选,这一阶段的规则是这样的:
总共n名参赛选手(编号从1至n)每人写出一份代码并介绍自己的梦想。接着由所有导师对这些选手进行排名。
为了避免后续的麻烦,规定不存在排名并列的情况。
同时,每名选手都将独立地填写一份志愿表,来对总共m位导师(编号从1至m)作出评价。
志愿表上包含了共m档志愿。
对于每一档志愿,选手被允许填写最多C位导师,每位导师最多被每位选手填写一次(放弃某些导师也是被允许的)。
在双方的工作都完成后,进行录取工作。
每位导师都有自己战队的人数上限,这意味着可能有部分选手的较高志愿、甚至是全部志愿无法得到满足。节目组对”
前i名的录取结果最优“作出如下定义:
前1名的录取结果最优,当且仅当第1名被其最高非空志愿录取(特别地,如果第1名没有填写志愿表,那么该选手出局)。
前i名的录取结果最优,当且仅当在前i-1名的录取结果最优的情况下:第i名被其理论可能的最高志愿录取
(特别地,如果第i名没有填写志愿表、或其所有志愿中的导师战队均已满员,那么该选手出局)。
如果一种方案满足‘‘前n名的录取结果最优’’,那么我们可以简称这种方案是最优的。
举例而言,2位导师T老师、F老师的战队人数上限分别都是1人;2位选手Zayid、DuckD分列第1、2名。
那么下面3种志愿表及其对应的最优录取结果如表中所示:
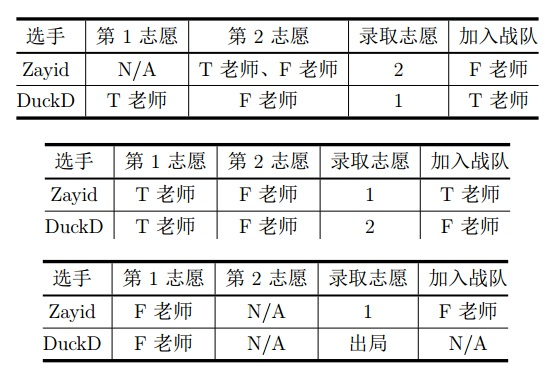
可以证明,对于上面的志愿表,对应的方案都是唯一的最优录取结果。
每个人都有一个自己的理想值si,表示第i位同学希望自己被第si或更高的志愿录取,如果没有,那么他就会非常沮丧。
现在,所有选手的志愿表和排名都已公示。巧合的是,每位选手的排名都恰好与它们的编号相同。
对于每一位选手,Zayid都想知道下面两个问题的答案:
在最优的录取方案中,他会被第几志愿录取。
在其他选手相对排名不变的情况下,至少上升多少名才能使得他不沮丧。
作为《中国新代码》的实力派代码手,Zayid当然轻松地解决了这个问题。
不过他还是想请你再算一遍,来检验自己计算的正确性。
Input
每个测试点包含多组测试数据
第一行2个用空格隔开的非负整数T;C,分别表示数据组数、每档志愿最多允许填写的导师数目。
接下来依次描述每组数据,对于每组数据:
第1行两个用空格隔开的正整数n;m。
n;m分别表示选手的数量、导师的数量。
第2行m个用空格隔开的正整数:其中第i个整数为bi。
Bi表示编号为i的导师战队人数的上限。
第3行至第n+2行,每行m个用空格隔开的非负整数:其中第i+2行左起第j个数为ai,j
ai,j表示编号为i的选手将编号为j的导师编排在了第ai,j志愿。特别地,如果ai,j=0,则表示该选手没有将该导师填入志愿表。
在这一部分,保证每行中不存在某一个正数出现超过C次(0可能出现超过C次),同时保证所有ai,j<=m。
第n+3行n个用空格隔开的正整数,其中第i个整数为Si
Si表示编号为i的选手的理想值。
在这一部分,保证Si<=m。
T<=5,m<=n<=200,Bi<=N
Output
按顺序输出每组数据的答案。对于每组数据,输出2行:
第1行输出n个用空格隔开的正整数,其中第i个整数的意义为:
在最优的录取方案中,编号为i的选手会被该档志愿录取。
特别地,如果该选手出局,则这个数为m+1。
第2行输出n个用空格隔开的非负整数,其中第i个整数的意义为:
使编号为i的选手不沮丧,最少需要让他上升的排名数。
特别地,如果该选手一定会沮丧,则这个数为i。
Sample Input
3 5
2 2
1 1
2 2
1 2
1 1
2 2
1 1
1 2
1 2
2 1
2 2
1 1
0 1
0 1
2 2
Sample Output
2 1
1 0
1 2
0 1
1 3
0 1
三组数据分别与【题目描述】中的三个表格对应。
对于第1 组数据:由于选手1 没有填写第一志愿,所以他一定无法被第一志愿录取,也就一定会沮丧。
选手2 按原排名就不沮丧,因此他不需要提升排名。
对于第2 组和第3 组数据:1 号选手都不需要提升排名。
而希望被第一志愿录取 的2 号选手都必须升到第1 名才能如愿。
题解
显然是网络流。
对于第一问,每个导师向汇点连一条容量(b_i)的边。然后依次考虑每个选手。对于某个选手,先从源点向他连一条容量为1的边,然后从高到低考虑每个志愿,每次向一个志愿中所有老师连边,判断流量是否增加,如果增加,答案即是这个志愿,否则再将这些边删掉。
对于第二问,由于(i)要实现梦想,因此他必须被前(s_i)志愿录取。我们把选手(i)与这些志愿中包含的导师全部进行连边。接着,我们依次检查第(1,…,i-1)名选手的志愿是否会发生变化:检查选手(k)时,只需要连(k)在第一小问中求出的答案志愿的边即可。如果检查到(k)时增广失败,则表示(i)不能完成梦想,一旦出现这种情况,则立刻可知(i)选手第二问的答案即为(i-k)。
很显然,这个算法的复杂度是(Ο(f(n,nC)n))的。其中(f(n,m))表示的是(Ο(n))个点(Ο(m))条边的二分图跑匹配的复杂度。用(dinic)算法最终的复杂度为(O(n^{2.5}C))。
需要注意的是,第一问中求出每个选手的答案之后,必须将非答案志愿中的边都删掉,否则会使边数达到(O(mnC))的级别。
代码
#include<bits/stdc++.h>
#define MAXN 410
#define INF 0x3f3f3f3f
namespace IO{
char buf[1<<15],*fs,*ft;
inline char gc(){return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;}
inline int qr(){
int x=0,rev=0,ch=gc();
while(ch<'0'||ch>'9'){if(ch=='-')rev=1;ch=gc();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=gc();}
return rev?-x:x;}
}using namespace IO;
using namespace std;
struct Edge{int t,next,v;}e[100010];
struct Data{int cnt,head[MAXN];Edge e[100010];}E[201];
int head[MAXN],cnt=1,S,T,d[MAXN];
inline void Add_Edge(int from,int to,int cap){
e[++cnt].t=to;e[cnt].next=head[from];head[from]=cnt;e[cnt].v=cap;
e[++cnt].t=from;e[cnt].next=head[to];head[to]=cnt;e[cnt].v=0;
}
inline void Init(){
cnt=1;
memset(head,0,sizeof(head));
}
queue<int>q;
inline bool BFS(){
memset(d,-1,sizeof(d));
q.push(S);d[S]=0;
while(!q.empty()){
int u=q.front();q.pop();
for(int i=head[u];i;i=e[i].next){
int v=e[i].t;
if(e[i].v&&d[v]==-1){
d[v]=d[u]+1;
q.push(v);
}
}
}
return d[T]!=-1;
}
int DFS(int u,int now){
if(u==T||!now)return now;
int f,flow=0;
for(int i=head[u];i;i=e[i].next){
int v=e[i].t;
if(d[v]==d[u]+1&&e[i].v&&(f=DFS(v,min(e[i].v,now-flow)))){
e[i].v-=f;e[i^1].v+=f;flow+=f;
if(flow==now)return flow;
}
}
if(!flow)d[u]=-1;
return flow;
}
int Q,C,N,M,b[MAXN],s[MAXN],ans1[210],ans2[210];
vector<int> a[210][210];
inline void Build(){
Init();
for(int i=1;i<=M;i++)Add_Edge(i+N,T,b[i]);
}
inline void Solve1(){
int last,now=0;
for(int i=1;i<=N;i++)Add_Edge(S,i,1);
for(int i=1;i<=M;i++)Add_Edge(i+N,T,b[i]);
E[0].cnt=cnt;
for(int i=1;i<=T;i++)E[0].head[i]=head[i];
for(int i=1;i<=cnt;i++)E[0].e[i]=e[i];
memset(ans1,0,sizeof(ans1));
for(int i=1;i<=N;i++){
last=now;
for(int j=1;j<=M;j++){
int siz=a[i][j].size();
for(int k=0;k<siz;k++){
Add_Edge(i,a[i][j][k],1);
}
while(BFS())now+=DFS(S,INF);
if(now>last){ans1[i]=j;break;}
cnt=E[i-1].cnt;
for(int k=1;k<=T;k++)head[k]=E[i-1].head[k];
}
if(!ans1[i])ans1[i]=M+1;
E[i].cnt=cnt;
for(int j=1;j<=T;j++)E[i].head[j]=head[j];
for(int j=1;j<=cnt;j++)E[i].e[j]=e[j];
}
}
inline void Solve2(){
int last,now;
for(int i=1;i<=N;i++){
if(ans1[i]<=s[i]){ans2[i]=0;continue;}
Build();now=0;ans2[i]=i;
Add_Edge(S,i,1);
for(int j=1;j<=s[i];j++){
int siz=a[i][j].size();
for(int k=0;k<siz;k++){
Add_Edge(i,a[i][j][k],1);
}
}
while(BFS())now+=DFS(S,INF);
for(int j=1;j<i;j++){
if(ans1[j]==M+1)continue;
last=now;
Add_Edge(S,j,1);
int siz=a[j][ans1[j]].size();
for(int k=0;k<siz;k++){
Add_Edge(j,a[j][ans1[j]][k],1);
}
while(BFS())now+=DFS(S,INF);
if(now==last){ans2[i]=i-j;break;}
}
}
}
int x;
int main(){
#ifndef ONLINE_JUDGE
freopen("mentor.in","r",stdin);
freopen("mentor.out","w",stdout);
#endif
Q=qr();C=qr();
while(Q--){
N=qr();M=qr();S=N+M+1;T=S+1;
Init();
for(int i=1;i<=M;i++)b[i]=qr();
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
x=qr();
if(x)a[i][x].push_back(j+N);
}
}
for(int i=1;i<=N;i++)s[i]=qr();
Solve1();Solve2();
for(int i=1;i<=N;i++)printf("%d ",ans1[i]);
puts("");
for(int i=1;i<=N;i++)printf("%d ",ans2[i]);
puts("");
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
a[i][j].clear();
}
}
}
return 0;
}