github:代码实现之一元线性回归、代码实现之多元线性回归与多项式回归
本文算法均使用python3实现
1. 什么是线性回归
《机器学习》对线性回归的定义为:
给定数据集 $ D = lbrace (x^{(1)}, y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m) } ,y^{(m)}) brace $ ,其中 $ x^{(i)} = lbrace x_1^{(i)},x_2^{(i)},...,x_n^{(i)} brace $ , $ y^{(i)} in R $ ,共有 $ m $ 个样本,每个样本含有 $ n $ 个特征 ,“线性回归”(linear regression)试图学得一个线性模型以尽可能准确地预测实值输出标记。
以一元线性回归为例,我们通过例子来更好地理解什么是线性回归。
现在我们有关于南京夫子庙附近房价的一些数据,$ D =lbrace (x^{(1)}, y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})
brace $ ,其中 $ x^{(i)} $ 只含有一个特征,表示房子的面积 , $ i = 1,2,...,m $ 表示是第 $ i $ 个训练样本 , $ y^{(i)} $ 是数值,表示房子的价格。我们将该数值绘制成下图。

通过观察我们大致可以看出,房子的面积 $ x^{(i)} $ 与房子的价格 $ y^{(i)} $ 具有一定的线性关系,也就是说,我们可以画出能够大致表示 $ x^{(i)} $ 与 $ y^{(i)} $ 关系的一条直线,如下图:

在该直线中,房子的面积 $ x^{(i)} $ 为自变量,房子的价格 $ hat{y}^{(i)} $ 为因变量。而“线性回归”的目的就是,利用自变量 $ x^{(i)} $ 与因变量 $ hat{y}^{(i)}$ ,来学习出这么一条能够描述两者之间关系的线。对于一元线性回归来说就是学习出一条直线,而对于多元线性回归来说则是学习出一个面或超平面。
2. 一元线性回归模型
在概念上理解了线性回归是什么之后,我们就需要将线性回归的问题进行抽象化,转换成我们能够求解的数学问题。
在上面的例子中,我们可以看出自变量 $ x^{(i)} $ 与因变量 $ hat{y}^{(i)} $ 大致成线性关系,因此我们可以对因变量做如下假设(hypothesis):
或者记作:
其中 $ i =1 ,2 ,...,m $
在这里使用 $ hat{y}^{(i)} $ 是由于通过观察,我们可以发现直线并没有完全拟合数据,而是存在一定的误差。该假设即为一元线性函数的模型函数,其中含有两个参数 $ heta_1 与 heta_0 $ 。其中 $ heta_1 $ 可视为斜率, $ heta_0 为则直线在 y $ 轴上的截距。接下来的任务就是如何求得这两个未知参数。
3. 损失函数的定义
通过观察上图,对于 $ x^{(i)} $ 其对应的直线上的值为 $ hat{y}^{(i)} $ ,但所给的数据集中 $ x^{(i)} $ 对应的值为 $ y^{(i)} $ 。而预测值 $ hat{y}^{(i)} $ 与实际值 $ y^{(i)} $ 存在误差(或者也叫做残差(residual),在机器学习中也被称为代价(cost))。我们可以认为,预测值与实际值的误差越小越好。
在这里我们使用均方误差(Mean Squared Error)来描述所需要求解的目标函数(Objective function)或代价函数(Loss function):
其中 $ i = 1,2,..,m $
目标函数 $ J( heta_0, heta_1) $ 描述了所有训练样本实际值与预测值之间的均方误差,而我们的目的就是求解能够使得该误差 $ J( heta_0, heta_1) $ 值最小的参数 $ heta_0, heta_1 $ 。
可将其表示为:
在确定了代价函数以及所需要求解的目标( $ heta_0 , heta_1 $ )以及条件( $ minJ( heta_0, heta_1) $ )之后,接下来需要使用优化算法来进行参数的求解了。
4. 优化算法
在这里我们将使用两种方法进行参数的求解:(1)梯度下降法(2)最小二乘法
我们先观察一下目标函数:
此时将参数 $ heta_1 $ 视作自变量,可将上式看成是 $ J( heta_0, heta_1) $ 是关于 $ heta_1 $ 的二次函数并可作出下图( $ heta_0 $ 亦同)。
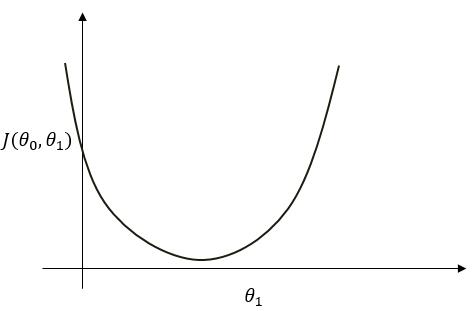
可看出函数图中存在最小点,而在该点处满足 $ frac{Delta J( heta_0, heta_1)}{Delta heta_1} = 0 $。此点即为最小值点。
4.1 梯度下降法(gradient descent)
我们可以使用梯度下降法来求得该点的参数值。其思想为:“走一步看一步”,总是在每一步的小范围内找当前最优方向,再继续前进。
梯度下降法的逻辑为:
(1)从某个 $ heta_0, heta_1 $ 开始(一般设置为0或者取随机值)
(2)不断修改 $ heta_0, heta_1 $ ,以使得 $ J( heta_0, heta_1) $ 越来越小,直到接近最小值点。
其算法过程为:
repeat {
$ heta_j := heta_j - alpha frac{Delta J( heta_0, heta_1)}{Delta heta_j} $
}
其中 $ alpha $ 为学习率(learning rate),也就是每一次的“步长”; $ frac{Delta J( heta_0, heta_1)}{Delta heta_j} $ 是方向,也可以看做是二次函数上每一点的切线斜率,可以使得整体上是朝着最小值点的方向进行。参见下图进行理解:

由上面的梯度下降算法过程可知,我们需要求解学习率 $ alpha $ 以及梯度 $ frac{Delta J( heta_0, heta_1)}{Delta heta_j} ,其中 j = 0,1 $ 。而学习率是人为设定,并不需要从训练集中学习,因此我们只需要求解梯度即可。
对于一元线性回归来说:
则
当 $ j=0 $ 时:
当 $ j=1 $ 时:
于是对于一元线性回归,梯度下降算法过程为:
repeat {
$ heta_0 := heta_0 - alpha frac{1}{m} sum_{i=1}^m (h_{ heta}(x^{(i)}) - y^{(i)}) $
$ heta_1 := heta_1 - alpha frac{1}{m} sum_{i=1}^m (h_{ heta}(x^{(i)}) - y^{(i)}) cdot x^{(i)} $
}
重复以上过程直到收敛,或达到最大迭代次数。
收敛判断条件为:
其中 $ epsilon $ 为阈值 ,当第 $ k $ 次所求代价值,与第 $ k-1 $ 代价值相差小于阈值时,可视为函数收敛到最优解附近。此时的 $ heta_0^{(k)}, heta_1^{(k)} $ 即为所求参数。
以上便是梯度下降算法的整个过程。
4.2 最小二乘法(least square method)
梯度下降是通过迭代的方法求解参数 $ heta $ ,而最小二乘法,或者叫正规方程,是解析地求解参数 $ heta $。下面我们来介绍一下如何使用最小二乘法来求得参数。
对于模型函数,我们可以表示为:
其中
在这里我们对 $ X $ 添加了偏置项 ,$ x_0^{(i)}=1,其中 i = 1,2,...,m $
这是因为 $ h_{ heta}(x^{(i)}) = heta_1 x^{(i)} + heta_0 = heta_1 cdot x_1^{(i)} + heta_0 cdot x_0^{(i)} = heta_1 cdot x_1^{(i)} + heta_0 cdot 1 $ 而 $ x_1^{(i)} $ 为训练样本集中给出的特征。
对于代价函数我们可以表示为:
其中
我们可以把 $ sigma = [X cdot Theta - y]^T[X cdot Theta - y] $ ,因此 $ sigma $ 是关于 $ Theta $ 的二次函数。当 $ frac{Delta sigma}{Delta Theta} = 0 $ 时,$ sigma $ 取得最小值。
因此我们需要直接求解 $ frac{Delta sigma}{Delta Theta} = 0 $ ,即求解 $ frac{Delta}{Delta Theta} [(X cdot Theta - y)^T(X cdot Theta - y)] = 0 $
而
而
而
因此 $ X^T X Theta + X^T X Theta - X^T y - X^T y = 0 $
则 $ 2X^T X Theta = 2 X^T y $ ,由于 $ X^T X $ 是方阵,因此 $ Theta = (X^T X)^{-1} X^T y $
以上便是使用最小二乘法进行参数求解的过程。另外一般来说,矩阵的逆运算算法复杂度为 $ O(n^3) $ ,当特征数很大时,计算非常耗时。
4.3 以上两种方法的比较
梯度下降法:(1)需要选择学习率 $ alpha $ (2)需要迭代 (3)即使特征数 $ n $ 很大也能很好地工作。
最小二乘法:(1)不需要选择学习率 $ alpha $ (2)不需要迭代 (3)需要计算矩阵的逆,当特征数 $ n $ 很大时,计算速度很慢。
5. 多元线性回归
5.1 多元线性回归模型
对于多元线性回归模型,对训练样本集拟合时不再是一条“直线”,而是“面”或者“超平面”。
拟合的方程为:
其中 $ i = 1,2,...,m $ 表示第 $ i $ 个训练样本。
或者记为:
其中 $ m $ 表示训练样本数, $ n $ 表示特征数。
在此我们同样添加了偏置项 $ x_0^{(i)} = 1 $ 相关解释不再赘述。
5.2 损失函数定义
对于多元线性回归模型,其损失函数定义为:
其中
5.3 优化算法--梯度下降法
其算法过程为:
repeat {
$ heta_j := heta_j - alpha frac{1}{m} sum_{i=1}^m (h_{ heta}(x^{(i)}) - y^{(i)}) cdot x_j^{(i)} $
}
其中 $ i = 1,2,...,m,表示样本数 ; j = 1,2,..,n,表示特征数 $
梯度的计算过程同一元线性回归中的梯度求解过程。
引用及参考:
[1]《机器学习》周志华著
[2] https://blog.csdn.net/perfect_accepted/article/details/78383434
写在最后:本文参考以上资料进行整合与总结,属于原创,文章中可能出现理解不当的地方,若有所见解或异议可在下方评论,谢谢!
若需转载请注明:https://www.cnblogs.com/lliuye/p/9120839.html