假设我们要求解以下的最小化问题: $min_xf(x)$
如果$f(x)$可导,那么一个简单的方法是使用Gradient Descent (GD)方法,也即使用以下的式子进行迭代求解:
$x_{k+1} = x_k - aDelta f(x_k)$
如果$Delta f(x)$满足L-Lipschitz,即:
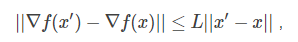
那么我们可以在点$x_k$附近把$f(x)$近似为:

把上面式子中各项重新排列下,可以得到:
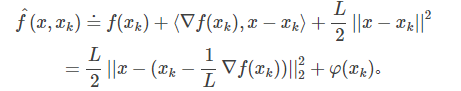
这里$varphi (x_k)$不依赖于x,因此可以忽略。
显然,$hat f(x, x_k)$的最小值在
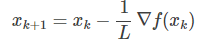 获得。所以,从这个角度看的话,GD的每次迭代是在最小化原目标函数的一个二次近似函数.(梯度下降的由来的推导,这里说的不好,参考这里: http://www.cnblogs.com/ljygoodgoodstudydaydayup/p/7274943.html)
获得。所以,从这个角度看的话,GD的每次迭代是在最小化原目标函数的一个二次近似函数.(梯度下降的由来的推导,这里说的不好,参考这里: http://www.cnblogs.com/ljygoodgoodstudydaydayup/p/7274943.html)
在很多最小化问题中,我们往往会加入非光滑的惩罚项$g(x)$, 比如常见的L1惩罚: $g(x) = ||x||_1$ .这个时候,GD就不好直接推广了。但上面的二次近似思想却可以推广到这种情况:
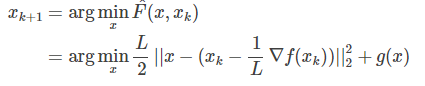
这就是所谓的Proximal Gradient Descent (PGD)算法,即目标函数由损失项和正则项组成。对于上式,可先计算$z = x_k - frac{1}{L}Delta f(x_k)$, 然后求解
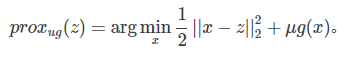

软阈值(SoftThresholding)可以求解如下优化问题:
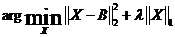
其中:
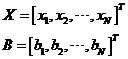
根据范数的定义,可以将上面优化问题的目标函数拆开:
也就是说,我们可以通过求解N个独立的形如函数
的优化问题,来求解这个问题。由中学时代学过的求极值方法知道,可以求函数f(x)导数:
令函数f(x)导数等于0,得:
这个结果等号两端都有变量x,需要再化简一下。下面分三种情况讨论:
(1)当b>λ/2时
假设x<0,则sgn(x)=-1,所以x=b+λ/2>0,与假设x<0矛盾;(λ > 0)
假设x>0,则sgn(x)=1,所以x=b-λ/2>0,成立;
所以此时在x=b-λ/2>0处取得极小值:

即此时极小值小于f(0),而当x<0时
即当x<0时函数f(x)为单调降函数(对任意△x<0,f(0)<f(△x))。因此,函数在x=b-λ/2>0处取得最小值。
(2)当b<-λ/2时
假设x<0,则sgn(x)=-1,所以x=b+λ/2<0,成立;
假设x>0,则sgn(x)=1,所以x=b-λ/2<0,与假设x>0矛盾;
所以此时在x=b+λ/2<0处取得极小值:
即此时极小值小于f(0),而当x>0时
即当x>0时函数f(x)为单调升函数(对任意△x>0,f(△x)>f(0))。因此,函数在x=b+λ/2<0处取得最小值。
(3)当-λ/2<b<λ/2时(即|b|<λ/2时)
假设x<0,则sgn(x)=-1,所以x=b+λ/2>0,与假设x<0矛盾;
假设x>0,则sgn(x)=1,所以x=b-λ/2<0,与假设x<0矛盾;
即无论x为大于0还是小于0均没有极值点,那么x=0是否为函数f(x)的极值点呢?
对于△x≠0,
当△x >0时,利用条件b<λ/2可得
当△x <0时,利用条件b<λ/2可得(注:此时|△x |=-△x)
因此,函数在x=0处取得极小值,也是最小值。
综合以上三种情况,f(x)的最小值在以下位置取得:
至此,我们可以得到优化问题
的解为
http://blog.csdn.net/bingecuilab/article/details/50628634
http://blog.csdn.net/jbb0523/article/details/52103257












