LGP5490
题意
给定若干组((x_1,y_1,x_2,y_2)),求所有这样的两点构成的平行于坐标轴矩形的面积之并。
面积并
面积的求法:(sumlimits)截线段长度( imes)扫过的高度

考虑这个图像,如何模拟扫描线从下向上扫过图形,并且快速计算出当前扫描线被截的长度。
现在假设,扫描线每次会在碰到横边时停下来。如图。

简单来说,可以对图形面积产生影响的元素,也就是这些横边左右端点的坐标。
为了快速计算出截线段长度,可以将横边赋值不同的权值。具体为:对于一个矩形,其下边权值为1,下边权值为(-1)。
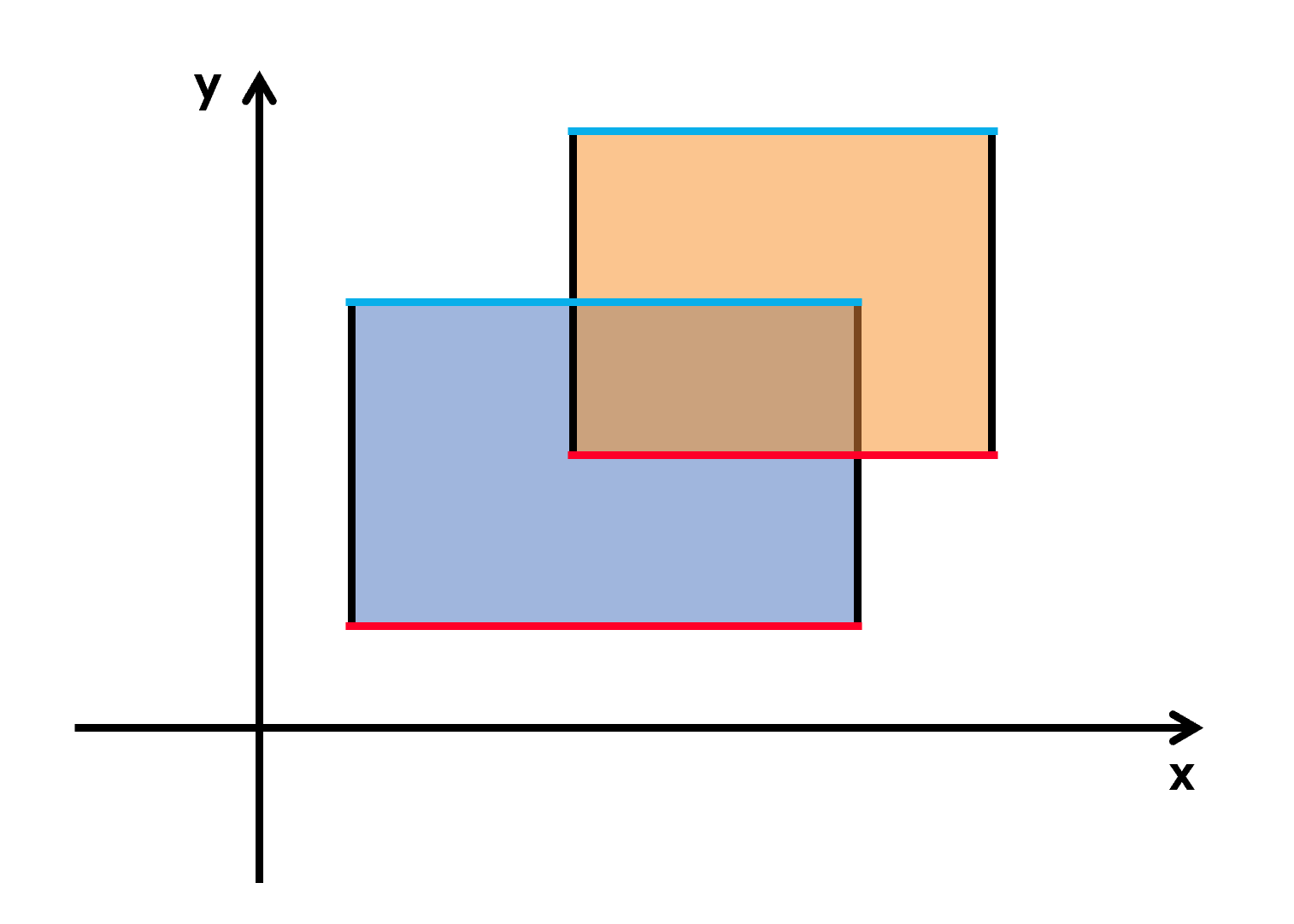
然后把所有横边按照(y)坐标升序排序。这样,对于每一个矩形,扫描线总是会先碰到下边,再碰到上边。这样可以保证扫描线所截的长度为非负。
这样操作以后,可以使用线段树。先把所有端点在(x)轴上离散化。

在上面的例子中,(4)个端点的纵投影总共把(x)轴切割成了5部分。取中间的三部分线段,建立一颗线段树,每一个端点维护一条线段【也就是一个区间】的信息:
- 该线段被覆盖了多少次(被多少个矩形所覆盖)
- 该线段内被整个图形所截的长度是多少。

只要一条线段被覆盖,那么它一定被图形所截。这样转化为了一个区间查询问题,即:每次将当前扫描线扫到的边对应的信息按照之前赋值的权值更新,再查询线段树根节点的信息,得到当前扫描线扫过的面积。
模拟过程:
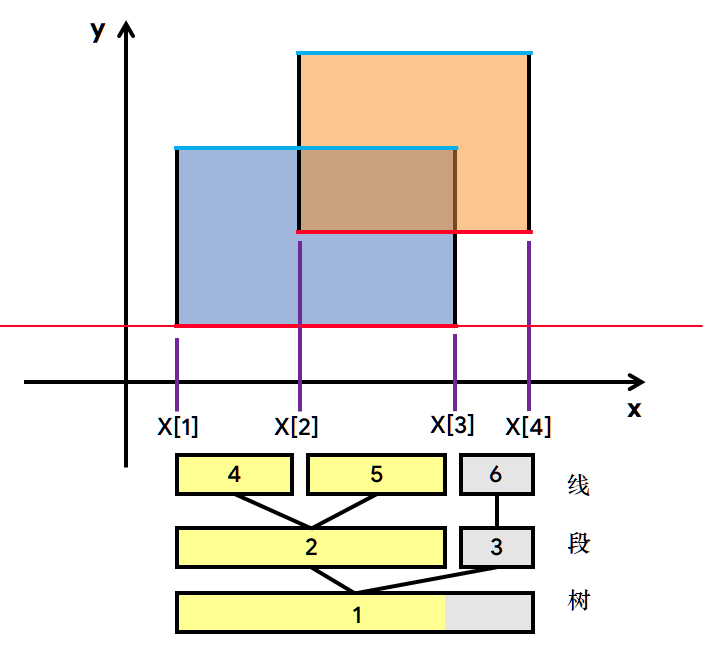
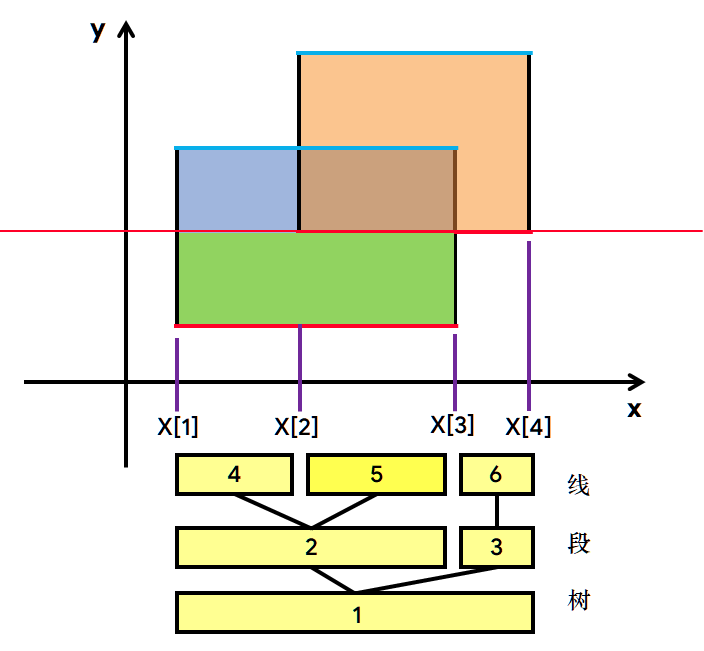
上图的5号节点(sum=2),绿色表示已经计算的面积。

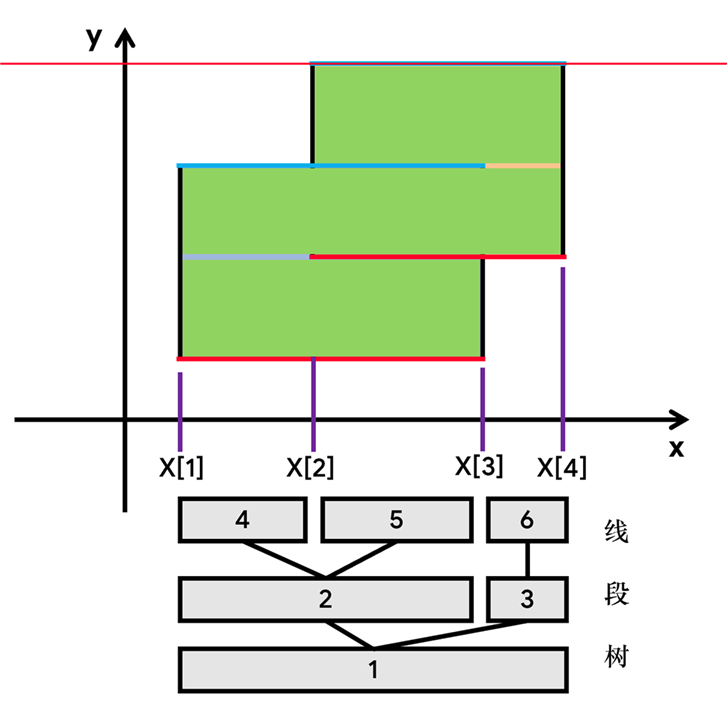
线段树怎么建?
建树
void build_tree(int x, int l, int r) {
// 初始化节点信息
if(l == r)
return;
int mid = (l + r) >> 1;
build_tree(lson, l, mid);
build_tree(rson, mid + 1, r);
return;
}
这棵线段树的每个节点都对应了一条线段。考虑将线段树上节点对应的区间和横边建立映射。
对于一个叶子节点(x),建树时已经保证(tree_x.l=tree_x.r),但是他保存的信息显然不是某条线段的一个端点。(如果一条线段的两个端点重合,本质上仅是一个点)。再看一个节点的左右儿子,同样的,建树的时候已经保证了左右儿子的区间不会重合(交集为空),但看这样两条相邻线段:([1,2],[2,3]),你会发现([1,2]∩[2,3]={2}),也就是左儿子的右端点和右儿子的左端点其实是重合的。
考虑把线段树每个节点(x)对应的区间((tree_x.l,tree_x.r))不变,改变区间和横边的映射关系,具体为:节点(x)对应([X[tree_x.l],X[tree_x.r+1]])这条横边。这里将右端点的对应关系更改了。
code
#include <cstdio>
//不开cmath,y1有定义
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn=1e6+10;
int n,cnt=0;
long long x1,y1,x2,y2,X[maxn<<1];
struct scanline{
long long l,r,h;
int mark;//保存权值(1/-1)
bool operator <(const scanline &rhs) const{
return h<rhs.h;
}
}line[maxn<<1];
struct segtree{
int l,r,sum;
long long len;
//sum:被完全覆盖的次数
//len:区间内被截的长度
}tree[maxn<<2];
void buildtree(int x,int l,int r){
tree[x].l=l,tree[x].r=r;
tree[x].len=0;
tree[x].sum=0;
if(l==r) return ;
int mid=(l+r)>>1;
buildtree(x<<1,l,mid);
buildtree(x<<1|1,mid+1,r);
return ;
}
void pushup(int x){
int l=tree[x].l,r=tree[x].r;
if(tree[x].sum)//被覆盖过
tree[x].len=X[r+1]-X[l];//更新长度
else
tree[x].len=tree[x<<1].len+tree[x<<1|1].len;//合并儿子信息
}
void edittree(int x,long long L,long long R,int c){
int l=tree[x].l,r=tree[x].r;
//这里的l,r和L,R意义不同,l,r表示这个节点管辖的下标范围,而L,R表示要修改的区间
if(X[r+1]<=L||R<=X[l]) return ;
//这里加等号的原因:假设现在考虑[2,5][5,8]两条线段,希望修改[1,5]区间的sum
//虽然5在这个区间内,但是[5,8]并不是我们想要修改的线段,所以加上了等号
if(L<=X[l]&&X[r+1]<=R){
tree[x].sum+=c;
pushup(x);
return ;
}
edittree(x<<1,L,R,c);
edittree(x<<1|1,L,R,c);
pushup(x);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld%lld",&x1,&y1,&x2,&y2);
X[2*i-1]=x1,X[2*i]=x2;
line[2*i-1]=(scanline){x1,x2,y1,1};
line[2*i]=(scanline){x1,x2,y2,-1};
//线段含两个端点,一个矩形的上下边都需要扫过
}
n<<=1;
sort(line+1,line+n+1);
sort(X+1,X+n+1);
int tot=unique(X+1,X+n+1)-X-1;//去重
buildtree(1,1,tot-1);
//tot-1的原因:因为右端点的对应关系已经被修改了,[1,tot-1]其实就是[X[1],X[tot]]
long long ans=0;
for(int i=1;i<n;i++){//最后一条边不管
edittree(1,line[i].l,line[i].r,line[i].mark);
ans+=tree[1].len*(line[i+1].h-line[i].h);
}
printf("%lld",ans);
return 0;
}