P1990 覆盖墙壁题解

题目传送门

用如下两种砖块（可旋转）填充 (2 imes n) 的墙壁，求出不重复方案数，结果对 (10^4) 取模。

按照惯例，定义 (F_n)为填满(2 imes n) 墙壁的方案总数，边界条件 (F_0 = 1)，对于 (k<0)，(F_k=0)。（(F_0)表示无需再填，(F_k(k<0)) 表示无意义情况）

考虑最后放的情况：
1、放 (1) 个 (2 imes 1)的砖块（竖放）：显然它的方案数为 (F_{n-1});(图1)

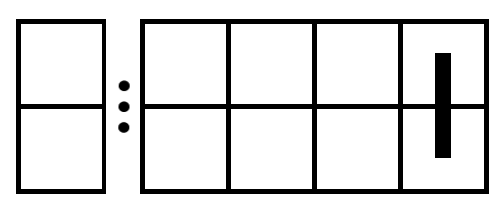
2、放 (2) 个 (2 imes 1)的砖块（横放）：方案数为 (F_{n-2})；（图 2）

3、放 (1) 个 (L) 型砖块（因为该砖块可以翻转着放，所以这样放的总方案数要乘 (2)）：这么填会带来 (1) 个格子的突出，如何消去这个突出？
（1）、再放 (1) 个 (L) 型砖块，恰好消去突出，方案数 (F_{n-3})；（图 3-1）

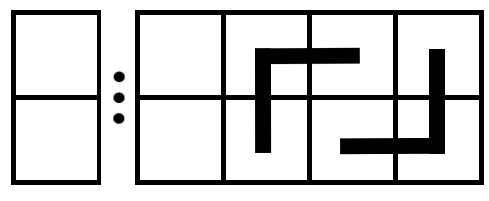
（2）、横放 (1) 个 (2 imes 1) 的砖块，再放 (L) 型砖块，方案数 (F_{n-4})（图 3-2）；

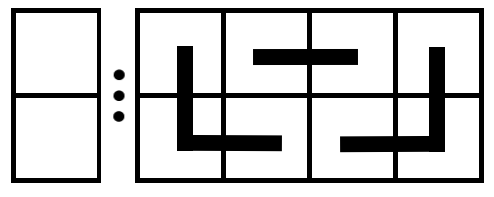
（3）、(2 imes 1) 的砖块可以交替着放下去，再补上一个 (L) 型砖块，从而消去这个突出。直到 (2 imes 1) 砖块和 (L) 型砖块恰好填满墙壁（(F_0)）。

综上，最后放 (1) 个 (L) 型砖块得到的方案数为 (2 imes (F_{n-3}+F_{n-4}+...+F_{0}))（已经乘了 (2)）。

综合 (3) 种情况，得：

$F_n=F_{n-1}+F_{n-2}+2cdot (F_{n-3}+F_{n-4}+...+F_0)=sumlimits_{i=0}^{n-1}F_i + sumlimits_{i=0}^{n-3}F_i$

我们为了找出递推式，其实就是想找出(F_n)与(F_{n-1})或者(F_{n-2})或者(F_{n-3})的关系，所以：
令(n=k)，得
(F_k=sumlimits_{i=0}^{k-1}F_i + sumlimits_{i=0}^{k-3}F_i=F_{k-1}+F_{k-2}+ 2cdot F_{k-3}+2cdot sumlimits_{i=0}^{k-4}F_i)

令(n=k-1),得
(F_{k-1}=sumlimits_{i=0}^{k-2}F_i + sumlimits_{i=0}^{k-4}F_i=F_{k-2}+F_{k-3}+2cdot sumlimits_{i=0}^{k-4}F_i)

上式减去下式得：
(F_k-F_{k-1}=F_{k-1}+F_{k-3})
移项就得到(F_k=2cdot F_{k-1}+F_{k-3})

于是这个递推式就得到的化简:
(F_n=sumlimits_{i=0}^{n-1}F_i+sumlimits_{i=0}^{n-3}F_i=2 cdot F_{n-1}+F_{n-3})

C++代码

#include<bits/stdc++.h>

using namespace std;
const int N = 1000010;
int f[N], n;
const int MOD = 10000;

int main() {
    //手工计算出前三个初始值
    f[0] = 1;
    f[1] = 1;
    f[2] = 2;
    cin >> n;
    for (int i = 3; i <= n; i++) {
        //每一步都要取模
        f[i] = (f[i - 1] * 2) % MOD + f[i - 3] % MOD;
        f[i] %= MOD;
    }
    printf("%d
", f[n]);
    return 0;
}