大致总结一下学到的各个优化算法。
一、梯度下降法
函数的梯度表示了函数值增长速度最快的方向,那么与其相反的方向,就可看作函数减少速度最快的方向。
在深度学习中,当目标设定为求解目标函数的最小值时,只要朝梯度下降的方向前进,就可以不断逼近最优值。
梯度下降主要组成部分:
1、待优化函数f(x)
2、待优化函数的导数g(x)
3、变量x,用于保存优化过程中的参数值
4、变量x点处的梯度值:grad
5、变量step,沿梯度下降方向前进的步长,即学习率
假设优化目标函数为:f(x) = (x-1)^2,那么导数为f'(x) = g(x) = 2x - 2。我们可以直接看出最优值在x = 1处取得。
import numpy as np import matplotlib.pyplot as plt def f(x): return (x-1)**2 def g(x): return 2 * x -2 def gd(x_start, step, g): x_list = [] y_list = [] x = x_start for i in range(20): grad = g(x) x = x - step*grad #往梯度反方向更新,***重点*** x_list.append(x) y_list.append(f(x)) print('x = {:}. grad = {:}, y = {:}'.format(x, grad, f(x))) if grad < 1e-6: break; return x_list,y_list x = np.linspace(-8,10,200) y = f(x) //初始点为 x = 10, step = 0.1 x_gd, y_gd = gd(10, 0.1, g) plt.plot(x, y) plt.plot(x_gd, y_gd, 'r.') plt.savefig('gradient_descent.png') plt.show()
输出结果:
x = 8.2. grad = 18, y = 51.83999999999999 x = 6.76. grad = 14.399999999999999, y = 33.1776 x = 5.608. grad = 11.52, y = 21.233663999999997 x = 4.6864. grad = 9.216, y = 13.58954496 x = 3.9491199999999997. grad = 7.3728, y = 8.697308774399998 x = 3.3592959999999996. grad = 5.8982399999999995, y = 5.5662776156159985 x = 2.8874367999999997. grad = 4.718591999999999, y = 3.562417673994239 x = 2.5099494399999998. grad = 3.7748735999999994, y = 2.2799473113563127 x = 2.2079595519999997. grad = 3.0198988799999995, y = 1.45916627926804 x = 1.9663676415999998. grad = 2.4159191039999994, y = 0.9338664187315456 x = 1.7730941132799998. grad = 1.9327352831999995, y = 0.5976745079881891 x = 1.6184752906239999. grad = 1.5461882265599995, y = 0.3825116851124411 x = 1.4947802324992. grad = 1.2369505812479997, y = 0.2448074784719623 x = 1.3958241859993599. grad = 0.9895604649983998, y = 0.15667678622205583 x = 1.316659348799488. grad = 0.7916483719987197, y = 0.10027314318211579 x = 1.2533274790395903. grad = 0.633318697598976, y = 0.06417481163655406 x = 1.2026619832316723. grad = 0.5066549580791806, y = 0.04107187944739462 x = 1.1621295865853378. grad = 0.40532396646334456, y = 0.026286002846332555 x = 1.1297036692682703. grad = 0.32425917317067565, y = 0.016823041821652836 x = 1.1037629354146161. grad = 0.2594073385365405, y = 0.010766746765857796

二、Momentum动量算法
其实本质和梯度下降差不多,只是在更新梯度时,在原有梯度下降法的基础上,会将上一次的梯度乘上一个衰减率(pre_grad * discount),加入到本次的梯度更新中。
那么动量算法对比梯度下降法的好处在哪里呢?我们假设优化目标函数:z=x^2 + 50*y^2,那么使用梯度下降法的效果如何?请看:
import numpy as np import matplotlib.pyplot as plt def f(x): return x[0]*x[0] + 50*x[1]*x[1] def g(x): return np.array([2*x[0], 100 * x[1]]) def gd(x_start, step, g): x_list = [] y_list = [] x = x_start x_list.append(x[0]) y_list.append(x[1]) for i in range(50): grad = g(x) x = x - step * grad print('ljj=',x) x_list.append(x[0]) y_list.append(x[1]) print('x = {:}. grad = {:}, y = {:}'.format(x, grad, f(x))) if grad.all() < 1e-6: break; return x_list, y_list def momentum(x_start, step, g, discount = 0.7): x_list = [] y_list = [] x = x_start x_list.append(x[0]) y_list.append(x[1]) pre_grad = np.zeros_like(x) for i in range(50): grad = g(x) pre_grad = pre_grad * discount + step * grad #将上一次更新量的乘上discount,再加上当前的梯度更新量。将结果用作本次更新 x = x - pre_grad print('ljj=',x) x_list.append(x[0]) y_list.append(x[1]) print('x = {:}. grad = {:}, y = {:}'.format(x, grad, f(x))) if grad.all() < 1e-6: break; return x_list, y_list xi = np.linspace(-200,200,1000) yi = np.linspace(-100,100,1000) X, Y = np.meshgrid(xi, yi) Z = X*X + 50*Y*Y #Gradient Descent #xx,ss = gd([150, 75], 0.016, g) #xx,ss = gd([150, 75], 0.019, g) #Momentum xx,ss = momentum([150, 75], 0.019, g) print('xx=',xx) print('xx=',xx[0]) plt.contour(X, Y, Z) plt.plot(0,0, 'r*') plt.plot(xx,ss) plt.show()
梯度下降法【step = 0.016,迭代50次】:
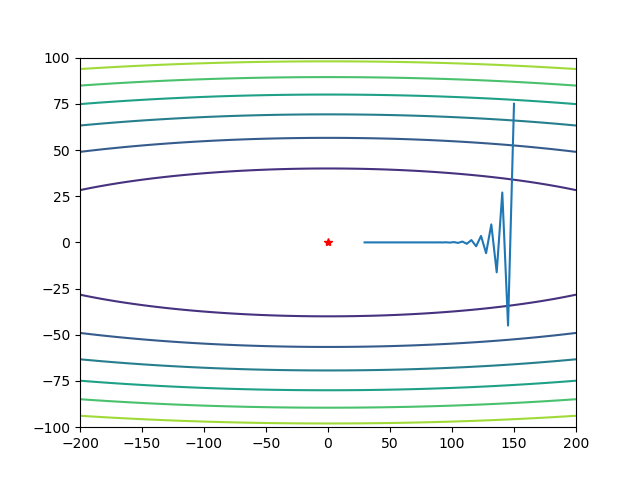
梯度下降法【step = 0.019,迭代50次】:

动量算法【step = 0.019,迭代50次】:

从优化的路径来看,
梯度下降法,确实能够不断逼近最优值,但是由于存在冗余的Y方向上的更新,从而导致震荡明显,这些震荡有一部分是多余的开销。并且需要迭代次数较多,才能接近最优值。
动量算法,能够有效较少震荡,同时,加速优化,迭代次数相比梯度下降法更少,更快地逼近最优值。
三、Nesterov算法
在动量算法的基础上,再更进一步,计算梯度。--------简单来说,与动量算法的本质区别,只是在于计算梯度的区别:
1、动量算法:在当前目标点,计算梯度。
2、Nesterov:在当前目标的点基础上,再使用上次的梯度,进行一次动量更新,从而达到更新后的优化点。然后在此点上计算梯度。
def nesterov(x_start, step, g, discount = 0.7): x_list = [] y_list = [] x = x_start x_list.append(x[0]) y_list.append(x[1]) pre_grad = np.zeros_like(x) for i in range(50): x_future = x - pre_grad*step*discount #使用上次的梯度,进行一次动量更新 grad = g(x_future) #在更新后的优化点上,计算梯度 pre_grad = pre_grad * discount + grad x = x - pre_grad *step print('ljj=',x) x_list.append(x[0]) y_list.append(x[1]) print('x = {:}. grad = {:}, y = {:}'.format(x, grad, f(x))) if grad.all() < 1e-6: break; return x_list, y_list xx,ss = nesterov([150, 75], 0.012, g)
结果如下:

通过调参(discount,step)可以看到,优化过程中,y轴方向的震荡明显快速减小。这就是Nesterov的效果。