协方差是统计学上表示两个随机变量之间的相关性,随机变量ξ的离差与随机变量η的离差的乘积的数学期望叫做随机变量ξ与η的协方差(也叫相关矩),记作cov(ξ, η):
cov(ξ, η) = E[(ξ-Eξ)(η-Eη)] = E(ξη)-EξEη
对于离散随机变量,我们有:

对于连续随机变量,我们有:

随机变量的协方差用来描述随机变量之间的相关性,如果ξ与η独立,则cov(ξ, η)=0. 如果ξ与η相同,则cov(ξ, η)就是变量ξ的方差.
协方差矩阵是一个矩阵,其每个元素是各个矢量元素之间的协方差。这是从标量随机变量到高维度随机矢量的自然推广.
假设 是以
是以 个标量随机变量组成的列矢量,
个标量随机变量组成的列矢量,
并且 是其第i个元素的期望值,即,
是其第i个元素的期望值,即, 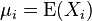 。协方差矩阵被定义的第i,j项是如下:
。协方差矩阵被定义的第i,j项是如下:
即:
矩阵中的第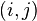 个元素是
个元素是 与
与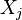 的协方差。这个概念是对于标量随机变量方差的一般化推广。
的协方差。这个概念是对于标量随机变量方差的一般化推广。
进一步的分析协方差矩阵

∂i 表示各样本的Xi变量不同样本值组成的向量(i=1,2,...n);
βj 表示某一个样本 j 的各变量值组成的向量(j=1,2,...,m);
用 μi 表示Xi的期望,即 μi =E(Xi).


协方差矩阵为

如果所有μi =E(Xi)=0.则上面表达式就变为:

(实际计算中,分母是m-1,而不用m)
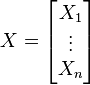
![\Sigma=\mathrm{E}
\left[
\left(
\textbf{X} - \mathrm{E}[\textbf{X}]
\right)
\left(
\textbf{X} - \mathrm{E}[\textbf{X}]
\right)^\top
\right]](http://upload.wikimedia.org/math/1/8/1/1811f942680a72974597be42c28d31d2.png)
![=
\begin{bmatrix}
\mathrm{E}[(X_1 - \mu_1)(X_1 - \mu_1)] & \mathrm{E}[(X_1 - \mu_1)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_1 - \mu_1)(X_n - \mu_n)] \\ \\
\mathrm{E}[(X_2 - \mu_2)(X_1 - \mu_1)] & \mathrm{E}[(X_2 - \mu_2)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_2 - \mu_2)(X_n - \mu_n)] \\ \\
\vdots & \vdots & \ddots & \vdots \\ \\
\mathrm{E}[(X_n - \mu_n)(X_1 - \mu_1)] & \mathrm{E}[(X_n - \mu_n)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_n - \mu_n)(X_n - \mu_n)]
\end{bmatrix}](http://upload.wikimedia.org/math/a/1/2/a12a573ecd1d853abd8c01fab9fccfbe.png)