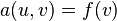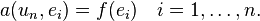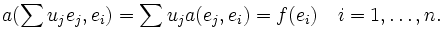伽辽金法

原文链接

伽辽金方法（Galerkin method）是由俄罗斯数学家鲍里斯·格里戈里耶维奇·伽辽金（俄文：Борис Григорьевич Галёркин 英文：Boris Galerkin）发明的一种数值分析方法。应用这种方法可以将求解微分方程问题（通过方程所对应泛函的变分原理）简化成为线性方程组的求解问题。而一个高维（多变量）的线性方程组又可以通过线性代数方法简化，从而达到求解微分方程的目的。

伽辽金法采用微分方程对应的弱形式，其原理为通过选取有限多项试函数（又称基函数或形函数），将它们叠加，再要求结果在求解域内及边界上的加权积分（权函数为试函数本身）满足原方程，便可以得到一组易于求解的线性代数方程，且自然边界条件能够自动满足。

必须强调指出的是，作为加权余量法的一种试函数选取形式，伽辽金法所得到的只是在原求解域内的一个近似解（仅仅是加权平均满足原方程，并非在每个点上都满足）。

因为伽辽金方法的妙处在于研究它们的抽象方法，所以我们首先给出它们的抽象推导。最后我们再给出应用的例子。

一个问题的弱形式

我们通过一个抽象问题来引入伽辽金方法，将问题表示成在一个希尔伯特空间上的弱形式，也就是，求解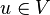使得对于所有

成立。这里，是一个双线性型表达式，是一个上的线性形表达式。

伽辽金离散化

选取一个n 维子空间，然后求解问题在子空间中的投影：求使得对于所有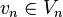

我们称这个方程为伽辽金方程。注意方程形式没有改变，但是求解域改变了。

伽辽金正交性

这是使得伽辽金方法非常有效的关键性质。因为，我们可以取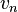为原方程的一个试矢量。带入并相减，便得到误差的伽辽金正交性关系

这里是真实解和伽辽金方程的解之间的误差。

矩阵形式

因为伽辽金方法的目标是将问题简化为线性方程组，我们来构造它的矩阵形式，以便利用计算机进行数值求解。

令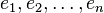为空间中的一组基。则显然依次选取这些基矢量作为伽辽金方程的试矢量是充分的，也即：求解使得

用上述基矢量表示出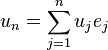：，将其代入上面的方程得到

这样我们就得到了上面这组型的线性方程组，式中

矩阵的对称性

由于矩阵项的定义，伽辽金方程的系数矩阵是对称矩阵的充要条件是双线性型表达式是对称的。