写在前面的话:感谢liouzhou_101(亲爱的大宝贝)在解题和总结的过程提供的若干建议和帮助。
进入正题:
题目来源:csacademy
Time limit: 1500 ms
Memory limit: 128 MB
题目描述:
一条很宽的河面上有n个高度不同柱子,它们排列成一条直线直到河的对岸。我们想要使用这些柱子作为支撑来建造一座桥。为了实现这个目标,我们将选取这些柱子的子集,并将他们的顶端连接起来作为桥的一部分,我们必须选取第一和最后一个柱子。
在连接两个柱子i,j的花费为(hi−hj)2,hi是i柱子的高度,不在桥范围内的柱子我们将移除掉,移除柱子i所需的花费为wi,wi可以为负数。
现在我们需要求建造这座桥的最小花费,包括连接相邻的柱子和移除不需要的柱子的开销。
Input:
第一行输入一个整数n,代表有n个柱子。第二行有n个整数,是h[i]。第三行也有n个整数,是为w[i]。
数据范围:
2<=n<=105
0<=hi<=106
0<=|wi|<=106
Output:输出一个数,表示建造这座桥最小花费。
Subtask 1 (30 points)
n≤1000
Subtask 2 (30 points)
optimal solution includes at most 2 additional pillars (besides the first and last)
Subtask 3 (40 points)
no additional constraints
解析——子任务一:
通过观察题目发现,是有子任务的。我们可以考虑小数据的子任务,即n=1000的情况。这时候,我们可以采取线性规划的办法,令f[i]为算法运行到第i个柱子并且选中第i个柱子时的最小花费。
其动态规划方程是为:f[i] = min{(h[i]-h[j])2 + + f[j]}其中j∈[1,i-1],其含义是当我选中第i个柱子的时候,寻找在它前面与其相邻的j柱子,此时花费是最小。对于每个柱子i求得其相应的f[i],则最后答案是f[n]。
而该规划方程中的 ,则可以对w[]序列求出前缀和s[],此项就可以用s[i-1]-s[j]求得,并不用每次都进行求和。如此这般,我们就解决了子任务一。
code:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
#include <cstring>
#include <queue>
#include <ctime>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const ll INF = 1ll<<50;
const int maxN = 100010;
const int maxF = 1000000010;
int h[maxN];
int w[maxN];
ll f[maxN];
ll a[maxN];
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&h[i]);
for(int i=1;i<=n;i++)
{
scanf("%d",&w[i]);
s[i] = s[i-1]+w[i];
}
for(int i=2;i<=n;i++)
{
ll minn = INF;
for(int j=1;j<i;j++)
{
ll tmp = (ll)(h[i]-h[j]) * (ll)(h[i]-h[j]) + (s[i-1] - s[j]) + f[j];
if(tmp < minn)
minn = tmp;
}
f[i] = minn;
}
printf("%lld ",f[n]);
return 0;
}
解析:100分解法
现在考虑原始数据的情况,当n = 10^5的时候,使用动态规划分方法已经不能满足题目复杂度的需求了,我们需要基于之前的动态规划方程,进行算法的优化。
f[i] = min{(h[i] – h[j])^2 + s[i-1] – s[j] + f[j]}这是之前的动态规划方程。对大括号内的东西进行变形:
(h[i] – h[j])^2 + s[i-1] – s[j] + f[j]
= h[i]^2 + h[j]^2 – 2*h[i]h[j]+s[i-1] – s[j] + f[j]
= f[j]-s[j]+h[j]^2 – 2*h[i]h[j] + h[i]^2 + s[i-1]
令Y[j] = f[j]-s[j]+h[j]^2;x[j]= 2*h[j],G[i]= h[i]^2 + s[i-1].则之前的动态规划方程可以变形为F[i] = min {Y[j]-h[i]X[j]} + G[i]。因为对于确定的i来说,h[i]和G[i]都是确定的,需要最小化的是Y[j] – h[i]X[j]。令z = Y[j] – h[i]X[j],Y = hX + z.现在问题转换为对于i前面的所有j所对应的(X[j],Y[j])点对,找到一点,在给定斜率h[i]的情况下,使得z最小。如下图示意,红线在y轴截距z是最小的。
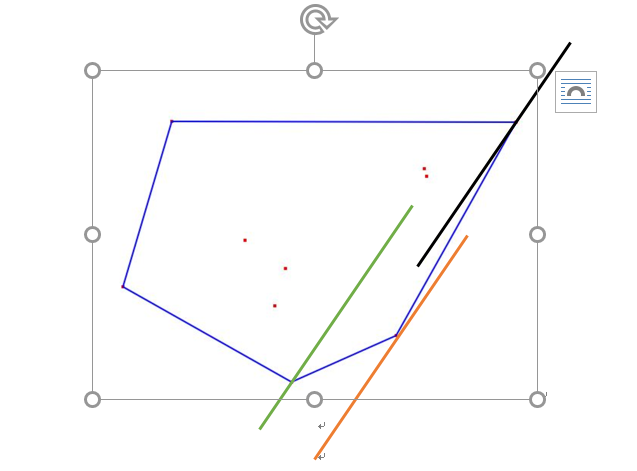
明显的上图多边形形状是为凸包,更为明显的是,只有右下部分是有用的,也就是下凸壳。对于下凸壳来说,我们定义某个点的斜率为该点和右边最邻近点形成线段的斜率,而满足组成下凸壳的点的集合的要求为:斜率k[x]是递增的,最末尾的点斜率定义为无穷。
我们在程序中主要的两个操作是:1)维护一个下凸壳;2)对给定斜率h[i],在下凸壳中找到一个点,使得在通过此点的斜率为h[i]的直线在Y截距z是为最小。而该点的斜率为lower_bound(h[i])。
维护下凸壳使用的数据结构为平衡树,直接使用stl中的set模板类即可。维护凸壳的操作大致分为两种:1)按照位置插入点;2)对给定斜率h[i],找到大于等于它的最小值。则对平衡树中的点有两种比较大小的模式,而这里并不需要两颗平衡树,只需要一个变量flag表示不同比较大小的方式。具体实现如下:对于平衡树中的节点,在不同情况下对小于号的进行不同的重载。
struct node{
ll x,y;
ld k;
bool operator < (const node &n)const
{
if(flag == 0)
return(x < n.x || x == n.x && y<n.y); //按位置次序插入
else
return ( k < n.k); //按斜率寻找
}
};
解决完平衡树中对小于号的不同重载,我们将考虑到插入某个点之后,将会对整个凸壳的形状产生影响,我们需要对这个凸壳进行检查,删掉那些破坏凸壳的点。我们按以下步骤对插入某点后对凸壳进行检查。设某点插入到平衡树中的位置为it.
第一步:检查it与x=it++,y=it--,这三点是否满足成为凸壳的一部分。是否满足这里,需要有个函数det()判断线段(y,it),(it,x)向量积是否大于0,若大于,则满足,反之则不满足。如果插入位置与其上下相邻两点满足凸壳,则继续下一步分检查;如果插入该点不满足,则将该点删掉,而之前的凸壳没有发生任何变化,无需进行检查,对下一个柱子进行分析。
第二步:从当前位置向后检查,删除掉不在凸壳上的点。
第三步:从当前位置向前检查,删除掉不在凸壳上的点。
检查完毕之后,现有的点仍然组成一个凸壳,并更新it位置,和it之前位置的斜率。凸壳最后一个点的斜率设为无穷。
对于每个柱子i,就可以找到最佳的j柱子所对应在凸壳上的点,继而计算出f[i],并将柱子i对应的X[i],Y[i]计算出来,插入到平衡树中,维护凸壳,如此不断计算,最后的答案是f[n]。
Code:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
#include <cstring>
#include <queue>
#include <ctime>
#include <set>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int,int> pii;
const ll INF = 1ll<<50;
const int maxN = 1000010;
const int maxF = 1000000010;
ll h[maxN];
ll w[maxN];
ll s[maxN];
ll f[maxN];
int flag;
struct node{
ll x,y;
ld k;
bool operator < (const node &n)const
{
if(flag == 0)
return(x < n.x || x == n.x && y<n.y); //按位置次序插入
else
return ( k < n.k); //按斜率寻找
}
};
set<node> H;
ll getY (int j)
{
return (f[j] - s[j] + h[j]*h[j]);
}
ll getX (int j)
{
return (2*h[j]);
}
ll getG(int i)
{
return (s[i-1] + h[i]*h[i]);
}
ll det(set<node>::iterator a,set<node>::iterator b,set<node>::iterator c)
{
ll cnt = (a->x * b->y - a->y*b->x) + (b->x * c->y - c->x*b->y)+(a->y * c->x - a->x * c->y);
return cnt;
}
int main()
{
freopen("a.txt","r",stdin);
freopen("b.txt","w",stdout);
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lld",&h[i]);
for(int i=1;i<=n;i++)
{
scanf("%lld",&w[i]);
}
for(int i=1;i<=n;i++)
{
s[i] = s[i-1]+w[i];
}
node tmp;
flag = 0;
tmp.x = getX(1);
tmp.y = getY(1);
tmp.k = 1e100;
H.insert(tmp);
for(int i=2;i<=n;i++)
{
flag = 1;
tmp.k = h[i]; //相当于斜率
set<node>::iterator it = H.lower_bound(tmp);
f[i] = it->y - it->x * h[i] + getG(i);
flag = 0;
tmp.x = getX(i);
tmp.y = getY(i);
tmp.k = 1e100;
it = H.insert(tmp).first;
set<node>::iterator x,y;
x=y=it;
++x;
if(it != H.begin() && x!=H.end())
{
y--;
if(det(y,it,x) < 0)
{
H.erase(it);
continue;
}
} //该点 偏离 凸包太远
x = it;
x++;
if(x != H.end())
{
set<node>::iterator xx = x;
xx++;
while(xx != H.end())
{
if(det(it,x,xx) > 0) //一旦满足 则后面也满足
break;
H.erase(x);
x = xx;
xx++;
}
}
y = it;
if(y != H.begin())
{
y--;
set<node>::iterator yy = y;
if(y != H.begin())
{
yy --;
while(1)
{
if(det(yy,y,it) > 0)
break;
H.erase(y);
if(yy == H.begin())
break;
y = yy;
yy--;
}
}
}
x = it;
x++; //对相邻的点 更新斜率
if(x==H.end())
const_cast<ld &>(it->k) = 1e100;
else
const_cast<ld &>(it->k) = ld(x->y - it->y)/ld(x->x - it->x);
y = it;
if(y != H.begin())
{
y--;
const_cast<ld &>(y->k) = ld(it->y - y->y)/ ld(it->x - y->x);
}
}
printf("%lld ",f[n]);
return 0;
}