线段树理解

闲话

当我觉得我学习算法刚刚从萌新到入门的时候，一类给定一个区间然后给定一系列操作的题彻底的打击了我，那时我才醒悟，编程路上，我一直是萌新。

前言

啥是线段树？

 线段树是一个具有树特性的数据结构，它是一颗二叉搜索树。如下图为区间[1,10]所建立的线段树

将每一个区间序列二分成小区间，线段树就存储小区间的信息，也就是每个小区间对应线段树中的一个结点。比如上图根节点对应[1,10]

• 对于每一个子节点而言，都表示整个序列中的一段子区间，如上图橙色节点；
• 对于每个叶子节点而言，都表示序列中的单个元素信息，如上图绿色节点；
• 子节点不断向自己的父亲节点传递信息，而父节点存储的信息则是它的每一个子节点信息的整合，也就是父亲是儿子们的并。

由于线段树的二分性质，对每一个子节点来说，左儿子的区间小于右儿子的区间，所以线段树也是平衡树。

有啥用？

将需要处理的信息看成一个个点，也就是叶子节点，然后通过父亲节点来将信息整合，做到通过树结构来进行操作对节点信息进行增删查改，大大降低复杂度。

最简单的应用就是记录区间是否被覆盖，随时查询当前被覆盖区间的总长度。

既然线段树利用区间二分建树，那么对子区间进行操作，只需要从根节点通过递归找到此区间即可，

一次操作时间肯定与树的高度有关，由于二叉树搜索树的关系，它的高度为log₂(n)，

所以完成一次操作的时间为O(log(n))。

那么回想前言中的题目：

　　给定区间n个数，n<=1000000，给定m个操作，m<=10000，对于每个操作，有两种情况

• 操作1：更新第k个数的值
• 操作2：查询区间[ l,r ]的和

　　用枚举法肯定超时，然而有了线段树，就可以用log₂(n)的时间完成每次操作，数据量很大时，不怕超时。

更多操作，接下来会更细致的讲解。

实现

建树

建一颗树，当然可以用递归和结构体数组。（还有非递归版本，暂时不给出）

int n;
struct node{
    int left,right,sum;
}node[4*n];//注意要开四倍空间

线段树是完全二叉树，一个序号为k的节点，它的左儿子序号为2*k，右儿子序号为2*k+1。、

即　　k   --->  k << 1 

　　　　 --->  k << 1 | 1

对于一个[ l,r ]区间，结构体中的left，表示此节点代表此区间的左端点l，right表示此区间的右端点r，sum表示此区间的总信息(这里是元素之和)

• 建树从node[1]开始，它是根节点，代表整个区间，所以left = l，right = r。
• 对于一个节点将它代表的区间分成两块，m=(l+r)/2，那么左儿子代表的区间为[l,m],右儿子代表的为[m+1,r]。

于是可以用递归来实现。

• 当一个节点的 left = right 时，表示它为一个叶子节点，没有儿子，不需要接着递归，而且它表示区间里的单个元素，所以此时要给sum赋值。
• 因为父亲节点的sum为儿子节点的并集，所以要通过回溯用已经赋过值的儿子节点来更新父亲节点的sum。
• 此外，追求方便以及对结构体的利用，可以在结构体里给出左端点left和右端点right，以至于在建树的时候保存每一个节点代表的区间。
• 用一个pushUp函数来表示将子节点信息整合到父节点

代码：

void pushUp(int n){
　　node[k].sum=node[2*k].sum+node[2*k+1].sum; //回溯过程，更新父亲节点
}

void build(int l,int r,int k){//[l,r]为初始区间，k为序号
　　 node[k].left=l;
　　 node[k].right=r;
    if(l==r){
        scanf("%d",node[k].sum);//给单个元素赋初值
        return ; // 遍历到子节点返回
    }
    int m=(l+r)/2;
    build(l,m,2*k);
    build(m+1,r,2*k+1);
    pushUp(k);　　//这里表示回溯函数
}

 具体实现看下图：

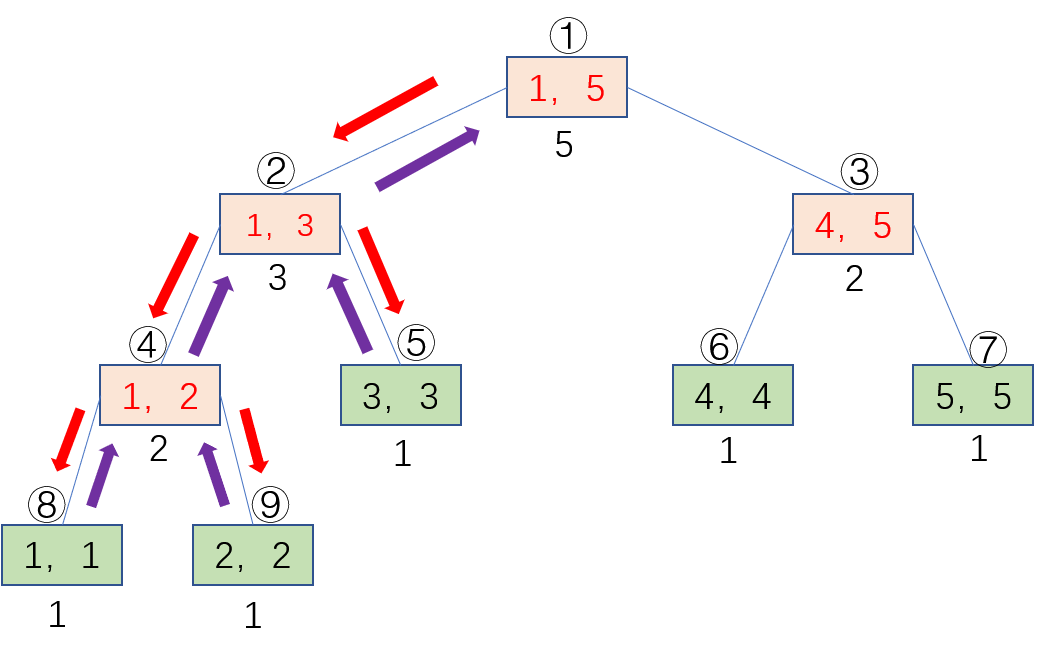
图中红色箭头表示build递归创造节点，紫色箭头表示pushUp回溯整合信息，

节点上面表示创造的序号，节点下面的数字表示节点代表的区间的总和。

为什么要开四倍空间？

这个问题很重要，不然随意开空间可能会导致溢出。

假设一颗线段树最下面一层最多有n个节点，是一个满二叉树，那么此线段树则有log₂(n)+1层。

但如果像[1,10]这样，不是满二叉树，那么(取整) log₂(n) < log₂(n)+1 ，所以这样的线段树最多有log₂(n)+2层。

而二叉树节点的个数为2^log₂(n)+2=4*n，所以要开4倍空间。

基本操作

单点查询与更新

根据上面所述：当某个节点的left==right时，它是一个叶子节点，也就是我们需要查询和修改的对象，于是可以通过递归线段树来找到需要的节点信息。