注:原创不易,转载请务必注明原作者和出处,感谢支持!
一 写在开头
本文内容为《组合数学》课程的最后一部分,容斥原理与鸽巢原理。这部分的内容分解图如下。
二 容斥原理
如下图所示。可以得到容斥原理的简单形式
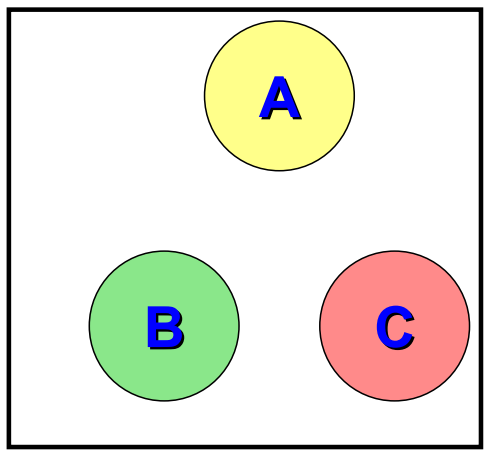
[�egin{equation}
�egin{split}
vert A cup B cup C vert &= vert A vert + vert B vert + vert C vert\
&- vert A cap B vert - vert A cap C vert - vert B cap C vert\
&- vert A cap B cap C vert
end{split}
end{equation}
]
全或形式的容斥原理如下
[�egin{equation}
�egin{split}
vert A_1 cup A_2 cup ... cup A_n vert &= sum_{i=1}^n vert A_i vert\
&-sum_{i=1}^n sum_{j > i} vert A_i cap A_j vert\
&+sum_{i=1}^n sum_{j > i} sum_{k > j} vert A_i cap A_j cap A_k vert\
&+...\
&+(-1)^{n-1} vert A_1 cap A_2 cap ... cap A_n vert
end{split}
end{equation}
]
全非形式的容斥原理(逐步淘汰原理)如下
假设在集合(S)上讨论(A_1, A_2, ..., A_n, vert S vert = N),则有
[�egin{equation}
�egin{split}
vert overline{A_1} cap overline{A_2} cap ... cap overline{A_n} vert = N - vert A_1 cup A_2 cup ... cup A_n vert
end{split}
end{equation}
]
(vert A_1 cup A_2 cup ... cup A_n vert)的计算公式上上面已给出。
容斥原理的第三种形式如下
[�egin{equation}
�egin{split}
vert overline{A_1} cap overline{A_2} cap ... cap overline{A_{n-1}} cap A_n vert &= vert A_n vert\
&-(vert A_1 cap A_n vert + vert A_2 cap A_n vert + ... + vert A_{n-1} cap A_n vert)\
&+(vert A_1 cap A_2 cap A_n vert + vert A_1 cap A_3 cap A_n vert + ... + vert A_1 cap A_{n-1} cap A_n vert + vert A_2 cap A_3 cap A_n vert + ... + vert A_{n-2} cap A_{n-1} cap A_n vert)\
&-(vert A_1 cap A_2 cap A_3 cap A_n vert + ... + vert A_{n-3} cap A_{n-2} cap A_{n-1} cap A_n vert)\
&+ ...\
&+(-1)^{n-1} vert A_1 cap A_2 cap ... cap A_n vert
end{split}
end{equation}
]
容斥原理求解方案数举例:求从([1, 500])的整数中,能够被3, 5, 7中的两个数整除的数的个数。
解:令
(A_1)表示([1, 500])中能被3整除的数的集合
(A_2)表示([1, 500])中能被5整除的数的集合
(A_3)表示([1, 500])中能被7整除的数的集合
则所求个数为$ vert A_1A_2 overline{A_3} vert + vert A_1A_3 overline{A_2} vert + vert A_2A_3 overline{A_1} vert$
三 鸽巢原理
鸽巢原理的简单形式:有(n+1)只鸽子飞进(n)个巢中,那么至少有一个鸽巢中有两只或两只以上的鸽子。
鸽巢原理的加强形式:设(m_1, m_2, ..., m_n)都是正整数,有(m_1 + m_2 + ... + m_n - n + 1)只鸽子飞进(n)个巢中,则下列(n)个命题中至少有一个成立。
或者第1个鸽巢,至少有(m_1)只鸽子
或者第2个鸽巢,至少有(m_2)只鸽子
...
或者第n个鸽巢,至少有(m_n)只鸽子
四 Ramsey定理
略
五 Burnside引理与波利亚定理
Burnside引理表述如下:
设(G)是(N={1, 2, ..., n})上的置换群,(G)在(N)上可引出不同的等价类,其不同等价类的个数为:
[l = frac{1}{vert G vert}[ c_1(a_1) + c_1(a_2) + c_1(a_i) + ... + c_1(a_g)]
]
其中(c_1(a_i))表示置换(a_i)作用后不变的方案个数。
波利亚定理表述如下:
设(N)是n个对象的集合,(overline{G} = {overline{P_1}, overline{P_2}, ... , overline{P_g}})是(N)上的置换群,用m种颜色(b_1, b_2, ..., b_m)对n个对象进行着色,设(C_k(overline{P}))为置换(overline{P})中(k-)循环的个数,令(S_k = b_1^k + b_2^k + ... + b_m^k~~ k=1,2,...,n)((S_k)为每种颜色允许出现k次),则具体着色方案数的多项式为:
[P = frac{1}{vert overline{G} vert} sum_{overline{p_i} in overline{G}} S_1^{C_1(overline{p_i})} cdot S_2^{C_2(overline{p_i})} cdot ... cdot S_n^{C_n(overline{p_i})}
]
展开合并同类项,则(b_1^{i_1}b_2^{i_2}...b_m^{i_m})前的系数即为具体着色方案数。

