今天讲了几个高级搜索算法:A* ,迭代加深,Alpha-Beta剪枝 以及线段树
A*算法
启发式搜索算法(A算法) :
在BFS算法中,若对每个状态n都设定估价函数 f(n)=g(n)+h(n),并且每次从Open表(队列)中选节点进行扩展时,都选取f值最小的节点,则该搜索算法为启发式搜索算法,又称A算法。
g(n) : 从起始状态到当前状态n的代价
h(n) : 从当前状态n到目标状态的估计代价
A算法中的估价函数若选取不当,则可能找不到解,或找到的解也不是最优解。因此,需要对估价函数做一些限制,使得算法确保找到最优解(步数,即状态转移次数最少的 解)。A*算法即为对估价函数做了特定限制, 且确保找到最优解的A算法。
A*算法:
f*(n) = g*(n) +h*(n)
f*(n) :从初始节点S0出发,经过节点n到达目标节点的最小步数 (真实值)。
g*(n): 从S0出发,到达n的最少步数(真实值)
h*(n): 从n出发,到达目标节点的最少步数(真实值)
估价函数f(n)则是f*(n)的估计值。
f (n)=g(n) +h(n) ,且满足以下限制:
A*算法 g(n)是从s0到n的真实步数(未必是最优的),因此: g(n)>0 且g(n)>=g*(n)
h(n)是从n到目标的估计步数。估计总是过于乐观的,即 h(n)<= h*(n) 且 h(n)相容,则A算法转变为A*算法。A*正确性证明略。
h(n)的相容:
如果h函数对任意状态s1和s2还满足: h(s1) <= h(s2) + c(s1,s2)
c(s1,s2)是s1转移到s2的步数,则称h是相容的。 h相容能确保随着一步步往前走,f递增,这样A*能更高效找 到最优解。
h相容 => g(s1) + h(s1) <= g(s1) + h(s2) +c(s1,s2) = g(s2)+h(S2) => f(s1) <= f(s2) 即f是递增的。
A*算法的搜索效率很大程度上取决于估价函数h(n)。一般说来,在 满足h(n)≤h*(n)的前提下,h(n)的值越大越好。

open=[Start] closed=[] while open不为空 { 从open中取出估价值f最小的结点n if n == Target then return 从Start到n的路径 // 找到了!!! else { for n的每个子结点x { if x in open { 计算新的f(x) 比较open表中的旧f(x)和新f(x) if 新f(x) < 旧f(x) { 删掉open表里的旧f(x),加入新f(x) } } else if x in closed { 计算新的f(x) 比较closed表中的旧f(x)和新f(x) if 新f(x) < 旧f(x) { remove x from closed add x to open } } // 比较新f(x)和旧f(x) 实际上比的就是新旧g(x),因h(x)相等 else { // x不在open,也不在close,是遇到的新结点 计算f(x) add x to open } } add n to closed } } //open表为空表示搜索结束了,那就意味着无解!
标准的启发式函数是曼哈顿距离(Manhattan distance)。考虑你的代价函数并找到从一个位置移动到邻近位置的最小代价D。
曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离,即D(I,J)=|XI-XJ|+|YI-YJ|。
对于一个具有正南正北、正东正西方向规则布局的城镇街道,从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离因此曼哈顿距离又称为出租车距离,曼哈顿距离不是距离不变量,当坐标轴变动时,点间的距离就会不同
推荐一个博客:https://blog.csdn.net/u013630349/article/details/53954164
例题:八数码问题
POJ上可用A*算法解决的题:1376 1324 1084 2449 1475
迭代加深搜索算法
算法思路 : 总体上按照深度优先算法方法进行
对搜索深度需要给出一个深度限制dm,当深度达到 了dm的时候,如果还没有找到解答,就停止对该分 支的搜索,换到另外一个分支继续进行搜索。 dm从1开始,从小到大依次增大(因此称为迭代加深 )(多次从起点出发)
迭代加深搜索是最优的,也是完备的,它能找到最优解又能节省空间(费时间)还可以不用判重。
例题:POJ 2286 The Rotation Game
Alpha-Beta剪枝 (极大极小搜索法)
假设:MAX和MIN对弈,轮到MAX走棋了,那么我们会遍历MAX的 每一个可能走棋方法,然后对于前面MAX的每一个走棋方法,遍历MIN的每一个走棋方法,然后接着遍历MAX的每一个走棋方法, …… 直到分出胜负或者达到了搜索深度的限制。若达到搜索深度限制时尚未分出胜负,则根据当前局面的形式,给出一个得分 ,计算得分的方法被称为估价函数,不同游戏的估价函数如何设 计和具体游戏相关。
在搜索树中,轮到MAX走棋的节点即为极大节点,轮到MIN走棋 的节点为极小节点。
方法:
1) 确定估价值函数,来计算每个棋局节点的估价值。对MAX方有利,估价值为正,对MAX方越有利,估价值越大。对MIN方有利,估价值为负, 对MIN方越有利,估价值越小。
2) 从当前棋局的节点要决定下一步如何走时,以当前棋局节点为根,生成一棵深度为n的搜索树。不妨总是假设当前棋局节点是MAX节点。
3) 用局面估价函数计算出每个叶子节点的估价值
4) 若某个非叶子节点是极大节点,则其估价值为其子节点中估价值最大的 那个节点的估价值
若某个非叶子节点是极小节点,则其估价值为其子节点中估价值最小 的那个节点的估价值
5) 选当前棋局节点的估价值最大的那个子节点,作为此步行棋的走法。
若结点x是Min节点,其兄弟节点(父节点相同的节点)中,已经求到的最大估价值是b(有些兄弟节点的估价值,可能还没有算出来),那么在对x的子节点进行考查的过程中,如果一旦发现某子节点的估价值 <=b,则不必再考查后面的x的子节点了。
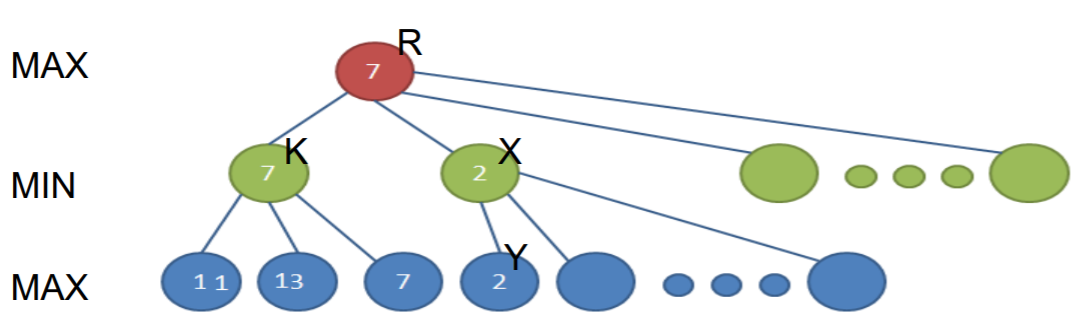
alpha剪枝
当搜索节点X时,若已求得某子节点Y的值为2,因为X是一个极小节点,那 么X节点得到的值肯定不大于2。因此X节点的子节点即使都搜索了,X节点 值也不会超过2。而节点K的值为7,由于R是一个Max节点,那么R的取值已 经可以肯定不会选X的取值了。因此X节点的Y后面子节点可以忽略,即图中 第三层没有数字的节点可被忽略。此即为alpha剪枝 ---- 因被剪掉的节点 是极大节点。相应的也有beta剪枝,即被剪掉的节点是极小节点。
beta剪枝
若结点x是Max节点,其兄弟节点(父节点相同的节点)中,已经求到的最小 估价值是a(有些兄弟节点的估价值,可能还没有算出来) 那么在对x的子节点进行考查的过程中,如果一旦发现某子节点的估价值 >= a,则不必再考查后面的x的子节点了。

function minimax(node, depth) // 指定当前节点和还要搜索的深度 // 如果胜负已分或者深度为零,使用评估函数返回局面得分 { if node is a terminal node or depth = 0 return the heuristic value of node // 如果轮到对手走棋,即node是极小节点,选择一个得分最小的走法 if the adversary is to play at node let α : = +∞ foreach child of node α : = min(α, minimax(child, depth-1)) // 如果轮到自己走棋,是极大节点,选择一个得分最大的走法 else{we are to play at node } let α : = -∞ foreach child of node α : = max(α, minimax(child, depth-1)) return α; } 具体的做法: int MinMax(int depth) //函数的评估都是以MAX方的角度来评估的 { if (SideToMove() == MAX_SIDE) return Max(depth); else return Min(depth); } int Max(int depth) { int best = -INFINITY; if (depth <= 0) return Evaluate(); GenerateLegalMoves(); while (MovesLeft()) //可以走 { MakeNextMove(); val = Min(depth - 1); UnmakeMove(); if (val > best) best = val; } return best; } int Min(int depth) { int best = INFINITY; // 注意这里不同于“最大”算法 if (depth <= 0) return Evaluate(); GenerateLegalMoves(); while (MovesLeft()) { MakeNextMove(); val = Max(depth - 1); UnmakeMove(); if (val < best) // 注意这里不同于“最大”算法 best = val; } return best; }
PS:红色字母处,随便写什么值都可以
在搜到底的情况下,infinity不一定是无穷大 infinity应该是主角赢的那 个状态(胜负已分的状态)的估价值,而-infinity应该是主角输的那个状态( 胜负已分的状态)的估价值。
必胜是指无论对方怎么走己方最后都能找到获胜方法,而不是不是自己怎么走都能获胜。
线段树
同一层的节点所代表的区间,相互不会重叠。同 一层节点所代表的区间,加起来是个连续的区间。
线段树是一棵二叉树,树中的每一个结 点表示了一个区间[a,b]。a,b通常是整数。
每一个叶子节点表示了一个单位区间(长度为1)。对于每一个非叶结点所表示的结点[a,b],其左儿子表示的区间为 [a,(a+b)/2],右儿子表示的区间为 [(a+b)/2+1,b](除法去尾取整)。
线段树的平分构造,实际上是用了二分的方法。若根节 点对应的区间是[a,b],那么它的深度为log2 (b-a+1) +1 (向上 取整)。
叶子节点的数目和根节点表示区间的长度相同.
线段树节点要么0度,要么2度, 因此若叶子节点数目为N, 则线段树总结点数目为2N-1
区间分解的时候,每层最多2个“终止节点”, 所以 终止节点总数也是log(n)量级的
线段树的深度不超过log2 (n)+1(向上取整,n是根节点 对应区间的长度)
线段树上,任意一个区间被分解后得到的“终止 节点”数目都是log(n)量级。线段树上更新叶子节点和进行区间分解时间 复杂度都是O(log(n))的
线段树的基本用途:线段树适用于和区间统计有关的问题。比如某些数据 可以按区间进行划分,按区间动态进行修改,而且还 需要按区间多次进行查询,那么使用线段树可以达到 较快查询速度。
用线段树解题,关键是要想清楚每个节点要存哪些信息 (当然区间起终点,以及左右子节点指针是必须的), 以及这些信息如何高效更新,维护,查询。不要一更新 就更新到叶子节点,那样更新效率最坏就可能变成O(n) 的了。
先建树,然后插入数据,然后更新,查询。
当数据太大时注意离散化:有时,区间的端点不是整数,或者区间太 大导致建树内存开销过大MLE ,那么就需要 进行“离散化”后再建树。
例题:1.POJ 3264 Balanced Lineup
2.POJ 3468 A Simple Problem with Integers
3.POJ 2528 Mayor's posters
