前言
学习完来自陈丹琦的《基于连通性状态压缩的动态规划问题》后来做个总结。
算法简介
插头 DP 就是一种基于连通性状态压缩的动态规划。
也就是说,在状态中需要记录若干个元素的联通情况。
插头 DP 有两个比较明显的特征:
-
以方格表为背景
-
状态总数为指数级,故数据范围在 (10) 左右。
详细的内容会结合着下面的例题来讲。
例题选讲
下面提供几道经典的题目:
例题1:BZOJ1814: Formula 1
(Large{ ext{Description:}})
给定一个 (m imes n) 的棋盘,有的格子中存在障碍,求经过所有非障碍格子的哈密顿回路个数。
数据范围:(2leq m,nleq 12)
(Large{ ext{Solution:}})
这题怎么做呢?
首先想到搜索,但是时间复杂度是 (O((mn)!)) 的,显然不太行……
于是考虑状态压缩!
下面先介绍两个基本概念:轮廓线、插头。
- 轮廓线:已决策格子与未决策格子的分界线;(下图中的红线)
- 插头:当前格子在插头方向与相邻格子相连。(下图中的箭头)
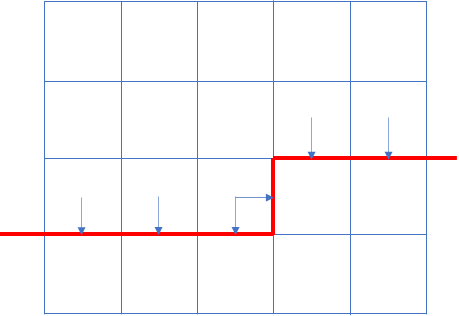
我们来从上到下,从左到右逐格转移。
考虑如下图所示的红色轮廓线向蓝色轮廓线转移时该怎么做。
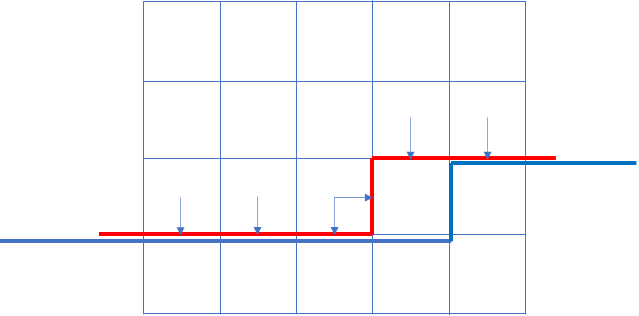
设 (f(i,j,S)) 表示刚刚转移完 ((i,j)),插头状态为 (S) 的方案总数。
那么想一下 (S) 应该如何表示?
最小表示法!
我们用一个 (n+1) 个数来表示 (S),具体如下:
- 轮廓线上的这一个格子如果无插头,该位为 (0);
- 轮廓线上的这一个格子如果有插头,该位与和这个格子联通的格子标记相同数字。
其中的非零数字从 (1) 开始取,每次取未取的最小数字。
但这么做在这题中依旧不够优秀,还有没有办法进行优化呢?
括号匹配序列!
为什么会这么想呢?
由于插头不会两两交叉且是两两匹配的,我们很自然地想到括号匹配问题。
接下来我们考虑用括号匹配序列来表示这个 (S),具体如下:
用一个三进制数来设置状态:
- (0):无插头状态
- (1):左括号插头
- (2):右括号插头
就下图而言,它表示出来的 (S) 是这样子的:((##)() o 100212)
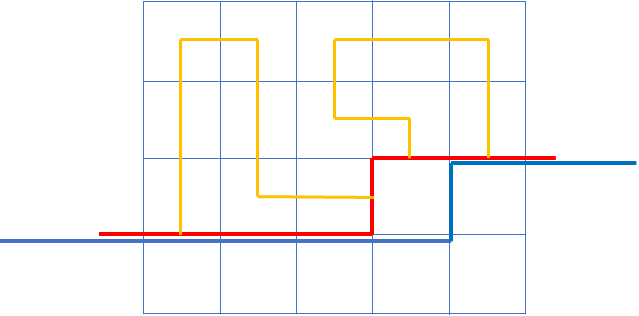
直到这里,我们把插头 DP 的基本概念学清楚了!
现在我们考虑怎么转移 (f(i,j,S))。
其实每次转移就是把当前决策格子的左插头改成下插头,上插头改成右插头。
于是我们把 ((i,j)) 的插头状态分类讨论一下。
1. 没有上插头和左插头,那么变成有下插头和右插头。
这种情况相当于构成一个新的连通块。
以下图为例,(S={1,0,0,0,0,2})。

由于有一条直线会穿过当前格,那么它是怎么被穿过的呢?
一定是这个格子多了下插头和右插头对吧。
此时的 (S'={1,0,0,1,2,2})。
2. 上插头和左插头中恰好只有 1 个。
此时相当于延续原来的连通分量。
什么意思呢?
我们同样举下图为例。

转移前,(S={1,0,0,0,2,0})。
那么当前格有两种决策:继续向下,向右拐。
而两种决策后得到的 (S') 分别为:
- 向下:(S'={1,0,0,2,0,0});
- 向右:(S'={1,0,0,0,2,0})。
我们发现其实这并不改变原来的括号匹配情况。
简单来讲,直接不改变 (S) 就行了。
3. 同时有上插头和左插头。
那么此时就相当于在这个格子结束,合并两个联通分量。
但实际上这个非常麻烦,我们再分成 4 类进行讨论。
3.1. 上插头和左插头均为 (
我们发现它影响的不只是这两个插头了,那怎么办呢?
考虑枚举这一位后的插头情况,直到遇见第一个不匹配成功的 ())
此时把它变成 (() 即可。
这么做为什么是对的呢?我们看一下下面的图。

原先,(S={0,1,1,2,0,2})。
当我们把当前格合并后,如果只是把 (1 o 0),那么 (S'={0,0,0,2,0,2})。
这样是不匹配的!
所以我们要找到右边第一个未匹配的 ()),并使 () o ()。
在这里,我们让 (S'={0,0,0,1,0,2}) 即可。
3.2. 上插头和左插头均为 )
同上,读者自行推导不难。
3.3. 上插头为 (,左插头为 )
我们考虑由于这两个必定会合起来,变成两个 (#)。
直接这么做有没有问题呢?
显然没有。
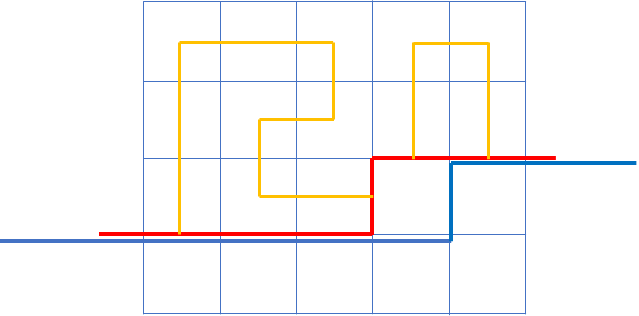
如上图所示,(S={1,0,0,2,1,2},S'={1,0,0,0,0,2})。
3.4. 上插头为 ),左插头为 (
这种情况只有在下面都是障碍方格时才可能会出现,特判一下即可。
对于刚刚提出来的例题,我们像上面这样转移即可。
时间复杂度:(O(3^{m+1}nm)),相比于搜索还是优化了非常多!
但其实它还有一点点的小常数可以优化。
在我们存 (S) 的时候其实是用 (3) 进制存的,这样没有用位运算,显然不够快。
于是我们干脆把它变成用 (4) 进制存。
这样虽然多了一个无用的数字,但可以用位运算实现,实测效率会高很多!
(Large{ ext{Code:}})
#include<bits/stdc++.h>
#define Re register
using namespace std;
typedef long long LL;
const int N=15;
const LL Hash=299987;
LL n,m,X,Y,inc[N],ans;
int mp[N][N];
LL now,lst;
LL hd[Hash+5],nxt[1<<25],que[2][1<<25],val[2][1<<25],cnt[2];
inline void insert(LL bit,LL num)
{
LL u=bit%Hash+1;
for(Re LL i=hd[u];i;i=nxt[i])
{
if(que[now][i]==bit)
{
val[now][i]+=num;
return;
}
}
cnt[now]++;
nxt[cnt[now]]=hd[u];
hd[u]=cnt[now];
que[now][cnt[now]]=bit;
val[now][cnt[now]]=num;
}
int main()
{
scanf("%d%d",&n,&m);
for(Re LL i=1;i<=n;i++)
{
char s[21];
scanf("%s",s+1);
for(Re LL j=1;j<=m;j++)
{
if(s[j]=='.')
{
mp[i][j]=1;
X=i,Y=j;
}
}
}
inc[0]=1;
for(Re LL i=1;i<=13;i++)
{
inc[i]=inc[i-1]<<2;
}
cnt[0]=1;
val[0][1]=1;
que[0][1]=0;
for(Re LL i=1;i<=n;i++)
{
for(Re LL j=1;j<=cnt[now];j++)
{
que[now][j]<<=2;
}
for(Re LL j=1;j<=m;j++)
{
memset(hd,0,sizeof hd);
lst=now;
now^=1;
cnt[now]=0;
for(Re LL k=1;k<=cnt[lst];k++)
{
LL bit,num,b1,b2;
bit=que[lst][k];
num=val[lst][k];
b1=(bit>>((j-1)<<1))%4;
b2=(bit>>(j<<1))%4;
if(!mp[i][j])
{
if(!b1&&!b2)
{
insert(bit,num);
}
}
else
{
if(!b1&&!b2)
{
if(mp[i+1][j]&&mp[i][j+1])
{
insert(bit+inc[j-1]+(inc[j]<<1),num);
}
}
if(!b1&&b2)
{
if(mp[i][j+1])
{
insert(bit,num);
}
if(mp[i+1][j])
{
insert(bit-inc[j]*b2+inc[j-1]*b2,num);
}
}
if(b1&&!b2)
{
if(mp[i+1][j])
{
insert(bit,num);
}
if(mp[i][j+1])
{
insert(bit-inc[j-1]*b1+inc[j]*b1,num);
}
}
if(b1==1&&b2==1)
{
LL K=1;
for(Re LL l=j+1;l<=m;l++)
{
if((bit>>(l<<1))%4==1)
{
K++;
}
if((bit>>(l<<1))%4==2)
{
K--;
}
if(!K)
{
insert(bit-inc[j]-inc[j-1]-inc[l],num);
break;
}
}
}
if(b1==2&&b2==2)
{
LL K=1;
for(Re LL l=j-2;l>=0;l--)
{
if((bit>>(l<<1))%4==1)
{
K--;
}
if((bit>>(l<<1))%4==2)
{
K++;
}
if(!K)
{
insert(bit-(inc[j]<<1)-(inc[j-1]<<1)+inc[l],num);
break;
}
}
}
if(b1==2&&b2==1)
{
insert(bit-(inc[j-1]<<1)-inc[j],num);
}
if(i==X&&j==Y)
{
ans+=num;
}
}
}
}
}
printf("%lld",ans);
return 0;
}
例题2:Eat the Trees
(Large{ ext{Description:}})
给出 (n imes m) 的方格表,有些格子不能铺线,其它格子必须铺,可以形成多个闭合回路。问有多少种铺法?
数据范围:(2leq nleq 12)。
(Large{ ext{Solution:}})
这题与之前的例题类似,只是在这题中,它可以形成多条回路。
正因为如此,所以我们没必要用括号序列。
为什么呢?
因为括号序列是为了防止回路提前闭合才使用的,而这题不需要。
那就直接存轮廓线上有的插头即可。
现在我们来考虑如何转移状态。
-
左 0 上 0 ( o) 右 1 下 1,即加了个转角。
-
左 1 上 1 ( o) 右 0 下 0,即闭合了一段回路。
-
左 0 上 1 ( o) 右 1 下 0 或 右 0 下 1,即向右转弯或继续向下。
-
左 1 上 0 ( o) 右 1 下 0 或 右 0 下 1,即继续向下或向右转弯。
上述的情况 (3,4) 本质相同,可以归为一类。
这样就完成了本题。
#include<bits/stdc++.h>
#define Re register
using namespace std;
typedef long long LL;
const int N=15;
int T,n,m,mp[N][N];
LL dp[2][1<<20];
inline int rd()
{
char ch=getchar();
int x=0,f=1;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline void change(int& cur,int pos,int val)
{
if(val==1) cur=cur|(1<<(pos-1));
else cur=cur&(~(1<<(pos-1)));
}
int main()
{
scanf("%d",&T);
while(T--)
{
memset(dp,0,sizeof dp);
n=rd();
m=rd();
for(Re int i=1;i<=n;i++)
{
for(Re int j=1;j<=m;j++)
{
mp[i][j]=rd();
}
}
int lst=0,now=1;
dp[0][0]=1;
for(Re int i=1;i<=n;i++)
{
for(Re int j=1;j<=m;j++)
{
for(Re int k=0;k<(1<<(m+1));k++)
{
int cur=k;
int L=k&(1<<(j-1));
int U=k&(1<<j);
if(!mp[i][j])
{
if(!L&&!U)
{
dp[now][k]+=dp[lst][k];
}
}
else
{
if(!L&&!U)
{
change(cur,j,1);
change(cur,j+1,1);
dp[now][cur]+=dp[lst][k];
}
if(L&&U)
{
change(cur,j,0);
change(cur,j+1,0);
dp[now][cur]+=dp[lst][k];
}
if((L&&!U)||(!L&&U))
{
change(cur,j,1);
change(cur,j+1,0);
dp[now][cur]+=dp[lst][k];
change(cur,j,0);
change(cur,j+1,1);
dp[now][cur]+=dp[lst][k];
}
}
}
memset(dp[lst],0,sizeof dp[lst]);
lst^=1,now^=1;
}
for(Re int j=0;j<(1<<m);j++)
{
dp[now][j<<1]=dp[lst][j];
}
memset(dp[lst],0,sizeof dp[lst]);
lst^=1,now^=1;
}
printf("%lld
",dp[lst][0]);
}
return 0;
}