1.用Newton迭代法求方程  的第一个正根.
的第一个正根.
作者:凯鲁嘎吉 - 博客园http://www.cnblogs.com/kailugaji/
newton.m:
function x1=newton(x0,eps)
format long
format compact
x1=x0-dao(x0);
while abs(x1-x0)>eps
x0=x1;
x1=x0-dao(x0);
end
dao.m:
function y=dao(x)
y=tan(x)-exp(x);
y1=tan(x)^2 - exp(x) + 1;
y=y/y1;
结果:
>> x1=newton(1,1e-6)
x1 =
1.306326940423080
2.作矩阵  的LU分解.
的LU分解.
lu12.m:
function [l,u]=lu12(a,n)
for k=1:n-1
for i=k+1:n
a(i,k)=a(i,k)/a(k,k);
for j=k+1:n
a(i,j)=a(i,j)-a(i,k)*a(k,j);
end
end
end
l=eye(n);
u=zeros(n,n);
for k=1:n
for i=k:n
u(k,i)=a(k,i);
end
end
for k=1:n
for j=1:k-1
l(k,j)=a(k,j);
end
end
结果:
>> a=[4 1 1 1;8 5 1 3;12 -3 7 2;4 10 2 7];
>> [l,u]=lu12(a,4)
l =
1 0 0 0
2 1 0 0
3 -2 1 0
1 3 2 1
u =
4 1 1 1
0 3 -1 1
0 0 2 1
0 0 0 1
3.用Jacobi迭代法求解方程组 , 其中
, 其中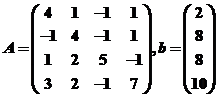 .
.
jacobi.m:
function x=jacobi(a,b,x0,n,tol,m)
x=zeros(n,1);
for k=0:m
for i=1:n
s=0;
for j=1:n
if j~=i
s=s+a(i,j)*x0(j,1);
end
end
x(i,1)=(b(i,1)-s)/a(i,i);
if norm(x-x0,inf)<tol
break;
end
x0(i,1)=x(i,1);
end
end
结果:
>> a=[4 1 -1 1;-1 4 -1 1;1 2 5 -1;3 2 -1 7];
>> b=[2 8 8 10]';
>> x0=[0 0 0 0]';
>> x=jacobi(a,b,x0,4,1e-6,50)
x =
-0.000000983453000
2.000001278748222
0.999997309599650
0.999999964663427
4.用复化的辛甫生方法计算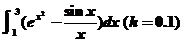 .
.
simpson.m:
function [SI,Y,esp]=simpson(a,b,m)
%a,b为区间左右端点,xps(x)为求积公式,m*2等分区间长度
h=(b-a)/(2*m);
SI0=xps(a)+xps(b);
SI1=0;
SI2=0;
for i=1:((2*m)-1)
x=a+i*h;
if mod(i,2)==0
SI2=SI2+xps(x);
else
SI1=SI1+xps(x);
end
end
SI=vpa(h*(SI0+4*SI1+2*SI2)/3,10);
syms x
Y=vpa(int(xps(x),x,a,b),10);
esp=abs(Y-SI);
xps.m:
function y=xps(x)
y=exp(x^2)-sin(x)/x;
结果:
>> [SI,Y,esp]=simpson(1,3,10)
SI =
1443.251264
Y =
1442.179902
esp =
1.0713621257845176160117262043059
5.用改进的尤拉法解方程 
euler22.m:
function [B1,B2]=euler22(a,b,n,y0)
%欧拉法解一阶常微分方程
%初始条件y0
h = (b-a)/n; %步长h
%区域的左边界a
%区域的右边界b
x = a:h:b;
m=length(x);
%改进欧拉法
y = y0;
for i=2:m
y(i)=y(i-1)+h/2*( oula2(x(i-1),y(i-1))+oula2(x(i),y(i-1))+h*(oula2(x(i-1),x(i-1))));
B1(i)=x(i);
B2(i)=y(i);
end
plot(x,y,'m-');
hold on;
%精确解用作图
xx = x;
f = dsolve('Dy=exp(x-y)+(x^2)*exp(-y)','y(0)=0','x');%求出解析解
y = subs(f,xx); %将xx代入解析解,得到解析解对应的数值
plot(xx,y,'k--');
legend('改进欧拉法','解析解');
oula2.m:
function f=oula2(x,y)
f=exp(x-y)+(x^2)*exp(-y);
结果:
>> [B1,B2]=euler22(0,1,10,0)
B1 =
Columns 1 through 7
0 0.100000000000000 0.200000000000000 0.300000000000000 0.400000000000000 0.500000000000000 0.600000000000000
Columns 8 through 11
0.700000000000000 0.800000000000000 0.900000000000000 1.000000000000000
B2 =
Columns 1 through 7
0 0.110758545903782 0.222173861791736 0.335492896789537 0.451351722029268 0.569931474513367 0.691088488902808
Columns 8 through 11
0.814464555075657 0.939577860819895 1.065894210026593 1.192879090561291

6.(1) 用 拟合下列数据:
拟合下列数据:
| x |
2.36 |
3.73 |
5.951 |
8.283 |
| f(x) |
14.1 |
16.2 |
18.3 |
21.4 |
LSM1.m:
function [a,b,c]=LSM1(x,y,m) %x,y为序列长度相等的数据向量,m为拟合多项式次数
format short;
A=zeros(m+1,m+1);
for i=0:m
for j=0:m
A(i+1,j+1)=sum(x.^(i+j));
end
b(i+1)=sum(x.^i.*y);
end
a=A';
p=fliplr(a');
%y=p[0]*x^m+p[1]*x^(m-1)+...+p[m-1]*x+p[m];
a=p(3);
b=p(2);
c=p(1);
结果:
>> x=[2.36 3.73 5.951 8.283];
>> y=[14.1 16.2 18.3 21.4];
>> [a,b,c]=LSM1(x,y,2)
a =
11.4457
b =
1.1866
c =
8.1204e-04
(2) 按如下插值原则,求Newton插值多项式:
| x |
2.36 |
3.73 |
5.951 |
8.283 |
| f(x) |
14.1 |
16.2 |
18.3 |
21.4 |
说明:最后,一定给清楚各多项式的系数!
newploy.m:
function [A,C,L,wcgs,Cw]= newploy(X,Y)
n=length(X); A=zeros(n,n); A(:,1)=Y';
q=1.0; c1=1.0;
for j=2:n
for i=j:n
A(i,j)=(A(i,j-1)- A(i-1,j-1))/(X(i)-X(i-j+1));
end
b=poly(X(j-1));q1=conv(q,b); c1=c1*j; q=q1;
end
C=A(n,n); b=poly(X(n)); q1=conv(q1,b);
for k=(n-1):-1:1
C=conv(C,poly(X(k))); d=length(C); C(d)=C(d)+A(k,k);
end
L(k,:)=poly2sym(C); Q=poly2sym(q1);
syms M
wcgs=M*Q/c1; Cw=q1/c1;
结果:
>> x=[2.36 3.73 5.951 8.283];
>> y=[14.1 16.2 18.3 21.4];
>> [A,C,L,wcgs,Cw]= newploy(x,y)
A =
14.1000 0 0 0
16.2000 1.5328 0 0
18.3000 0.9455 -0.1636 0
21.4000 1.3293 0.0843 0.0418
C =
0.0418 -0.6674 4.4138 6.8506
L =
(3015319848353441*x^3)/72057594037927936 - (3005803726105311*x^2)/4503599627370496 + (4969523982821561*x)/1125899906842624 + 7713109820116169/1125899906842624
wcgs =
(M*(x^4 - (5081*x^3)/250 + (1273498286182623*x^2)/8796093022208 - (7485266609524121*x)/17592186044416 + 7633404131354389/17592186044416))/24
Cw =
0.0417 -0.8468 6.0325 -17.7287 18.0795
newpoly2.m:
function y= newpoly2(X,Y,x)
n=length(X); m=length(x);
for t=1:m
z=x(t); A=zeros(n,n);A(:,1)=Y';
q1=1.0; c1=1.0;
for j=2:n
for i=j:n
A(i,j)=(A(i,j-1)- A(i-1,j-1))/(X(i)-X(i-j+1));
end
q1=abs(q1*(z-X(j-1)));c1=c1*j;
end
C=A(n,n);q1=abs(q1*(z-X(n)));
for k=(n-1):-1:1
C=conv(C,poly(X(k)));d=length(C); C(d)=C(d)+A(k,k);
end
y(k)= polyval(C, z);
end
结果:
>> y= newpoly2(x,y,15)
y =
64.1181