可持久化线段树
可持久化概念
一个数据结构被认为是可持久化的,当且仅当它满足下面的性质:
- 可以回溯到某个历史版本(包括分支)。
- 可以修改某个历史版本(包括分支)并产生新的分支。
不太懂的 \(\rm{dalao}\) 们可以联想 \(\rm{git}\) 的版本控制。(如果没有用过 \(\rm{git}\) 的话...当我没说)
可持久化数组
这个是一切可持久化数据结构的基础。
现在有一个长度为 \(n\) 的序列,依次执行 \(m\) 个操作,第 \(i\) 个操作为下列两种操作之一:
- 输入 \(v_i,1,p_i,w_i\),将第 \(v_i\) 次操作完成后的序列复制,然后将 \(p_i\) 处修改为 \(w_i\),作为第 \(i\) 次操作后的序列。
- 输入 \(v_i,2,p_i\),将第 \(v_i\) 次操作完成后的序列复制为第 \(i\) 次操作后的序列,然后输出 \(p_i\) 处的值。
\(1 \leq n, m \leq 10^6\)
这个题目描述已经把 \(O(n^2)\) 的暴力描述出来了,就不说了。此时,我们需要减少复制的次数。
首先对初始状态的序列建一个线段树的结构,代表区间 \([p,p]\) 的叶子节点表示原序列中的 \(p\) 处,根节点保存版本编号,其他节点不记录除了代表区间以外的其他信息。比如对于序列 \([1,4,2,3,5,2]\) ,建立下面的线段树:
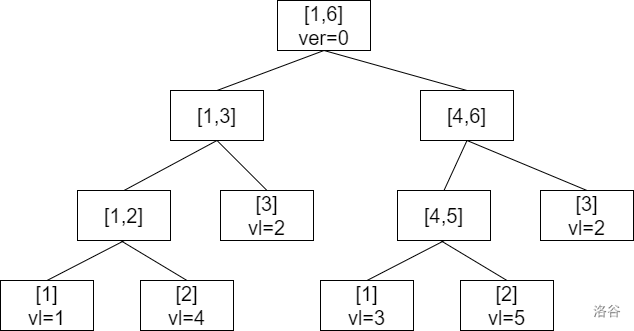
接下来考虑在 \(0\) 版本的基础上,将 \(3\) 号位置修改为 \(5\) ,这时候,我们要尽可能减少复制的节点数量,那么我们可以只复制版本 \(0\) 中 \(3\) 号叶子节点到根的路径上的所有节点,就像下面这个样子:

这时候,想要找到版本 \(1\) 中某个位置的值,只需要从版本 \(1\) 的根节点往下递归找就行了。
同理,在版本 \(1\) 的基础上将 \(2\) 号位置修改为 \(2\) ,那么只需要将版本 \(1\) 中二号叶子节点到根节点的路径上的点复制一遍,然后加边就可以了,像下面这个样子:
 ]
]
每次复制节点的个数为 \(O(\log_2n)\),因此总的时间复杂度为 \(O(n\log_2 n)\) 。
这里放出本人丑陋的代码:
const int maxn = 1e6 + 5, maxm = maxn * 20;
struct ST {
struct STNode { int ls, rs, vl; } nd[maxm];
int nd_cnt;
//创建初始版本
void init(int& p, int l, int r, int* ls) {
p = ++nd_cnt;
if (l == r) { nd[p].vl = ls[l]; return ; }
int mid = (l + r) >> 1;
init(nd[p].ls, l, mid, ls), init(nd[p].rs, mid + 1, r, ls);
}
//直接复制版本
void cpy(int& p, int q) { p = ++nd_cnt, nd[p].ls = nd[q].ls, nd[p].rs = nd[q].rs; }
//新增一个版本,并将 pos 的值修改为 val
void chg(int& p, int q, int l, int r, int pos, int val) {
cpy(p, q);
if (l == r) { nd[p].vl = val; return ; }
int mid = (l + r) >> 1;
if (pos <= mid) chg(nd[p].ls, nd[q].ls, l, mid, pos, val);
else chg(nd[p].rs, nd[q].rs, mid + 1, r, pos, val);
}
//询问
int ask(int p, int l, int r, int pos) {
if (l == r) return nd[p].vl;
int mid = (l + r) >> 1;
if (pos <= mid) return ask(nd[p].ls, l, mid, pos);
else return ask(nd[p].rs, mid + 1, r, pos);
}
int rt[maxn];
} st;
int n, m, a[maxn];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
st.init(st.rt[0], 1, n, a);
for (int i = 1; i <= m; i++) {
int v, t, loc, val; scanf("%d%d%d", &v, &t, &loc);
if (t == 1) scanf("%d", &val), st.chg(st.rt[i], st.rt[v], 1, n, loc, val);
else st.cpy(st.rt[i], st.rt[v]), printf("%d\n", st.ask(st.rt[i], 1, n, loc));
}
return 0;
}
简单的可持久化线段树
现在考虑增加两个操作,询问某个版本的区间和以及基于某个版本的区间加。
对于询问,可以直接在先前的代码中非叶子节点记录一下区间和。
对于区间加,显然不能像普通的线段树那样传标记,因此要引入标记永久化。
标记永久化
\(\rm{PS}\):这部分代码可能有错
这个东西听起来十分牛逼,但实际上打标记但是不下传标记,而是在询问的时候使用函数传参的方式临时计算标记对儿子节点的影响。
接下来首先写出结构体的定义和询问的代码(因为比较容易写):
struct ST {
struct STNode { int ls, rs, vl, tag; } nd[maxm];
...//这里是之前写的代码
void cpy(int& p, int q) { //重写一下复制
p = ++nd_cnt;
nd[p].ls = nd[q].ls, nd[p].rs = nd[q].rs, nd[p].vl = nd[q].vl, nd[p].tag = nd[q].tag;
}
int ask(int p, int l, int r, int ql, int qr, int tag) {
if (ql > r || qr < l) return 0;
//在计算子区间的贡献时手动计算一路下来的所有标记对这个子区间的影响
if (ql <= l && r <= qr) return nd[p].vl + tag * (r - l + 1);
//这里没有像普通线段树那样下传标记
int mid = (l + r) >> 1;
//模拟下传标记
tag += nd[o].tag;
return ask(nd[o].ls, l, mid, ql, qr, tag) + ask(nd[o].rs, mid + 1, r, ql, qr, tag);
}
...
};
接下来要写修改部分的代码,这里因为不能使用子节点的信息(修改之前的标记没有下传,因此子节点此时的 \(\rm{vl}\) 并不是真正的 \(\rm{vl}\) ),这时候更新节点的 \(\rm{vl}\) 时要靠整个修改区间的信息和自己的信息。下面依然给出代码:
struct ST {
...
void chg_segadd(int& p, int q, int l, int r, int ql, int qr, int val) {
cpy(p, q);
//使用自己的信息更新 vl
nd[p].vl += val * (min(qr, r) - max(ql, l) + 1);
if (ql <= l && r <= qr) {
nd[p].tag += val; //打标记
return ;
}
int mid = (l + r) >> 1;
//在这里控制越界,防止复制过多的节点
if (ql <= mid) chg_segadd(nd[p].ls, nd[q].ls, l, mid, ql, qr, val);
if (qr > mid) chg_segadd(nd[p].rs, nd[q].rs, mid + 1, r, ql, qr, val);
}
};
主席树
主席树本质上是一种利用可持久化线段树求出静态(没有修改)的区间第 \(k\) 小值的方法。
对于一个序列 \(A_{1...n}\) ,建立一颗可持久化的权值线段树,然后从 \(A_1\) 到 \(A_n\) 逐个加入到权值线段树,每插入一个序列中的值,就作为一个版本,那么很显然,现在我们有了对于任意一个 \(A\) 的前缀,值在某个区间的元素的个数,那么对于任何一个 \(A\) 的连续子段 \(A_{l...r}\) 中值在某个区间的元素的个数,就可以使用 \(A_r\) 的个数减去 \(A_{l-1}\) 的个数。因此可以写出下面的代码:
struct ST {
...
//这里的 n 是指 A 中不同的值的个数
//若想求出 [l,r] 中第 k 大的元素,应调用 find_kth(rt[r], rt[l - 1], 1, n, k)
int find_kth(int p, int q, int l, int r, int k) {
if (l == r) return l;
int mid = (l + r) >> 1;
if (nd[nd[p].ls].vl - nd[nd[q].ls].vl >= k)
return find_kth(nd[p].ls, nd[q].ls, l, mid, k);
else return find_kth(nd[p].rs, nd[q].rs, mid + 1, r, k - (nd[nd[p].ls].vl - nd[nd[q].ls].vl));
}
}
可持久化并查集
所谓可持久化并查集,就是用可持久化数组维护按秩合并的并查集的 \(\rm{fa}\) 数组和 \(\rm{dep}\) 数组。(简单粗暴)
直接给出源代码吧:
const int maxn = 1e5 + 5, maxm = 2e5 + 5;
namespace UFS {
struct Node { int ls, rs, fa, dep; } nd[(maxm + maxn) * 20];
int sz, nd_cnt, rt[maxm];
inline void cpy(int& gl, int src) { gl = ++nd_cnt, nd[gl] = nd[src]; }
void chg_fa(int& p, int q, int l, int r, int pos, int vl) {
cpy(p, q);
if (l == r) { nd[p].fa = vl; return ; }
int mid = (l + r) >> 1;
if (pos <= mid) chg_fa(nd[p].ls, nd[q].ls, l, mid, pos, vl);
else chg_fa(nd[p].rs, nd[q].rs, mid + 1, r, pos, vl);
}
void inc_dep(int p, int l, int r, int pos) {
if (l == r) { nd[p].dep++; return ; }
int mid = (l + r) >> 1;
if (pos <= mid) inc_dep(nd[p].ls, l, mid, pos);
else inc_dep(nd[p].rs, mid + 1, r, pos);
}
//这里返回的是 pos 处对应的叶子节点
int get_nd(int p, int l, int r, int pos) {
if (l == r) return p;
int mid = (l + r) >> 1;
if (pos <= mid) return get_nd(nd[p].ls, l, mid, pos);
else return get_nd(nd[p].rs, mid + 1, r, pos);
}
void init(int& o, int l, int r) {
o = ++nd_cnt;
if (l == r) { nd[o].fa = l, nd[o].dep = 1; return ; }
int mid = (l + r) >> 1;
init(nd[o].ls, l, mid), init(nd[o].rs, mid + 1, r);
}
int get_fand(int ver, int v) {
int fand = get_nd(rt[ver], 1, sz, v);
if (nd[fand].fa == v) return fand;
return get_fand(ver, nd[fand].fa);
}
int check(int n_ver, int o_ver, int u, int v) {
int fand1 = get_fand(o_ver, u), fand2 = get_fand(o_ver, v);
cpy(rt[n_ver], rt[o_ver]);
return fand1 == fand2;
}
void merge(int n_ver, int o_ver, int u, int v) {
int fand1 = get_fand(o_ver, u), fand2 = get_fand(o_ver, v);
if (fand1 == fand2) {
cpy(rt[n_ver], rt[o_ver]);
return ;
}
if (nd[fand1].dep > nd[fand2].dep) swap(fand1, fand2);
chg_fa(rt[n_ver], rt[o_ver], 1, sz, nd[fand1].fa, nd[fand2].fa);
if (nd[fand1].dep == nd[fand2].dep) inc_dep(rt[n_ver], 1, sz, nd[fand2].fa);
}
}
int main() {
int n, m; scanf("%d%d", &n, &m);
UFS::sz = n, UFS::init(UFS::rt[0], 1, n);
for (int i = 1; i <= m; i++) {
int opt, a, b; scanf("%d", &opt);
if (opt == 1) scanf("%d%d", &a, &b), UFS::merge(i, i - 1, a, b);
else if (opt == 2) scanf("%d", &a), UFS::cpy(UFS::rt[i], UFS::rt[a]);
else scanf("%d%d", &a, &b), printf("%d\n", UFS::check(i, i - 1, a, b));
}
return 0;
}