转载请注明出处,部分内容引自banananana大神的博客
~~别说你不知道什么是树~~╮(─▽─)╭(帮你百度一下)
先来回顾两个问题:
1,将树从x到y结点最短路径上所有节点的值都加上z
这也是个模板题了吧
我们很容易想到,树上差分可以以O(n+m)的优秀复杂度解决这个问题
2,求树从x到y结点最短路径上所有节点的值之和
lca大水题,我们又很容易地想到,dfs O(n)预处理每个节点的dis(即到根节点的最短路径长度)
然后对于每个询问,求出x,y两点的lca,利用lca的性质distance ( x , y ) = dis ( x ) + dis ( y ) - 2 * dis ( lca )求出结果
时间复杂度O(mlogn+n)
现在来思考一个bug:
如果刚才的两个问题结合起来,成为一道题的两种操作呢?
刚才的方法显然就不够优秀了(每次询问之前要跑dfs更新dis)
树链剖分华丽登场
树剖是通过轻重边剖分将树分割成多条链,然后利用数据结构来维护这些链(本质上是一种优化暴力)
首先明确概念:
重儿子:父亲节点的所有儿子中子树结点数目最多(size最大)的结点;
轻儿子:父亲节点中除了重儿子以外的儿子;
重边:父亲结点和重儿子连成的边;
轻边:父亲节点和轻儿子连成的边;
重链:由多条重边连接而成的路径;
轻链:由多条轻边连接而成的路径;
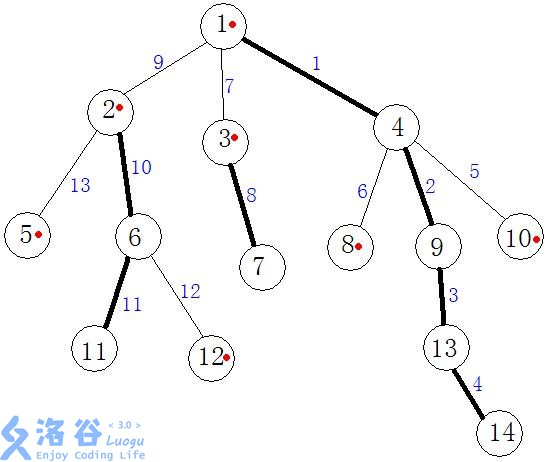
比如上面这幅图中,用黑线连接的结点都是重结点,其余均是轻结点,
2-11就是重链,2-5就是轻链,用红点标记的就是该结点所在重链的起点,也就是下文提到的top结点,
还有每条边的值其实是进行dfs时的执行序号。
变量声明:
const int maxn=1e5+10;
struct edge{
int next,to;
}e[2*maxn];
struct Node{
int sum,lazy,l,r,ls,rs;
}node[2*maxn];
int rt,n,m,r,a[maxn],cnt,head[maxn],f[maxn],d[maxn],size[maxn],son[maxn],rk[maxn],top[maxn],id[maxn];
| 名称 | 解释 |
| f[u] | 保存结点u的父亲节点 |
| d[u] | 保存结点u的深度值 |
| size[u] | 保存以u为根的子树节点个数 |
| son[u] | 保存重儿子 |
| rk[u] | 保存当前dfs标号在树中所对应的节点 |
| top[u] | 保存当前节点所在链的顶端节点 |
| id[u] | 保存树中每个节点剖分以后的新编号(DFS的执行顺序) |
我们要做的就是(树链剖分的实现):
1,对于一个点我们首先求出它所在的子树大小,找到它的重儿子(即处理出size,son数组),
解释:比如说点1,它有三个儿子2,3,4
2所在子树的大小是5
3所在子树的大小是2
4所在子树的大小是6
那么1的重儿子是4
ps:如果一个点的多个儿子所在子树大小相等且最大
那随便找一个当做它的重儿子就好了
叶节点没有重儿子,非叶节点有且只有一个重儿子
2,在dfs过程中顺便记录其父亲以及深度(即处理出f,d数组),操作1,2可以通过一遍dfs完成
void dfs1(int u,int fa,int depth) //当前节点、父节点、层次深度
{
f[u]=fa;
d[u]=depth;
size[u]=1; //这个点本身size=1
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v==fa)
continue;
dfs1(v,u,depth+1); //层次深度+1
size[u]+=size[v]; //子节点的size已被处理,用它来更新父节点的size
if(size[v]>size[son[u]])
son[u]=v; //选取size最大的作为重儿子
}
}
//进入
dfs1(root,0,1);

dfs跑完大概是这样的,大家可以手动模拟一下
3,第二遍dfs,然后连接重链,同时标记每一个节点的dfs序,并且为了用数据结构来维护重链,我们在dfs时保证一条重链上各个节点dfs序连续(即处理出数组top,id,rk)
void dfs2(int u,int t) //当前节点、重链顶端
{
top[u]=t;
id[u]=++cnt; //标记dfs序
rk[cnt]=u; //序号cnt对应节点u
if(!son[u])
return;
dfs2(son[u],t);
/*我们选择优先进入重儿子来保证一条重链上各个节点dfs序连续,
一个点和它的重儿子处于同一条重链,所以重儿子所在重链的顶端还是t*/
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v!=son[u]&&v!=f[u])
dfs2(v,v); //一个点位于轻链底端,那么它的top必然是它本身
}
}
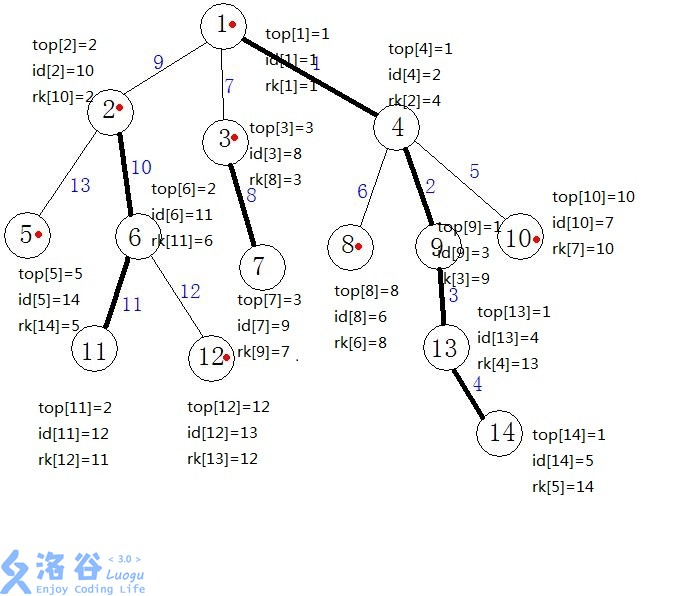
dfs跑完大概是这样的,大家可以手动模拟一下
4,两遍dfs就是树链剖分的主要处理,通过dfs我们已经保证一条重链上各个节点dfs序连续,那么可以想到,我们可以通过数据结构(以线段树为例)来维护一条重链的信息
回顾上文的那个题目,修改和查询操作原理是类似的,以查询操作为例,其实就是个LCA,不过这里使用了top来进行加速,因为top可以直接跳转到该重链的起始结点,轻链没有起始结点之说,他们的top就是自己。需要注意的是,每次循环只能跳一次,并且让结点深的那个来跳到top的位置,避免两个一起跳从而擦肩而过。
int sum(int x,int y)
{
int ans=0,fx=top[x],fy=top[y];
while(fx!=fy) //两点不在同一条重链
{
if(d[fx]>=d[fy])
{
ans+=query(id[fx],id[x],rt); //线段树区间求和,处理这条重链的贡献
x=f[fx],fx=top[x]; //将x设置成原链头的父亲结点,走轻边,继续循环
}
else
{
ans+=query(id[fy],id[y],rt);
y=f[fy],fy=top[y];
}
}
//循环结束,两点位于同一重链上,但两点不一定为同一点,所以我们还要统计这两点之间的贡献
if(id[x]<=id[y])
ans+=query(id[x],id[y],rt);
else
ans+=query(id[y],id[x],rt);
return ans;
}
大家如果明白了树链剖分,也应该有举一反三的能力(反正我没有),修改和LCA就留给大家自己完成了
5,树链剖分的时间复杂度
树链剖分的两个性质:
1,如果(u, v)是一条轻边,那么size(v) < size(u)/2;
2,从根结点到任意结点的路所经过的轻重链的个数必定都小于logn;
可以证明,树链剖分的时间复杂度为O(nlogn)
例题:
树链剖分模板
就是刚才讲的
上代码:
 View Code
View Code