1.三角形数： n(n+1)/2
性质： (1)所有大于3的三角形数都不是质数
(2)所有偶完全数都是三角形数
2.四边形数（平方数）n*n
(1)拉格朗日四平方和定理
1）每个自然数均可表示成4个平方数之和。
2）3个平方数之和不能表示形式如4k(8n+ 7)的数。
3）如果在一个正整数的因数分解式中，没有一个数有形式如4k+3的质数次方，该正整数可以表示成两个平方数之和。
(2)
在十进制中，平方数只能以 00，1，4，6，9 或 25 结尾：
若一个数以 0 结尾，它的平方数以 00 结尾，且其他数字也构成一个平方数
若一个数以 1 或 9 结尾，它的平方数以 1 结尾，且其他数字构成的数能被 4 整除
若一个数以 2 或 8 结尾，它的平方数以 4 结尾，且其他数字构成一个偶数
若一个数以 3 或 7 结尾，它的平方数以 9 结尾，且其他数字构成的数能被 4 整除
若一个数以 4 或 6 结尾，它的平方数以 6 结尾，且其他数字构成一个奇数
若一个数以 5 结尾，它的平方数以 25 结尾，且前面的一位或两位数字数字必定为 0，2，06，56 之一
(3)每4个连续的自然数相乘加 1，必定会等于一个平方数，
即 a(a + 1)(a + 2)(a + 3) + 1 = (a2 + 3a + 1)2。
(4)平方数必定不是完全数。
平方数必定是3的倍数或者3的倍数+1。
平方数必定是4的倍数或者4的倍数+1。
是否在相继正方形数之间存在一个素数，对9000000以内的数目是正确的。
(5) 中心正方形数的公式亦可表示成(
+ 1) / 2，n属于奇数
3.五边形数：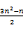
(1,5,12,22,35,…)
性质：
(1)奇奇偶偶
(2)第n个五边形数是第3n − 1个三角形数的1 / 3。首n个五边形数的算术平均数是第n个三角形数。
(3)依照费马多边形数定理，任何整数都可以表示为不超过5个五边形数的和。但大多数的整数都可以表示不超过3个五边形数的和。在小于106的整数中，只有以下6个整数需用5个五边形数的和来表示：9, 21, 31, 43, 55, 89
(4)广义五边形数，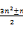
，n 依序为0, 1, -1, 2, -2, 3, -3, 4...
1)所有的整数都可以表示成不超过3个广义五边形数的和
2)若三角形数可以被3整除，则除以3之后的数必为广义五边形数
3)中心六边形数:较大的梯形可以表示为五边形数，而较小的梯形可以表示为广义五边形数
3n(n-1)+1=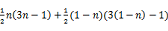
4.六边形数:n(2n-1)
任何大于1791的整数都能表达成最多4个六边形数之和。
5.七边形数：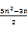
.
(1)七边形数的奇偶排列为奇-奇-偶-偶。如同平方数，七边形数在十进制下的数字根是 1, 4, 7, 9
(2)广义七边形数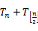
(3)每隔一个广义七边形数为一个正常的七边形数，如上面数列中的粗体字。除了1与70，没有一个广义七边形数也是沛尔数（Pell Numbers）
6.八边形数 3
-2n
(1)八边形数有不断的奇偶交替的性质。
(2)八边形数在十进位中的末位数以1 , 8, 1, 0, 5 , 6 , 3, 6 , 5 , 0的规律循环出现。
(3)根据费马多边形数定理，所有的整数都可以表示成至多8个八边形数的和。
7. 九边形数：
(1)7N(n)+3=T(7n+3)(N为九边形数，T为三角形数)
(2)奇—奇—偶—偶
8. 十边形数：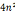
-3n
奇偶交替
9．十二边形数：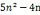
根据费马多边形数定理，所有的整数都可以表示成至多12个十二边形数的和。
奇偶交替
10. 四面体数（三角椎体数）n(n+1)(n+2)/6
(1)同时为四面体数和平方数的只有三个： 1, 4, 19600。
(2)同时是四面体数和四角锥数的只有1
(3)它们可以在杨辉三角每横行从右到左或左到右的第4项找到。（
）
11. 立方数（六面体数,六角锥数）n*n*n
(1)每个整数均可表示成9个或以下的正立方数之和。（华林问题）
(2)23和239须用9个正立方数。
(3) 只有15个整数需用8个
15, 22, 50, 114, 167, 175, 186, 212, 231, 238, 303, 364, 420, 428, 454
(4)的士数和士的数都指最小能表示成两个立方数之和的数，但的士数的必须为正数，士的数则无此限。
(5)只有一组连续三个立方数之和亦是立方数，就是3, 4, 5的立方，其和等于6的立方。
(6)在十进制，除了1之外，仅有4个的正整数其数字立方之和等同它本身，它们为153, 370, 371, 407
他们是n = 3的水仙花数。这4个三位数，亦可视为将它的数字分成三份，每份的立方之和，相似性质的整数有无限个，如165033, 221859, 336700等
12.八面体数 n(2
)/3
(1)八面体数 由两个四角锥叠起来, 另一个倒置在下面.
计算八面体数On可以用第n-1个和第n个四角锥数的和 , 或是使用公式:
(2)八面体数母函数
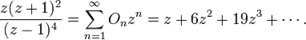
(3)波洛克爵士猜想在1850之内，每一个数字都可以写成最多7八面体数的总和
(4)八面体数On可以使用三角形数Tn表示
+ 4
= 
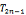
13.四角锥数（金字塔数，底面为正方形)。n(n+1)(2n+1)/6
(1)每层都是平方数合起来是正四角锥，也就是平方数的级数，平方数的和。
(2)也可表示成二项式系数的和:
Pn=
+
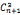
(3)两个四角锥数的总和是一个八面体数
14.五角锥数，
(1)第n个五角锥数等于前n个五角数的和。。
(2)第n个五角锥数为
与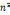
的平均数。第n个五角锥数同时等于第n个三角形数的n倍。
(3)五角锥数的母函数为
。
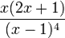15.五胞体数，
(1)辉三角第五行的开始，第n行的第n个数字就是五胞体数。
1, 5, 15, 35, 70, 126, 210, 330, 495, 715, 1001, 1365
(2)约有三分之二的五胞体数也是五角数。
第(3k − 2)个五胞体数始终是第((3k2 − k)/2)个五边形数
第(3k − 1)个五胞体数始终是第((3k2 + k)/2)个五边形数
第3k个五胞体数是广义的五边形数获得通过采取负指数−(3k2 + k)/2 在五边形数的公式. (这些表达式总是给整数).
16.星形数
(1)星数（六角星数或星形数或星状数） 6n(n - 1) + 1.
(2)从几何学上来看，星数(六角星数)是由中心一点和12个第(n-1)个三角形数组成 — 使数值等于中心十二边形数, 但是不完全相同.
(3)星数的数字根永远是1或4. 十进制的星数末两位只会出现下列数字 01, 13, 21, 33, 37, 41, 53, 61, 73, 81, 或 93.
(4)跳棋棋盘有121个棋位。
(5)星形数为平方数：
n=1:1
n=5:121
n=45
n=441
(6)星状质数是指同时是星数也是质数的数. 前几个星状质数是 13, 37, 73, 181, 337, 433, 541, 661, 937
17.五角星数:5n(n-1)+1
(1)五角星数也算是中心十边形数
18.七角星数7
− 7n + 1
(1)七角星数也算是中心十四边形数
19. 五边形数定理:欧拉函数的展开式如下：
(1)
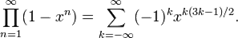
亦即
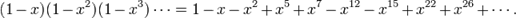
欧拉函数展开后，有些次方项被消去，只留下次方项为1, 2, 5, 7, 12, ...的项次，留下来的次方恰为广义五边形数。
(2)
和分割函数的关系
欧拉函数的倒数是分割函数的母函数，亦即：
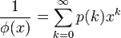
其中p ( k )为k的分割函数。
上式配合五边形数定理，可以得到
考虑x n项的系数，在n>0时，等式右侧的系数均为0，比较等式二侧的系数，可得
因此可得到分割函数p(n)的递归式
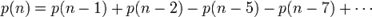
以n=10为例
p (10) = p (9) + p (8) − p (5) − p (3) = 30 + 22 − 7 − 3 = 42