Legend
Link ( extrm{to Codeforces})。
给定平面内的 (n) 个点,保证三点不共线。问存在多少个不同的“简单四边形-点”二元组,满足四边形内含这个点。
二元组不同当且仅当四边形或点不同,四边形不同当且仅当构成的点不同(即与连接顺序无关)。
(n le 2500)。
时空:( m{3s/1024MB})。
Editorial
枚举每一个点,统计有多少个四边形包含它?不好做,转换为有多少个四边形不包含它。
一个常见的套路是以当前统计点 ( m O) 为坐标原点对其它点进行极角排序。
排序后相当于计算多少个简单四边形不包含原点 ( m O)。这也有一个很套路的做法:
钦定一个点 ( m{B}) 是当前考察四边形的一个端点,连接直线 ( m{OB}),
则以 ( m{B}) 为起始端点的、不包含 ( m O) 的四边形上剩余三个点必然位于分割线 ( m{OB}) 同一侧。
如下图所示:
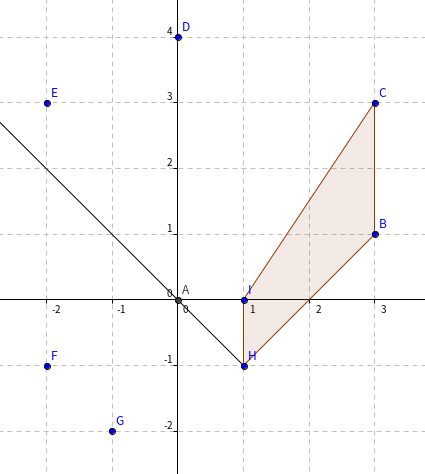
不难发现图中的 ( m H) 就是我们钦定的考察四边形的起始端点。
用组合数算算方案,只考虑直线的一侧就不会算重。
那么对于每一个点都如此计算以它为起始端点的四边形个数就可以了。
总复杂度是 (O(n^2 log n))。
doubt
你可能会质疑:这个做法对于凹四边形是否成立?那就对了,因为我开始想出这个做法的时候也对此有所怀疑。
但实际上凹四边形的情况也被正确考虑了。因为:
- 所有位于分割线同侧凹四边形按照上面的算法可以被正常排除;
- 其余的凹四边形一定会存在一种连接方式可以包含当前统计点。
Code
代码出乎意料地很短。
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int MX = 2500 + 3;
int n;
struct VECTOR{
LL x ,y;
VECTOR(LL _x = 0 ,LL _y = 0){x = _x ,y = _y;}
VECTOR operator -(const VECTOR& B)const{return VECTOR(x - B.x ,y - B.y);}
VECTOR operator +(const VECTOR& B)const{return VECTOR(x + B.x ,y + B.y);}
LL operator *(const VECTOR& B)const{return x * B.y - B.x * y;}
}P[MX] ,Q[MX];
int quadrant(VECTOR a){
if(a.x >= 0 && a.y >= 0) return 1;
if(a.x >= 0 && a.y <= 0) return 4;
if(a.x <= 0 && a.y >= 0) return 2;
if(a.x <= 0 && a.y <= 0) return 3;
assert(0);
return 0;
}
bool cmp(VECTOR a ,VECTOR b){
int q1 = quadrant(a) ,q2 = quadrant(b);
if(q1 != q2) return q1 < q2;
return (a * b) > 0;
}
LL C(LL n ,LL m){
if(m == 3) return n * (n - 1) * (n - 2) / 6;
if(m == 4) return n * (n - 1) * (n - 2) * (n - 3) / 24;
assert(0);
return 0;
}
LL calc(){
LL ret = 0;
int m = n - 1;
int l = 0;
// l 是最后一个合法的位置
for(int i = 0 ; i < m ; ++i){
while(Q[i] * Q[(l + 1) % m] > 0) l = (l + 1) % m;
ret += C((l - i + m) % m ,3);
}
return ret;
}
int main(){
cin >> n;
for(int i = 0 ,u ,v ; i < n ; ++i){
cin >> u >> v;
P[i] = VECTOR(u ,v);
}
LL Ans = C(n ,4) * (n - 4);
for(int i = 0 ; i < n ; ++i){
memcpy(Q ,P ,sizeof P);
VECTOR org = Q[i];
for(int j = 0 ; j < n ; ++j){
Q[j] = Q[j] - org;
}
std::swap(Q[i] ,Q[n - 1]);
std::sort(Q ,Q + n - 1 ,cmp);
Ans -= calc();
}
cout << Ans << endl;
return 0;
}