矩阵系列之一 ： 矩阵乘法的意义

一直想去深刻的了解一下矩阵，然而种种原因却将买回的书箱束之高阁。

今天看到了一个三元数的点（x,y,z）乘一个4x4的矩阵，好奇之下看了一下定义，较为复杂，却是不理解了，于是重新查了一下矩阵乘法的意义：

以下摘抄：

认为函数是有维度的。

可以将  看成是将  轴上的数据映射到了  轴上，这是一个从一维数轴的数据转换到另一个一维数轴上的对应关系。所以我认为这是一个一维函数。注意：这里将一维数轴看作和直角坐标轴有同等地位的一种坐标轴。

当然，  可以看成是将一个二维数据降成了一维，这里  表示一个二维数据，  表示一个一维数据。换句话说，这样的映射关系将一条二维信息转换为了一条一维信息，从几何角度说是，将一个平面“拍打“成了一条数轴。这个“拍打”（映射关系）我可以把它称之为“降维打击”。

我们再看一个比较有意思的，从二维到二维，这个时候你会发现，必须要用到两个函数即一个方程组才能描述出来

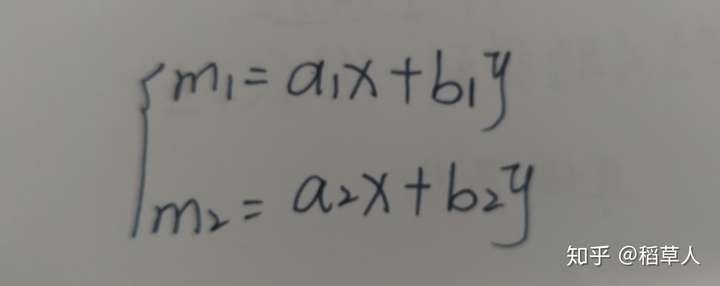
对于这个方程组，我们每给一个  ，都会收获一个  ，这是一个从二维数据到二维数据的过程，分析一下，会发现，其实  是通过第一个方程的映射关系将二维数据  下降成一维数据获得的，同样的，  是通过第二个方程的映射关系将同一个二维数据下降成一维获得的，然后将获得的两个一维数据组合成一个二维数据  .注意到，如果将  看成是直角坐标的一个点，那么  就是一个以  为横坐标， 以 为纵坐标的坐标系中的一个坐标。也就是讲：这个方程组的功能是将一个坐标系中的点转换到了另一个坐标系中的一个点。我们将这个方程组用矩阵的形式表达出来，也就是

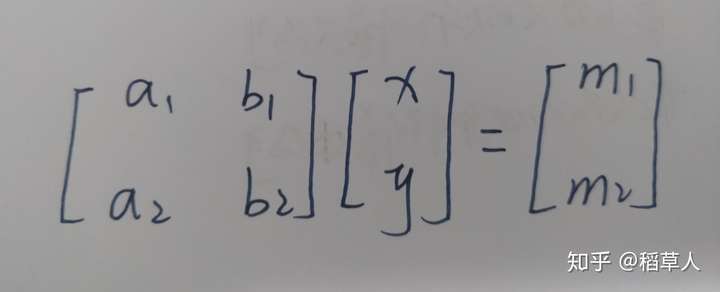
我们看着这个矩阵的形式，再重复一遍意思：将  ,  这个直角坐标系中的点  映射到了另一个以  为横坐标，  为纵坐标的坐标系中去了。

我们将直角坐标系中的点具象化

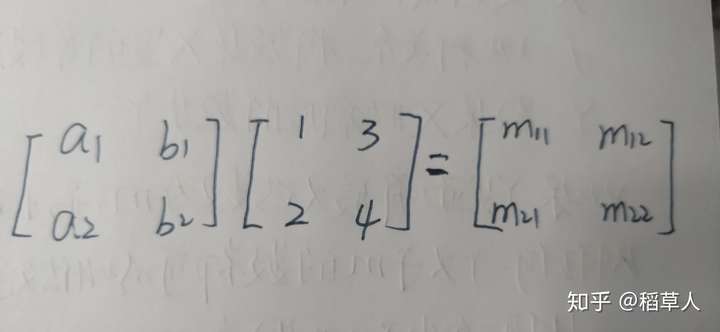
这个矩阵形式表示什么意思呢？

显然，通过上面的讨论，这表示将直角坐标系中的点  和  映射到了以  为横坐标，以  为纵坐标的坐标系中去了，得到对应的两个点  和  .

进一步对矩阵形式具象化

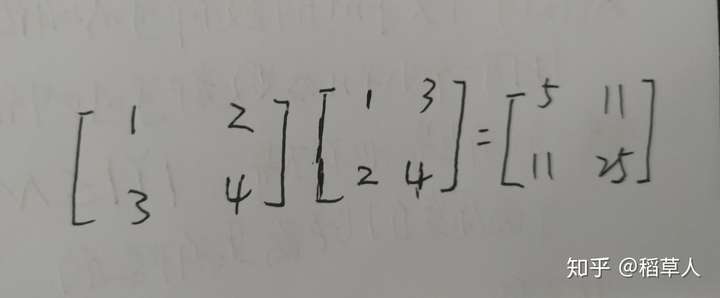
这个矩阵形式表示什么意思呢？

显然，这表示将直角坐标系中的点  和  映射到了以  为横坐标，以  为纵坐标的坐标系中去啦，得到对应的两个点  和  .

再看一个例子

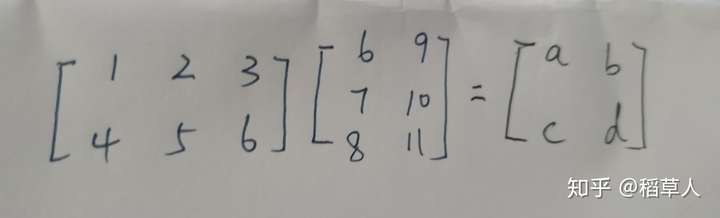
这表示什么意思呢，显然是将  和  从三维坐标系  映射到二维坐标系  ，  中去，得到  两点。注意，这已经将两个三维数据降维到两个二维数据了！！！

综上你会发现矩阵相乘的几何意义：将一个坐标系中所有的点映射到另一个坐标系中去。

当然，更为抽象的说法是，坐标系变换（即将一个坐标系变换成另一个坐标系，从一个空间转换到另一个空间）。

看完虽然不足以理解最初看到的疑问，但充分理解了一般矩阵乘法的意义！