目标：
- 构建具有单隐藏层的2类分类神经网络。
- 使用具有非线性激活功能激活函数，例如tanh。
- 计算交叉熵损失（损失函数）。
- 实现向前和向后传播。
一、准备软件包
- numpy：是用Python进行科学计算的基本软件包。
- sklearn：为数据挖掘和数据分析提供的简单高效的工具。
- matplotlib ：是一个用于在Python中绘制图表的库。
- testCases：提供了一些测试示例来评估函数的正确性，参见下载的资料或者在底部查看它的代码。
- planar_utils ：提供了在这个任务中使用的各种有用的功能，参见下载的资料或者在底部查看它的代码。
import numpy as np import matplotlib.pyplot as plt from testCases import * import sklearn import sklearn.datasets from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets %matplotlib inline np.random.seed(1)##设置一个固定的随机种子，以保证接下来的步骤中我们的结果是一致的。
二、加载和查看数据集
#加载数据集 X,Y = load_planar_dataset()#将一个花的图案的2类数据集加载到变量X和Y #查看数据集 plt.scatter(X[0,:],X[1,:],c=np.squeeze(Y),s = 20,cmap = plt.cm.Spectral)
plt.scatter用法参考https://www.jb51.net/article/127806.htm
运行结果：
数据看起来像一朵红色（y = 0）和一些蓝色（y = 1）的数据点的花朵的图案。 我们的目标是建立一个模型来适应这些数据。现在，我们已经有了以下的东西：
- X：一个numpy的矩阵，包含了这些数据点的数值
- Y：一个numpy的向量，对应着的是X的标签【0 | 1】（红色:0 ， 蓝色 :1）
我们继续来仔细地看数据（查看维度）：
#查看维度 shape_X = X.shape shape_Y = Y.shape m = Y.shape[1]#训练集里面的数量 print("X的维度为："+str(shape_X)) print("Y的维度为："+str(shape_Y)) print("数据集里面的数据有："+str(m)+"个")
运行结果：
三、查看简单的Logistic回归的分类效果
在构建完整的神经网络之前，先让我们看看逻辑回归在这个问题上的表现如何，我们可以使用sklearn的内置函数来做到这一点， 运行下面的代码来训练数据集上的逻辑回归分类器。
#使用Logistic回归测试效果 clf = sklearn.linear_model.LogisticRegressionCV() clf.fit(X.T,Y.T)#建立逻辑回归分类器
运行结果（不同的机器提示大同小异）：
我们可以把逻辑回归分类器的分类绘制出来：
#逻辑回归分类器的分类绘制 plot_decision_boundary(lambda x: clf.predict(x), X, Y) #绘制决策边界 plt.title("Logistic Regression") #图标题 LR_predictions = clf.predict(X.T) #预测结果 print ("逻辑回归的准确性： %d " % float((np.dot(Y, LR_predictions) + np.dot(1 - Y,1 - LR_predictions)) / float(Y.size) * 100) + "% " + "(正确标记的数据点所占的百分比)"
运行结果：
准确性只有47%的原因是数据集不是线性可分的，所以逻辑回归表现不佳，现在我们正式开始构建神经网络。
四、搭建神经网络
我们要搭建的神经网络模型如下图：
当然还有我们的理论基础：
对于
而言：
构建神经网络的一般方法是：
1、定义神经网络结构（输入单元的数量，隐藏单元的数量等）。
2、初始化模型的参数
3、循环：
- 实施前向传播
- 计算损失
- 实现向后传播
- 更新参数（梯度下降）
我们要它们合并到一个nn_model() 函数中，当我们构建好了nn_model()并学习了正确的参数，我们就可以预测新的数据。
（一）定义神经网络结构
在构建之前，我们要先把神经网络的结构给定义好：
- n_x: 输入层的数量
- n_h: 隐藏层的数量（这里设置为4）
- n_y: 输出层的数量
代码如下：
''' 搭建神经网络 1、定义神经网络结构（输入单元的数量，隐藏单元的数量等）。 2、初始化模型的参数 3、循环： 实施前向传播 计算损失 实现向后传播 更新参数（梯度下降） ''' #定义神经网络结构 def layer_sizes(X,Y): """ 参数： X - 输入数据集,维度为（输入的数量，训练/测试的数量） Y - 标签，维度为（输出的数量，训练/测试数量） 返回： n_x - 输入层的数量 n_h - 隐藏层的数量 n_y - 输出层的数量 """ n_x = X.shape[0]#输入层 n_h = 4 #隐藏层，硬编码为4 n_y = Y.shape[0]#输出层 return(n_x,n_h,n_y)
测试layer_sizes
#测试layer_sizes print("=====================测试layer_sizes====================") X_asses , Y_asses = layer_sizes_test_case() (n_x,n_h,n_y) = layer_sizes(X_asses,Y_asses) print("输入层的节点数量为: n_x = " + str(n_x)) print("隐藏层的节点数量为: n_h = " + str(n_h)) print("输出层的节点数量为: n_y = " + str(n_y))
运行结果：
（二）初始化模型参数
首先，我们了解一下断言：https://www.cnblogs.com/hzzhbest/p/15153232.html
代码如下：
def initialize_parameters( n_x , n_h ,n_y): """ 参数： n_x - 输入层节点的数量 n_h - 隐藏层节点的数量 n_y - 输出层节点的数量 返回： parameters - 包含参数的字典： W1 - 权重矩阵,维度为（n_h，n_x） b1 - 偏向量，维度为（n_h，1） W2 - 权重矩阵，维度为（n_y，n_h） b2 - 偏向量，维度为（n_y，1） """ np.random.seed(2) #指定一个随机种子，以便你的输出与我们的一样。 W1 = np.random.randn(n_h,n_x) * 0.01 b1 = np.zeros(shape=(n_h, 1)) W2 = np.random.randn(n_y,n_h) * 0.01 b2 = np.zeros(shape=(n_y, 1)) #使用断言确保我的数据格式是正确的 assert(W1.shape == ( n_h , n_x )) assert(b1.shape == ( n_h , 1 )) assert(W2.shape == ( n_y , n_h )) assert(b2.shape == ( n_y , 1 )) parameters = {"W1" : W1, "b1" : b1, "W2" : W2, "b2" : b2 } return parameters
说明：
（1）随机值初始化权重矩阵：np.random.randn(a，b)* 0.01来随机初始化一个维度为(a，b)的矩阵。
（2）将偏向量初始化为零：np.zeros((a，b))用零初始化矩阵（a，b）。
测试初始化模型：
#测试initialize_parameters print("=========================测试initialize_parameters=========================") n_x , n_h , n_y = initialize_parameters_test_case() parameters = initialize_parameters(n_x , n_h , n_y) print("W1 = " + str(parameters["W1"])) print("b1 = " + str(parameters["b1"])) print("W2 = " + str(parameters["W2"])) print("b2 = " + str(parameters["b2"]))
运行结果：
（三）循环向前传播
我们可以使用sigmoid()函数，也可以使用np.tanh()函数。步骤如下：
代码如下：
#向前传播 def forward_propagation( X , parameters ): """ 参数： X - 维度为（n_x，m）的输入数据。 parameters - 初始化函数（initialize_parameters）的输出 返回： A2 - 使用sigmoid()函数计算的第二次激活后的数值 cache - 包含“Z1”，“A1”，“Z2”和“A2”的字典类型变量 """ W1 = parameters["W1"] b1 = parameters["b1"] W2 = parameters["W2"] b2 = parameters["b2"] #前向传播计算A2 Z1 = np.dot(W1 , X) + b1 A1 = np.tanh(Z1) Z2 = np.dot(W2 , A1) + b2 A2 = sigmoid(Z2) #使用断言确保我的数据格式是正确的 assert(A2.shape == (1,X.shape[1])) cache = {"Z1": Z1, "A1": A1, "Z2": Z2, "A2": A2} return (A2, cache)
测试向前传播：
#测试forward_propagation print("=========================测试forward_propagation=========================") X_assess, parameters = forward_propagation_test_case() A2, cache = forward_propagation(X_assess, parameters) print(np.mean(cache["Z1"]), np.mean(cache["A1"]), np.mean(cache["Z2"]), np.mean(cache["A2"]))
运行结果：
现在我们已经计算了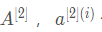
包含了训练集里每个数值，现在我们就可以构建成本函数了。
（四）计算损失
计算成本的公式如下：
有很多的方法都可以计算交叉熵损失，比如下面的这个公式，我们在python中可以这么实现：
logprobs = np.multiply(np.log(A2),Y) cost = - np.sum(logprobs) # 不需要使用循环就可以直接算出来。
当然，你也可以使用np.multiply（）然后使用np.sum（）或者直接使用np.dot（）
现在我们正式开始构建计算成本的函数：
#计算损失 def compute_cost(A2,Y,parameters): """ 计算方程（6）中给出的交叉熵成本， 参数： A2 - 使用sigmoid()函数计算的第二次激活后的数值 Y - "True"标签向量,维度为（1，数量） parameters - 一个包含W1，B1，W2和B2的字典类型的变量 返回： 成本 - 交叉熵成本给出方程（13） """ m = Y.shape[1] W1 = parameters["W1"] W2 = parameters["W2"] #计算成本 logprobs = logprobs = np.multiply(np.log(A2), Y) + np.multiply((1 - Y), np.log(1 - A2)) cost = - np.sum(logprobs) / m cost = float(np.squeeze(cost)) assert(isinstance(cost,float)) return cost
测试成本函数：
#测试compute_cost print("=========================测试compute_cost=========================") A2 , Y_assess , parameters = compute_cost_test_case() print("cost = " + str(compute_cost(A2,Y_assess,parameters)))
运行结果：
（五）向后传播
方程如下：
代码如下：
#反向传播 def backward_propagation(parameters,cache,X,Y): """ 使用上述说明搭建反向传播函数。 参数： parameters - 包含我们的参数的一个字典类型的变量。 cache - 包含“Z1”，“A1”，“Z2”和“A2”的字典类型的变量。 X - 输入数据，维度为（2，数量） Y - “True”标签，维度为（1，数量） 返回： grads - 包含W和b的导数一个字典类型的变量。 """ m = X.shape[1] W1 = parameters["W1"] W2 = parameters["W2"] A1 = cache["A1"] A2 = cache["A2"] dZ2= A2 - Y dW2 = (1 / m) * np.dot(dZ2, A1.T) db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True) dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2)) dW1 = (1 / m) * np.dot(dZ1, X.T) db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True) grads = {"dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2 } return grads
测试反向传播：
#测试backward_propagation print("=========================测试backward_propagation=========================") parameters, cache, X_assess, Y_assess = backward_propagation_test_case() grads = backward_propagation(parameters, cache, X_assess, Y_assess) print ("dW1 = "+ str(grads["dW1"])) print ("db1 = "+ str(grads["db1"])) print ("dW2 = "+ str(grads["dW2"])) print ("db2 = "+ str(grads["db2"]))
运行结果：
(六）更新参数
我们需要使用(dW1, db1, dW2, db2)来更新(W1, b1, W2, b2)。
更新算法如下：
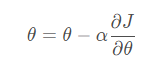
- α：学习速率
- θ：参数
我们需要选择一个良好的学习速率，我们可以看一下下面这两个图(由Adam Harley提供)：
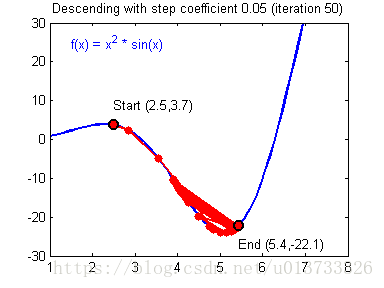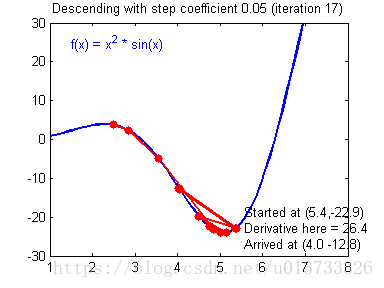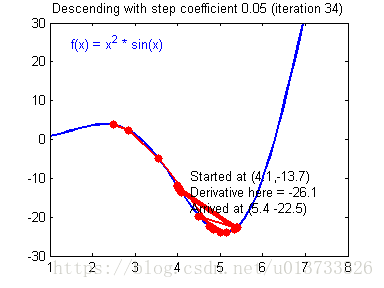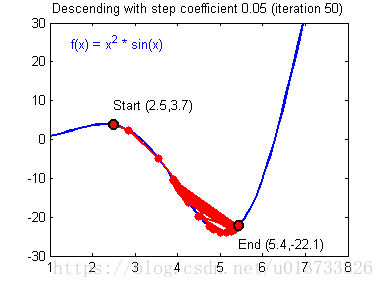
上面两个图分别代表了具有良好学习速率（收敛）和不良学习速率（发散）的梯度下降算法。
代码如下：
#更新参数（梯度下降） def update_parameters(parameters,grads,learning_rate=1.2): """ 使用上面给出的梯度下降更新规则更新参数 参数： parameters - 包含参数的字典类型的变量。 grads - 包含导数值的字典类型的变量。 learning_rate - 学习速率 返回： parameters - 包含更新参数的字典类型的变量。 """ W1,W2 = parameters["W1"],parameters["W2"] b1,b2 = parameters["b1"],parameters["b2"] dW1,dW2 = grads["dW1"],grads["dW2"] db1,db2 = grads["db1"],grads["db2"] W1 = W1 - learning_rate * dW1 b1 = b1 - learning_rate * db1 W2 = W2 - learning_rate * dW2 b2 = b2 - learning_rate * db2 parameters = {"W1": W1, "b1": b1, "W2": W2, "b2": b2} return parameters
测试：
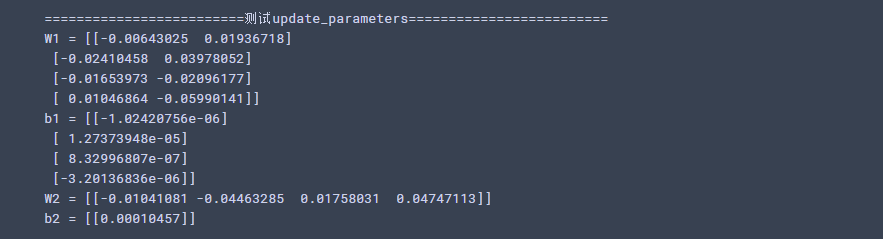
#测试update_parameters print("=========================测试update_parameters=========================") parameters, grads = update_parameters_test_case() parameters = update_parameters(parameters, grads) print("W1 = " + str(parameters["W1"])) print("b1 = " + str(parameters["b1"])) print("W2 = " + str(parameters["W2"])) print("b2 = " + str(parameters["b2"]))
运行结果：
（七）整合
我们现在把上面的东西整合到nn_model()中，神经网络模型必须以正确的顺序使用先前的功能。
#整合 def nn_model(X,Y,n_h,num_iterations,print_cost=False): """ 参数： X - 数据集,维度为（2，示例数） Y - 标签，维度为（1，示例数） n_h - 隐藏层的数量 num_iterations - 梯度下降循环中的迭代次数 print_cost - 如果为True，则每1000次迭代打印一次成本数值 返回： parameters - 模型学习的参数，它们可以用来进行预测。 """ np.random.seed(3) #指定随机种子 n_x = layer_sizes(X, Y)[0] n_y = layer_sizes(X, Y)[2] parameters = initialize_parameters(n_x,n_h,n_y) W1 = parameters["W1"] b1 = parameters["b1"] W2 = parameters["W2"] b2 = parameters["b2"] for i in range(num_iterations): A2 , cache = forward_propagation(X,parameters) cost = compute_cost(A2,Y,parameters) grads = backward_propagation(parameters,cache,X,Y) parameters = update_parameters(parameters,grads,learning_rate = 0.5) if print_cost: if i%1000 == 0: print("第 ",i," 次循环，成本为："+str(cost)) return parameters
测试模块：
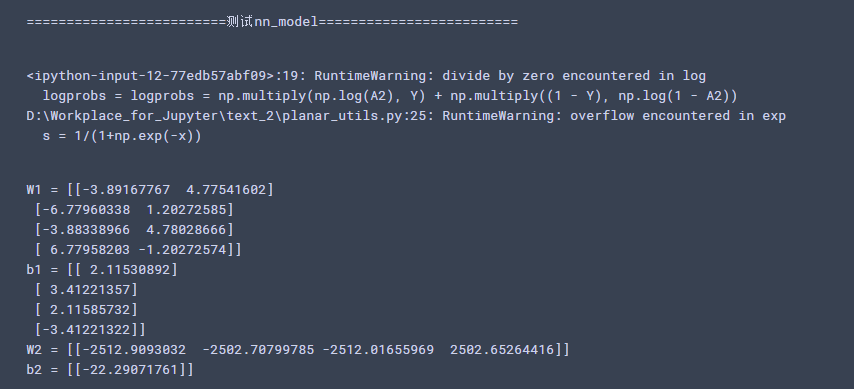
#测试nn_model print("=========================测试nn_model=========================") X_assess, Y_assess = nn_model_test_case() parameters = nn_model(X_assess, Y_assess, 4, num_iterations=10000, print_cost=False) print("W1 = " + str(parameters["W1"])) print("b1 = " + str(parameters["b1"])) print("W2 = " + str(parameters["W2"])) print("b2 = " + str(parameters["b2"]))
运行结果：
（八）预测
构建predict()来使用模型进行预测， 使用向前传播来预测结果。
#预测 def predict(parameters,X): """ 使用学习的参数，为X中的每个示例预测一个类 参数： parameters - 包含参数的字典类型的变量。 X - 输入数据（n_x，m） 返回 predictions - 我们模型预测的向量（红色：0 /蓝色：1） """ A2 , cache = forward_propagation(X,parameters) predictions = np.round(A2) return predictions
测试预测：
#测试predict print("=========================测试predict=========================") parameters, X_assess = predict_test_case() predictions = predict(parameters, X_assess) print("预测的平均值 = " + str(np.mean(predictions)))
运行结果：
（九）正式运行
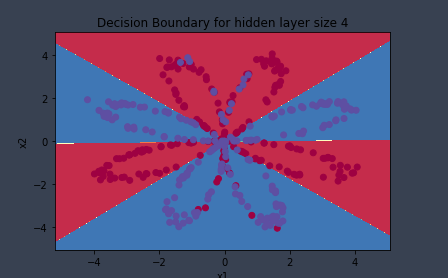
#正式运行 parameters = nn_model(X, Y, n_h = 4, num_iterations=50000, print_cost=True) #绘制边界 plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y) plt.title("Decision Boundary for hidden layer size " + str(4)) predictions = predict(parameters, X) print ('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
运行结果：
第 0 次循环，成本为：0.6930480201239823 第 1000 次循环，成本为：0.3098018601352803 第 2000 次循环，成本为：0.2924326333792646 第 3000 次循环，成本为：0.2833492852647412 第 4000 次循环，成本为：0.27678077562979253 第 5000 次循环，成本为：0.26347155088593144 第 6000 次循环，成本为：0.24204413129940763 第 7000 次循环，成本为：0.23552486626608762 第 8000 次循环，成本为：0.23140964509854278 第 9000 次循环，成本为：0.22846408048352365 第 10000 次循环，成本为：0.22618596442552621 第 11000 次循环，成本为：0.22433396831991878 第 12000 次循环，成本为：0.22277683894021222 第 13000 次循环，成本为：0.22143562034302341 第 14000 次循环，成本为：0.22025881798488608 第 15000 次循环，成本为：0.219211255282511 第 16000 次循环，成本为：0.21826898800675665 第 17000 次循环，成本为：0.21741576507251686 第 18000 次循环，成本为：0.21663975930881296 第 19000 次循环，成本为：0.2159315388239913 第 20000 次循环，成本为：0.21528318622387338 第 21000 次循环，成本为：0.21468791890292035 第 22000 次循环，成本为：0.21413987810119145 第 23000 次循环，成本为：0.2136339800015628 第 24000 次循环，成本为：0.2131657976873604 第 25000 次循环，成本为：0.21273146371264928 第 26000 次循环，成本为：0.21232758870309454 第 27000 次循环，成本为：0.2119511930830476 第 28000 次循环，成本为：0.2115996496847822 第 29000 次循环，成本为：0.21127063539172294 第 30000 次循环，成本为：0.21096209027852467 第 31000 次循环，成本为：0.2106721829748801 第 32000 次循环，成本为：0.2103992812042238 第 33000 次循环，成本为：0.2101419266361328 第 34000 次循环，成本为：0.20989881334599658 第 35000 次循环，成本为：0.20966876930197412 第 36000 次循环，成本为：0.20945074040200518 第 37000 次循环，成本为：0.20924377666697203 第 38000 次循环，成本为：0.20904702026369804 第 39000 次循环，成本为：0.2088596950864057 第 40000 次循环，成本为：0.20868109767003282 第 41000 次循环，成本为：0.20851058924544028 第 42000 次循环，成本为：0.2083475887766385 第 43000 次循环，成本为：0.20819156684497542 第 44000 次循环，成本为：0.20804204026579343 第 45000 次循环，成本为：0.20789856734016154 第 46000 次循环，成本为：0.20776074365857347 第 47000 次循环，成本为：0.20762819838547728 第 48000 次循环，成本为：0.20750059096357965 第 49000 次循环，成本为：0.2073776081853776 准确率: 91%
（十）更改隐藏层节点数量
我们上面的实验把隐藏层定为4个节点，现在我们更改隐藏层里面的节点数量，看一看节点数量是否会对结果造成影响。
#更改隐藏层里面的节点数量 plt.figure(figsize=(16, 32)) hidden_layer_sizes = [1, 2, 3, 4, 5,20, 50] #隐藏层数量 for i, n_h in enumerate(hidden_layer_sizes): plt.subplot(5, 2, i + 1) plt.title('Hidden Layer of size %d' % n_h) parameters = nn_model(X, Y, n_h, num_iterations=10000) plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y) predictions = predict(parameters, X) accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) print ("隐藏层的节点数量： {} ，准确率: {} %".format(n_h, accuracy))
运行结果：
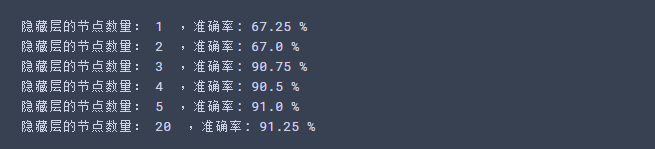
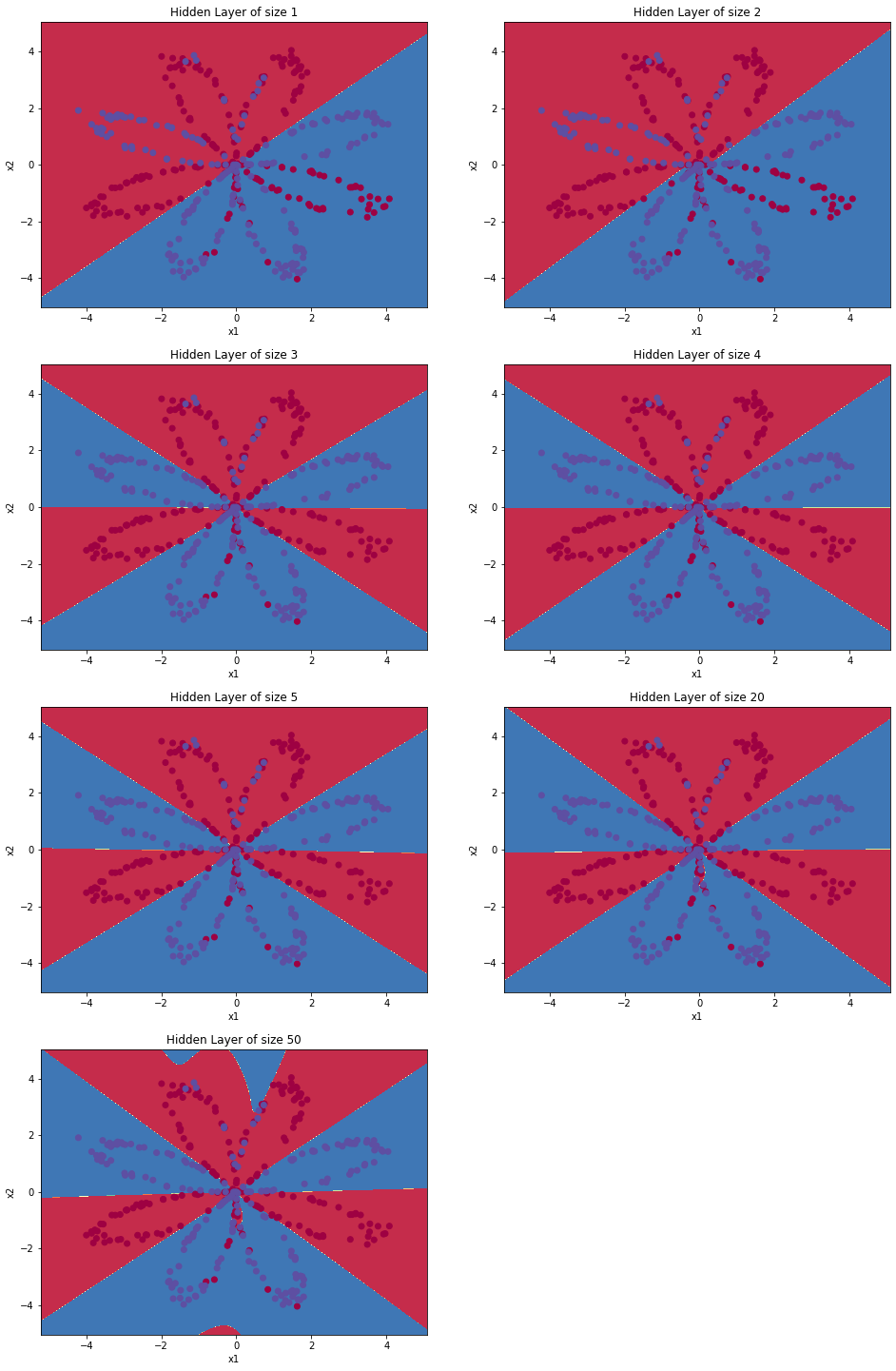
较大的模型（具有更多隐藏单元）能够更好地适应训练集，直到最终的最大模型过度拟合数据。
最好的隐藏层大小似乎在n_h = 5附近。实际上，这里的值似乎很适合数据，而且不会引起过度拟合。
正则化允许我们使用非常大的模型（如n_h = 50），而不会出现太多过度拟合。
参考：https://blog.csdn.net/weixin_36815313/article/details/105342898