符号说明
a|b a整除b
(a,b) a与b的最大公因数
[a,b] a与b的最小公倍数
pα||a pα|a但pα+1∤a
a≡b(mod m) a与b对模m同余
a-1 (mod m) a对模m的数论倒数
性质1 如果a|b,那么(-a)|b,反过来也成立
性质2 如果a|b,b|c,那么a|c
性质3 如果a|b,a|c,那么对任意整数x,y都有 a|(bx+cy)
性质4 设n为大于1的正整数,p是n的大于1的因数中最小的正整数,则p为素数
性质5 素数中有且只有一个偶数2
贝祖定理 设d=(a,b) 则存在整数x,y 使得 ax+by=d
若a,b是整数,方程ax+by=d有整数解当且仅(a,b)|d
性质6 设d为a,b的公因数 则d|(a,b)
性质7 设a|c,b|c 且 (a,b)=1 则 ab|c
性质8 设p为素数,p|ab,则p|a或p|b
性质9 设a,b都是正整数 则[a,b]*(a,b)=ab
记F[n]为斐波那契数列第n项 有 (F[a],F[b])=F[(a,b)]
算数基本定理 
又称质因数分解 code:

// 质因数分解 O(√) int facorize(int x, int* p) { int cnt = 0; for (int i = 2; i * i <= x; i++) { while (x % i == 0) { p[cnt++] = i; x /= i; } } if (x > 1) p[cnt++] = x; //如果x>1,则说明剩下的x是素数,也要放进数组 return cnt; }
拓展欧几里得算法

int exgcd(int a, int b, int& x, int& y) { if (b == 0) { x = 1; y = 0; return a; } int g = exgcd(b, a % b, x, y); int t = x; x = y; y = t - a / b * y; return g; }
性质10
如果a1≡ b1 (mod m)
a2≡ b2 (mod m)
那么 a1±a2 ≡ b1± b2 (mod m)
a1a2 ≡ b1b2 (mod m)
性质11 a≡b (mod m) 的充要条件是 m|a-b
性质12 若a≡b(mod m) ,n为正整数,则an≡bn (mod m)
Fermat小定理 设p为素数,a为整数,则ap≡a(mod p). 特别地,若p∤a,则ap-1≡1(mod p)
欧拉函数 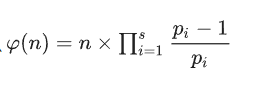
1~n中所有数的欧拉phi函数值 O(nloglongn)

void phi_table(int n, int* phi) { for (int i = 2; i <= n; i++) phi[i] = 0; phi[1] = 1; for (int i = 2; i <= n; i++) if (!phi[i]) for (int j = i; j <= n; j += i) { if (!phi[j]) phi[j] = j; phi[j] = phi[j] / i * (i - 1); } }
求单个数的欧拉函数 0(√n)

int euler_phi(int n) { int m = int(sqrt(n + 0.5)); int ans = n; for (int i = 2; i <= m; i++) { if (n % i == 0) { ans = ans / i * (i - 1); while (n % i == 0) n /= i; } } if (n > 1) ans = ans / n * (n - 1); return ans; }
线性求逆元 0(n)
对于求一连串数字对于p的逆元,只能用这种方法,别的方法都比这个慢

int inv[105]; void inver(int p) { inv[1] = 1; for (int i = 2; i < p; i++) { inv[i] = (p - p / i) * inv[p % i] % p; } }
当p为素数,且ap互质时可以用快速幂求逆元
x=QuickPower(a,p-2,p);
当p不为素数时,可以用拓展欧几里得算法求逆元

int main() { ll x, y; exgcd(a, p, x, y); x = (x % p + p) % p; //x是 a 在mod p下的逆元 return 0; }
