2132: 圈地计划
Time Limit: 2 Sec Memory Limit: 256 MB
Submit: 1675 Solved: 782
[Submit][Status][Discuss]
Description
最近房地产商GDOI(Group of Dumbbells Or Idiots)从NOI(Nuts Old Idiots)手中得到了一块开发土地。据了解,
这块土地是一块矩形的区域,可以纵横划分为N×M块小区域。GDOI要求将这些区域分为商业区和工业区来开发。根
据不同的地形环境,每块小区域建造商业区和工业区能取得不同的经济价值。更具体点,对于第i行第j列的区域,
建造商业区将得到Aij收益,建造工业区将得到Bij收益。另外不同的区域连在一起可以得到额外的收益,即如果区
域(I,j)相邻(相邻是指两个格子有公共边)有K块(显然K不超过4)类型不同于(I,j)的区域,则这块区域能增加k
×Cij收益。经过Tiger.S教授的勘察,收益矩阵A,B,C都已经知道了。你能帮GDOI求出一个收益最大的方案么?
Input
输入第一行为两个整数,分别为正整数N和M,分别表示区域的行数和列数;
第2到N+1列,每行M个整数,表示商业区收益矩阵A;
第N+2到2N+1列,每行M个整数,表示工业区收益矩阵B;
第2N+2到3N+1行,每行M个整数,表示相邻额外收益矩阵C。
任何数字不超过1000”的限制
Output
输出只有一行,包含一个整数,为最大收益值。
Sample Input
3 3
1 2 3
4 5 6
7 8 9
9 8 7
6 5 4
3 2 1
1 1 1
1 3 1
1 1 1
Sample Output
81
【数据规模】
对于100%的数据有N,M≤100
HINT
数据已加强,并重测--2015.5.15
题解
最小割。如果相邻割相同的话,不(呵)难(呵)想出建模:
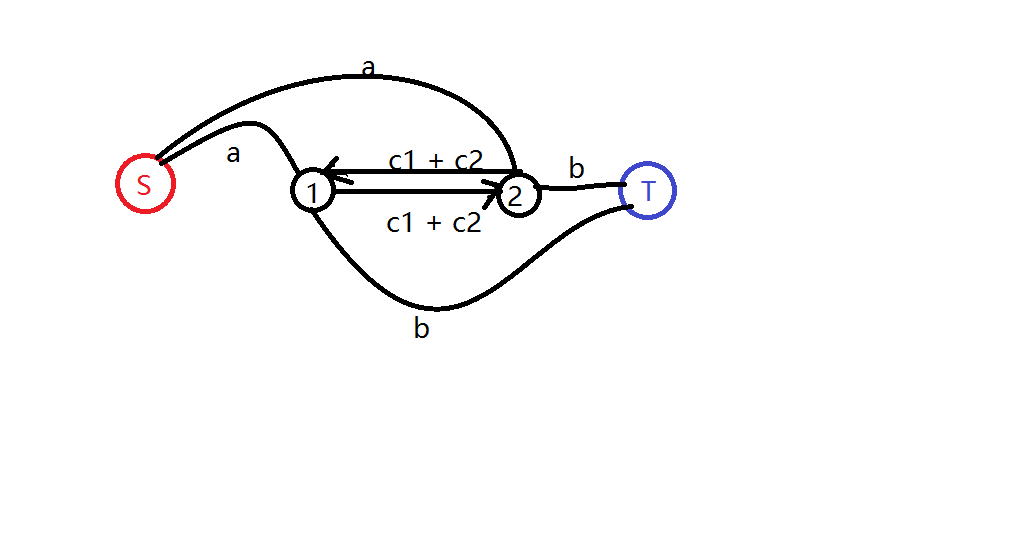
考虑均选a、均选b、1a2b、1b2a情况下的答案,或者考虑每条路径的含义,对于某条路径割掉某条边的含义
发现答案为a + a + b + b + c1 + c2 - 最小割
但是如果相邻割要求不同才能有价值,那么中间的c1 + c2应为-c1 - c2,显然不能有负容量。
怎么办?
换!
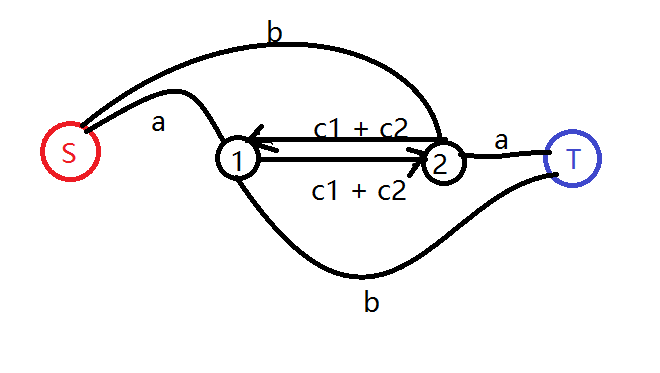
考虑均选a、均选b、1a2b、1b2a情况下的答案,或者考虑每条路径的含义,对于某条路径割掉某条边的含义
答案为a + a + b + b + c1 + c2 - 最小割
如此建图即可
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <map>
#include <cmath>
inline int max(int a, int b){return a > b ? a : b;}
inline int min(int a, int b){return a < b ? a : b;}
inline int abs(int x){return x < 0 ? -x : x;}
inline void swap(int &x, int &y){int tmp = x;x = y;y = tmp;}
inline void read(int &x)
{
x = 0;char ch = getchar(), c = ch;
while(ch < '0' || ch > '9') c = ch, ch = getchar();
while(ch <= '9' && ch >= '0') x = x * 10 + ch - '0', ch = getchar();
if(c == '-') x = -x;
}
const int INF = 0x3f3f3f3f;
const int dx[4] = {1, -1, 0, 0};
const int dy[4] = {0, 0, 1, -1};
struct Edge
{
int u,v,w,nxt;
Edge(int _u, int _v, int _w, int _nxt){u = _u;v = _v;w = _w;nxt = _nxt;}
Edge(){}
}edge[1000010];
int head[100010], cnt = 1, S, T, q[100010], he, ta, h[100010], ans;
inline void insert(int a, int b, int c)
{
edge[++ cnt] = Edge(a, b, c, head[a]), head[a] = cnt;
edge[++ cnt] = Edge(b, a, 0, head[b]), head[b] = cnt;
}
bool bfs()
{
memset(h, -1, sizeof(h)), h[S] = 0, he = ta = 0, q[ta ++] = S;
while(he < ta)
{
int now = q[he ++];
for(int pos = head[now];pos;pos = edge[pos].nxt)
{
int v = edge[pos].v;
if(edge[pos].w && h[v] == -1)
h[v] = h[now] + 1, q[ta ++] = v;
}
}
return h[T] != -1;
}
int dfs(int x, int f)
{
if(x == T) return f;
int used = 0, w;
for(int pos = head[x];pos;pos = edge[pos].nxt)
{
int v = edge[pos].v;
if(h[v] == h[x] + 1)
{
w = dfs(v, min(edge[pos].w, f - used));
edge[pos].w -= w;
edge[pos ^ 1].w += w;
used += w;
if(used == f) return f;
}
}
if(!used) h[x] = -1;
return used;
}
void dinic()
{
while(bfs()) ans += dfs(S, INF);
}
int n,m,a[1010][1010],b[1010][1010],c[1010][1010],num[1010][1010], tot, sum;
int main()
{
read(n), read(m);
for(int i = 1;i <= n;++ i)
for(int j = 1;j <= m;++ j)
num[i][j] = ++ tot;
S = tot + 1, T = S + 1;
for(int i = 1;i <= n;++ i)
for(int j = 1;j <= m;++ j)
{
read(a[i][j]);
if((i + j) & 1)
insert(S, num[i][j], a[i][j]), sum += a[i][j];
}
for(int i = 1;i <= n;++ i)
for(int j = 1;j <= m;++ j)
{
read(b[i][j]);
if((i + j) & 1) insert(num[i][j], T, b[i][j]), sum += b[i][j];
else insert(S, num[i][j], b[i][j]), insert(num[i][j], T, a[i][j]), sum += a[i][j], sum += b[i][j];
}
for(int i = 1;i <= n;++ i)
for(int j = 1;j <= m;++ j)
read(c[i][j]);
for(int i = 1;i <= n;++ i)
for(int j = 1;j <= m;++ j)
if((i + j) & 1)
for(int k = 0;k < 4;++ k)
{
int xx = i + dx[k], yy = j + dy[k];
if(xx <= 0 || yy <= 0 || xx > n || yy > m) continue;
insert(num[i][j], num[xx][yy], c[i][j] + c[xx][yy]);
insert(num[xx][yy], num[i][j], c[i][j] + c[xx][yy]);
sum += c[i][j] + c[xx][yy];
}
dinic();
printf("%d", sum - ans);
return 0;
}