剑指offer：斐波那契数列，跳台阶，变态跳台阶—

剑指offer：斐波那契数列，跳台阶，变态跳台阶——斐波那契数列类题目：

在做题过程中接触到一类比较像的问题，我认为都可以由斐波那契数列归类出来，它们的解决都是依靠之前步骤有序推得的，比较经典的解法是递归，但是递归的话时间复杂度和空间复杂度不好，我们画一个斐波那契数列递归求法的图就可以知道：

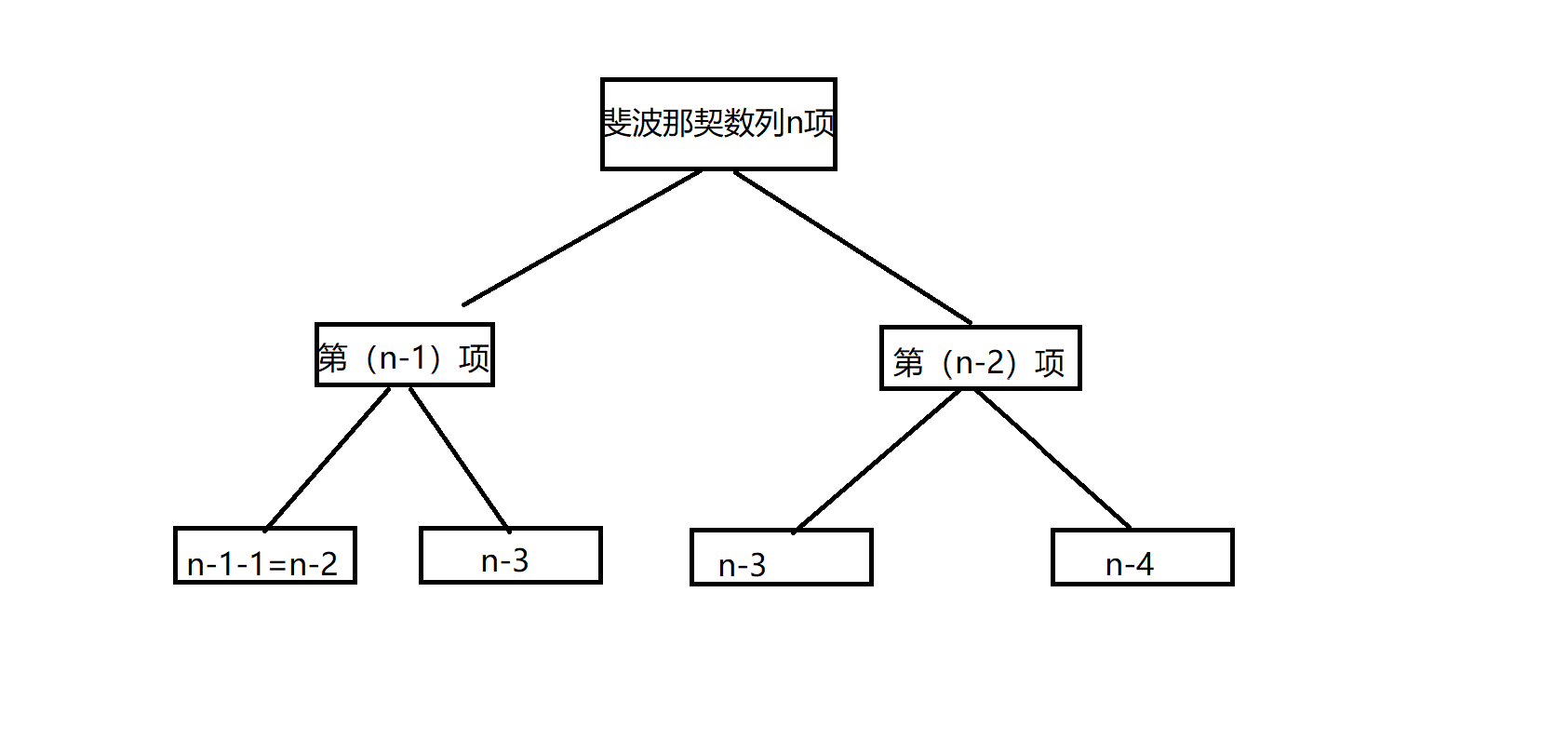
可以看到有许多项是重复的，如果用递归的话许多无所谓的分支较为耗时间耗空间，所以反而不如用常规的正向生成的思维，这样前面生成的项可以直接拿来用于计算后面的项，重用性比较高，空间利用率也就上去了。

题目1：大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0，第1项是1）。

# -*- coding:utf-8 -*-
class Solution:
    def Fibonacci(self, n):
        # write code here
        t1=0
        t2=1
        if n==0:
            return 0
        elif n==1:
            return 1
        for i in range(1,n):
            temp=t2
            t2=t1+t2 
            t1=temp
        return t2

与这道题非常像的就是青蛙跳台阶问题，读题后我们发现，青蛙跳台阶可以跳1，也可以跳2，那么每次拿到一个n，求跳法，就有两种思路，青蛙刚开始跳1，后面要解决的问题就是青蛙跳n-1的情况；而青蛙刚开始跳2，后面要解决的问题就是青蛙跳n-2的情况，这时我们可能非常开心，一拍脑门：后面不用想，递归就完事了……其实这个问题也是斐波那契数列问题，因为我们根据上面的分析发现，跳n个台阶的跳法其实就是跳n-1个台阶和n-2个台阶的跳法和，也就是F(N)=F(N-1)+F(N-2);然后结合我们上一个问题的解法，循环反而是最好的实现方法。

题目2：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

Python解法：

# -*- coding:utf-8 -*-
class Solution:
    def jumpFloor(self, number):
        # write code here
        if number==1:
            return 1
        elif number==2:
            return 2
        t1=1
        t2=2
        for i in range(2,number):
            temp=t2
            t2=t1+t2 
            t1=temp
        return t2

然后有一道非常类似的问题：矩形覆盖，其实利用上面的分析方式非常容易分析，（我现在看到2就不由自主的想到两种情况，然后看这两种情况是否和之前的项有关，如果有，很可能是斐波那契数列。斐波那契数列的核心在于规律F(N)=F(N-1)+F(N-2)，当前项与前两项有关联的关系，都可以用斐波那契数列来解决。）

题目3：

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

比如n=3时，2*3的矩形块有3种覆盖方法：

python解法：

# -*- coding:utf-8 -*-
class Solution:
    def rectCover(self, number):
        # write code here
        if number==0:
            return 0
        elif number==1:
            return 1
        t1=1
        t2=1
        for i in range(2,number+1):
            temp=t2
            t2=t1+t2 
            t1=temp
        return t2

根据这种思想，可以解决变态跳台阶问题，说实话我在拿到变态跳台阶问题时第一反应是递归，嵌套在for循环里面递归一求和的函数，后来想起来之前做斐波那契数列的经验，用双重循环解决。可以把第n个台阶的跳法求法归纳为一个函数，F(N)=F(N-1)+F(N-2)+ ……+F(1),我的解法思路就是用一个列表temp保持前N-1项的值，然后再求和得到第N项的跳法，外层循环运行N次得到N想的值，而内层循环则是计算前N项求和过程中的其他项，这么说可能不太清楚，愿意尝试的朋友可以把内层循环封装成一个函数，然后用一个循环套这个函数实现，这样就容易理解了。比如 F(N)求第N项的跳法，但是不能直接F（N）得到结果，需要用一个循环由F(1)一直求过来，简单描述就是这样就是这样

temp={1,2}

for i in range(1:n+1):

temp[i]=F(i)

return temp[i]

题目4：一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

python解法：

# -*- coding:utf-8 -*-
class Solution:
    def __init__(self):
        self.temp=[0,1,2]
    def jumpFloorII(self, number):
        # write code here
        for i in range(3,number+1):
            sum=0
            for j in range(0,i):
                sum=sum+self.temp[j]
            self.temp.append(sum+1)
        return self.temp[number]