算法讲解
后缀数组((SA,Suffix Array)),是将字符串的所有后缀排序得到的数组
一些定义
s(i,j):字符串(S)的第(i)为到第(j)位
suf(i):以 (i) 开头的后缀,即(s(i,n))
sa[i]:将所有后缀排完序后,排名为 (i) 的是原串的第几位(开头位置)
rk[i]:(rank_i)表示(suf(i))的最终排名
经典图片
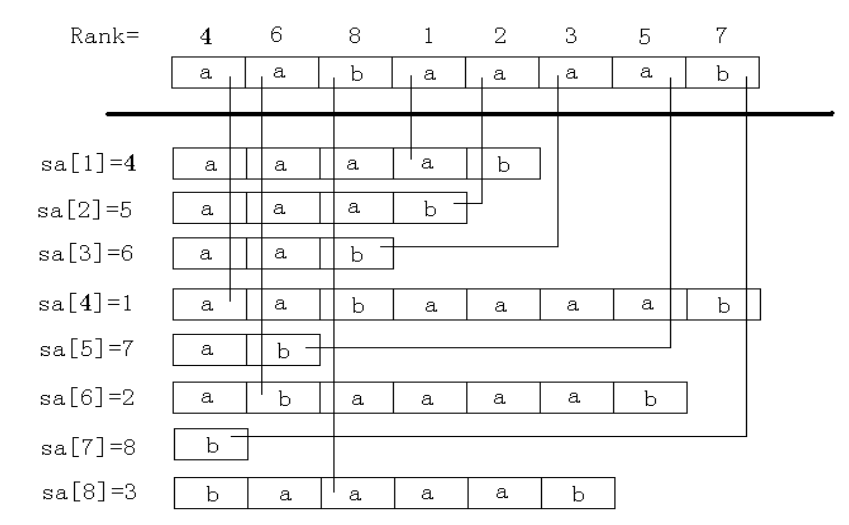
他们满足如下的重要性质:
请务必理解并牢记这两个定义,否则下面会非常绕
思想:倍增
我们依次处理所有 (suf(i)) 的前 (2^0,2^1,2^2,cdots)位的排名,如果两个后缀的前(2^i)位相同,比较这两个后缀第 (2^i+1sim 2^{i+1})的大小。即比较(s(x+2^i+1,x+2^{i+1}))与(s(y+2^i+1,y+2^{i+1}))
而这个结果我们已经在前一轮计算前(2^i)位的时候计算过了
这样我们就可以倍增求解,看看这张图可能会好理解一点
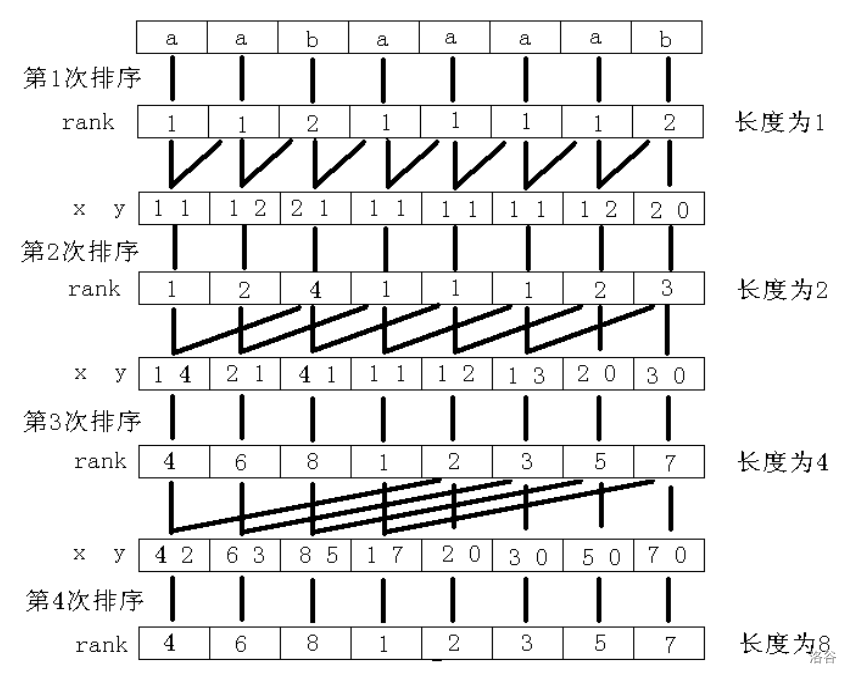
但是排序如果使用(sort),那复杂度会多个(log)
我们发现这个数字由两位拼成,这两位都(< n),考虑使用(O(n))的基数排序
其实思想很好懂,关键是理解下面的代码
理解代码
先放代码
int sa[N],rk[N],sec[N],tot[N],sz,rk1[N];
inline void init(){
for(int i=1;i<=n;++i)rk[i]=s[i],++tot[rk[i]];
for(int i=1;i<=S;++i)tot[i]+=tot[i-1];
for(int i=n;i;--i)sa[tot[rk[i]]--]=i;
}
inline void bucsort(){
memset(tot,0,(sz+1)<<2);
for(int i=1;i<=n;++i)++tot[rk[i]];
for(int i=1;i<=sz;++i)tot[i]+=tot[i-1];
for(int i=n;i;--i)sa[tot[rk[sec[i]]]--]=sec[i],sec[i]=0;
}
inline void getsa(){
init();
for(int k=1;k<=n;k<<=1){
int cnt=0;
for(int i=n-k+1;i<=n;++i)sec[++cnt]=i;
for(int i=1;i<=n;++i)if(sa[i]>k)sec[++cnt]=sa[i]-k;
bucsort();
memcpy(rk1+1,rk+1,n<<2);
sz=1;rk[sa[1]]=1;
for(int i=2;i<=n;++i)
rk[sa[i]]=(rk1[sa[i]]==rk1[sa[i-]]&&rk1[sa[i]+k]==rk1[sa[i-1]+k])?sz:++sz;
if(sz==n)return;
}
}
数组的含义
sa,rk:意义没有太大变化,只是把全局排名改成前(2^i)位的排名。对于前(2^i)位相同的,sa可以为任意符合条件的不同整数,而rk都相同
sec[i]:第二关键字排名为 (i) 的数在原串中的位置
rk1:rk拷贝出来的数组,拷贝一遍的意义下面会说
tot[i]:第一关键字为(i)的出现次数/前缀和
初始化
inline void init(){
for(int i=1;i<=n;++i)rk[i]=s[i],++tot[rk[i]];
for(int i=1;i<=S;++i)tot[i]+=tot[i-1];
for(int i=n;i;--i)sa[tot[rk[i]]--]=i;
}
即(2^0)的情况,(rk)就是这一位的值,对(tot)做一次前缀和
sa[tot[rk[i]]--]=i的意义是:对于第(i)位,它的排名为第一关键字小于等于自己的个数,sa[tot[rk[i]]]=i。自己用完了之后,与(i)的(rk)相同的数中,等于自己的数的个数会减少,所以tot[rk[i]]--]
找出 sec
首先对于第(n-2^i+1sim n)位,第二关键字都是(0),肯定是最小的,放在最前面
对于(sa[i]>2^x)的位置,它会作为(sa[i]-2^x)位置的第二关键字。因为(sa[i])是排名为(i)的后缀开头,保证了第二关键字的递增
基数排序
与上面极其类似
在(rk)相同的情况下倒叙枚举(sec),这样保证第二关键字在第一关键字相同的情况下满足条件
求出新的rk
首先确定(rk[sa[1]]=1)
因为(rk)会变,把它复制一遍
如果自己与前一个第一、第二关键字排名都相同,那么这两个依然是相同的,(rk[sa[i]]=rk[sa[i-1]]),否则,(rk[sa[i]]=rk[sa[i-1]]+1)
记录有几个不同的值,如果有(=n)个就已经排序完成了,不必要继续了
后缀数组的重要性质
又一些定义
height[i]:suf(sa[i])与suf(sa[i-1])的最大公共前缀(LCP)。即排完序后相邻两个的LCP。特别的,(height[1]=0)
h[i]:(h[i]=height[rank[i]])。即(suf(i))与排名在(i)之前的最近的一个的LCP
重要性质
- (LCP(i,j)=minlimits_{k=rk[i]+1}^{rk[j]}height[k](rk[i]<rk[j]))
也就是说,求出(height)之后,可以(O(1))ST表求出两个串的LCP。求LCS(最大公共后缀)的话就把原字符串reverse一遍即可
- (h[i]ge h[i-1]-1)
首先(h[i-1]le 1)的时候显然成立
否则把第一个字符删去,剩下的一定匹配。结合下面这个图更好理解

于是我们可以在求出(sa)和(rk)之后(O(n))求出height
int height[N];
inline void getheight(){
int k=0;
for(int i=1;i<=n;++i){
if(rk[i]==1)continue;
if(k)--k;
int pos=sa[rk[i]-1];
while(pos+k<=n&&i+k<=n&&s[pos+k]==s[i+k])++k;
height[rk[i]]=k;
}
}
这篇文章就大概讲这些了,具体的使用可以参见后缀数据结构的使用