棋盘分割
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 501 Accepted Submission(s): 248
Problem Description
将一个8*8的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了(n-1)次后,连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行) 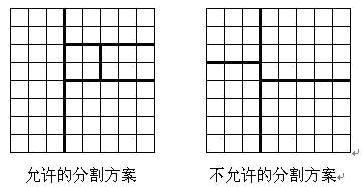
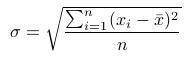 ,其中平均值
,其中平均值 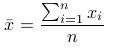 xi为第i块矩形棋盘的总分。 请编程对给出的棋盘及n,求出O'的最小值。
xi为第i块矩形棋盘的总分。 请编程对给出的棋盘及n,求出O'的最小值。

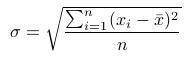 ,其中平均值
,其中平均值 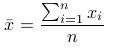 xi为第i块矩形棋盘的总分。 请编程对给出的棋盘及n,求出O'的最小值。
xi为第i块矩形棋盘的总分。 请编程对给出的棋盘及n,求出O'的最小值。 Input
第1行为一个整数n(1 < n < 15)。 第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
Output
仅一个数,为O'(四舍五入精确到小数点后三位)。
Sample Input
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3
Sample Output
1.633
题解:
re了半天,知道真相的我眼泪流了下来,TMD,步数是15,我开的是10;
记忆化搜索,dp[x1][y1][x2][y2]代表到这个矩形状态的最小s[i]平方和;
下面是大神的详细解释:
n刀切割棋盘
下面是8*8的棋盘,每个数字代表棋盘对应点的权值,问切割n刀后,每一块的和 的均方差最小是多少
均方差的公式需要先化简:
由上式得,均方差最小 显然是要 Xi^2 最小
d[k][x1][y1][x2][y2]代表棋盘从(x1,y1)->(x2,y2)已经切了k刀 获得的最小的平方和
用sum[i][j] 代表 从(1,1)点 到 (i,j)点的权值和
这样答案就是 dp[n][1][1][8][8]/n -(sum[8][8]/n)^2
用S[ (x1,y1) ,( x2,y2) ] 代表 这两点间的权值和
这里用递归dp
状态转移方程:
d[k][x1][y1][x2][y2]=
Min{ 横向切: d[k-1] +剩下未切部分的平方和,纵向切:d[k-1]+剩下未切部分的平方和 }
横向切的最优解就是 Min{ d[ k-1,(x1,y1) , ( i ,y2) ] + S[ (i +1,y1) , ( x2 ,y2) ] , d[ k-1,(i+1,y1) , ( x2 ,y2) ] + S[ (x1,y1) , ( i ,y2) ] } ( x1<= i <x2)
代码:
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> #include<vector> using namespace std; const int INF=0x3fffffff; #define mem(x,y) memset(x,y,sizeof(x)) #define SI(x) scanf("%d",&x) #define PI(x) printf("%d",x) #define SD(x) scanf("%lf",&x) #define P_ printf(" ") typedef long long LL; const int MAXN=10; double dp[20][MAXN][MAXN][MAXN][MAXN];//卧槽 int s[MAXN][MAXN]; double ss[MAXN][MAXN][MAXN][MAXN]; double SUM(int x1,int y1,int x2,int y2){ if(ss[x1][y1][x2][y2]>=0)return ss[x1][y1][x2][y2]; int temp=s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]; return ss[x1][y1][x2][y2]=temp*temp; } double dfs(int k,int x1,int y1,int x2,int y2){ if(k==1){ dp[k][x1][y1][x2][y2]=SUM(x1,y1,x2,y2); return dp[k][x1][y1][x2][y2]; } if(dp[k][x1][y1][x2][y2]>=0)return dp[k][x1][y1][x2][y2]; double temp = 99999999999; for(int i=x1;i<x2;i++){ temp=min(temp,SUM(x1,y1,i,y2)+dfs(k-1,i+1,y1,x2,y2)); temp=min(temp,SUM(i+1,y1,x2,y2)+dfs(k-1,x1,y1,i,y2)); } for(int i=y1;i<y2;i++){ temp=min(temp,SUM(x1,i+1,x2,y2)+dfs(k-1,x1,y1,x2,i)); temp=min(temp,SUM(x1,y1,x2,i)+dfs(k-1,x1,i+1,x2,y2)); } return dp[k][x1][y1][x2][y2]=temp; } int main(){ int N; while(~SI(N)){ int temp; mem(ss,-1);mem(s,0);mem(dp,-1); for(int i=1;i<=8;i++){ for(int j=1;j<=8;j++){ scanf("%d",&temp); s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+temp; } } double ave=s[8][8]*1.0/N; double ans=dfs(N,1,1,8,8); //printf("%lf %d %lf ",ans,s[8][8],ave); printf("%.3lf ",sqrt(ans*1.0/N-ave*ave)); } return 0; }
