斐波那契数列 矩阵求法 优化

矩阵乘法+空间换时间(减少乘法，取模运算)

 　　数列的递推公式为：f(1)=1，f(2)=2，f(n)=f(n-1)+f(n-2)(n>=3)

　　 用矩阵表示为：

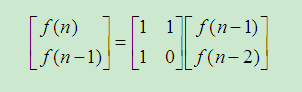
　　进一步，可以得出直接推导公式：

static int Fibonacci(int n)
     {
       if (n <= 1)
         return n;
 
       int[,] f = { { 1, 1 }, { 1, 0 } };
       Power(f, n - 1);
 
       return f[0, 0];
     }
 
     static void Power(int[,] f, int n)
     {
       if (n <= 1)
         return;
 
       int[,] m = { { 1, 1 }, { 1, 0 } };
 
       Power(f, n / 2);
       Multiply(f, f);
 
       if (n % 2 != 0)
         Multiply(f, m);
     }
 
     static void Multiply(int[,] f, int[,] m)
     {
       int x = f[0, 0] * m[0, 0] + f[0, 1] * m[1, 0];
       int y = f[0, 0] * m[0, 1] + f[0, 1] * m[1, 1];
       int z = f[1, 0] * m[0, 0] + f[1, 1] * m[1, 0];
       int w = f[1, 0] * m[0, 1] + f[1, 1] * m[1, 1];
 
       f[0, 0] = x;
       f[0, 1] = y;
       f[1, 0] = z;
      f[1, 1] = w;
     }

 　　由于矩阵乘法满足结合律，在程序中可以事先给定矩阵的64，32，16，8，4，2，1次方，加快程序的执行时间。（有些题目需要取模运算，也可以事先进行一下）。给定的矩阵次幂，与二进制有关是因为，如下的公式存在解，满足Xi={0或1}： 

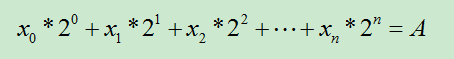
为了保证解满足 Xi={0或1}，对上述公式的求解从右向左，即求解顺序为Xn，Xn-1,Xn-2,....,X1,X0。

　　完整代码实现如下：

///求解fac(n)%100000，其中n为大于等于3的正整数
#include<stdio.h>
#include<math.h>
long long fac_tmp[6][4]={   ///存放矩阵次幂
                    ///位置：00 01 10 11
                   {24578,78309,78309,46269},   ///32次幂%100000
                   {1597,987,987,610},  ///16次幂%100000
                   {34,21,21,13},   ///8次幂%100000
                   {5,3,3,2},   ///4次幂%100000
                   {2,1,1,1},   ///2次幂%100000
                   {1,1,1,0},   ///1次幂%100000
                   };
void fac(int);

int main()
{
    int n;
    scanf("%d",&n);
    fac(n);
    return 1;
}

void fac(int k) ///k>=3
{
    int i;
    long long t00=1,t01=1,t10=1,t11=0;  ///表示矩阵的1次幂
    long long a,b,c,d;
    k=k-3;  ///公式中是n-2次幂，(t00,t01,t10,t11)表示1次幂。所以一共减3次
    for(i=k;i>=32;i=i-32)   ///对于大于等于32的k;
    {
        a=(t00*fac_tmp[0][0]+t01*fac_tmp[0][2])%100000;
        b=(t00*fac_tmp[0][1]+t01*fac_tmp[0][3])%100000;
        c=(t10*fac_tmp[0][0]+t11*fac_tmp[0][2])%100000;
        d=(t10*fac_tmp[0][1]+t11*fac_tmp[0][3])%100000;
        t00=a;  t01=b;  t10=c;t11=d;
    }

    i=4;
    while(i>=0)    ///对于小于32的k(16,8,4,2,1);
    {
        if(k>=(long long)pow(2,i))  ///如果k大于某一个2的次幂
        {

            a=(t00*fac_tmp[5-i][0]+t01*fac_tmp[5-i][2])%100000; ///(5-i)：矩阵的2的i次幂在数组fac_tmp中的位置为fac_tmp[5-i]
            b=(t00*fac_tmp[5-i][1]+t01*fac_tmp[5-i][3])%100000;
            c=(t10*fac_tmp[5-i][0]+t11*fac_tmp[5-i][2])%100000;
            d=(t10*fac_tmp[5-i][1]+t11*fac_tmp[5-i][3])%100000;
            t00=a;  t01=b;  t10=c;t11=d;
            k=k-(int)pow(2,i);
        }
        i--;
    }

    a=(t00*2+t01*1)%100000;
    printf("%lld
",a);
}