wdnmd,真就全都不会做呗。
T1 字符串值
题意描述
定义 (S[l:r]) 表示字符串 (S) 中第 (l) 个到第 (r) 个字符构成的子串,(|S|) 表示字符串 (S) 的长度。
对于字符串 (S),我们定义 (fail_i) 等于最大的 (x),满足 (x<i) 且 (s[1:x] = s[i-x+1:i]) 。将每个 (0leq ileq |S|) 看成结点,除 (i=0) 以外,(i) 向 (fail_i) 连边,会形成一颗树,根是 (0)(根深度默认为 (-1)),我们将其称为 (fail) 树。
定义 (F(S)) 为 (S) 的 (fail) 树上的除了 (0) 号节点外所有节点的深度和。定义 (displaystyle G(S) = sum_{1leq lleq rleq |S|} F(S[l:r])),即对于 (S) 所有子串的 (F) 求和。
一开始有一个空串 (S),接下来有 (n) 次操作,每次在空串末尾添加一个小写字母,要求你能够快速求出 。由于答案很大,请对 (1e9+7) 取模。
数据范围:(nleq 2 imes 10^5)
solution
后缀自动机套树链剖分。
对于一个字符串 (s), 他的 (fail) 树上的一个节点 (i), 对应的是 (s) 的一个前缀,即 (s[1....i]) 。(i) 的深度则表示有多少个 (j) 满足 (s[1...j] = s[i-j+1...i]) 。那么 (F(s)) 则表示 (s) 的前缀的所有符合条件的 (j) 的数量。
根据这个我们考虑 (G(s)) 怎么算,假设 (s) 的两个子串 (s_1,s_2) 相等,对应的区间分别为:([l_1,r_1],[l_2,r_2])即:

不难发现 (s[l_1,r_2]) 有一个符合条件的 (j) 使得:(s_1 = s_2) 。同时 (s[l_1,r_2]) 可以作为 (s[l_1,r]) ((r_2leq rleq len(s)))前缀。所以 (s[l_1,r_2]) 对 (G(s)) 的贡献则为:(len(s)-r_2+1) 。
对于这道题,我们考虑离线处理。先求出以 (i) 为右端点的 (s_2) 满足条件的 ((s_1,s_2)) 的数量,设其为 (h(i)), 求一遍前缀和就可以得到以 (i) 为右端点的字符串的 (F(s)) 的和,在求一遍前缀和就可以得到 (G(s[1..i])) 。
先用后缀自动机建出 (partent) 树来。然后考虑每加入一个字符串产生的贡献。
设当前字符串 (s) 在后缀自动机上对应的节点为 (x) ,那么 (x) 到根节点的路径上的点就可以表示 (s) 的所有后缀。
显然这些后缀都可以作为 (s_2) ,对应的 (s_1) 的个数即为 (s_2) 在 (s[1...i-1]) 出现的次数。
设 (cnt(u)) 表示没加入第 (i) 个字符之前的 (u) 的 (endpos) 的大小。
则有:(h(i) = displaystylesum_{uin{x的祖先}} cnt(u) imes (maxlen(u)-maxlen(fa(u))))
(maxlen(u)) 在建后缀自动机的时候就可以统计出来。
(cnt(u)) 表示的是 (u) 的子树中 (np) 节点的个数,每次把 (x) 到根节点的路径上的点的 (cnt(u)+1) 即可。
用线段树和树链剖分就可以快速维护出 (cut(u)) 。
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int p = 1e9+7;
const int N = 4e5+10;
int n,m,tot,cnt,last,num;
int head[N],len[N],link[N],tr[N][26],st[N];
int dep[N],fa[N],top[N],siz[N],son[N],ans[N],dfn[N],id[N];
char s[N];
struct node
{
int to,net;
}e[N<<1];
struct Tree
{
int lc,rc;
int sum,w,tag;
}Tr[N<<2];
#define l(o) Tr[o].lc
#define r(o) Tr[o].rc
#define sum(o) Tr[o].sum
#define w(o) Tr[o].w
#define tag(o) Tr[o].tag
void add(int x,int y)
{
e[++tot].to = y;
e[tot].net = head[x];
head[x] = tot;
}
void Extend(int ch)
{
int cur = ++cnt, p = last;
len[cur] = len[last] + 1;
for(; p && !tr[p][ch]; p = link[p]) tr[p][ch] = cur;
if(!p) link[cur] = 1;
else
{
int x = tr[p][ch];
if(len[x] == len[p] + 1) link[cur] = x;
else
{
int y = ++cnt;
len[y] = len[p] + 1;
memcpy(tr[y],tr[x],sizeof(tr[x]));
link[y] = link[x];
link[x] = link[cur] = y;
while(p && tr[p][ch] == x)
{
tr[p][ch] = y;
p = link[p];
}
}
}
last = cur;
}
void get_tree(int x)
{
dep[x] = dep[fa[x]] + 1; siz[x] = 1;
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa[x]) continue;
fa[to] = x;
get_tree(to);
siz[x] += siz[to];
if(siz[to] > siz[son[x]]) son[x] = to;
}
}
void dfs(int x,int topp)
{
top[x] = topp; dfn[x] = ++num; id[dfn[x]] = x;
if(son[x]) dfs(son[x],topp);
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa[x] || to == son[x]) continue;
dfs(to,to);
}
}
void up(int o)
{
w(o) = (w(o<<1) + w(o<<1|1)) % p;
sum(o) = (sum(o<<1) + sum(o<<1|1)) % p;
}
void cover(int o,int val)
{
tag(o) += val;
sum(o) = (sum(o) + w(o) * val % p) % p;
}
void down(int o)
{
if(tag(o))
{
cover(o<<1,tag(o));
cover(o<<1|1,tag(o));
tag(o) = 0;
}
}
void build(int o,int L,int R)
{
l(o) = L, r(o) = R;
if(L == R)
{
int x = id[L];
w(o) = len[x]-len[link[x]];
return;
}
int mid = (L+R)>>1;
build(o<<1,L,mid);
build(o<<1|1,mid+1,R);
up(o);
}
void chenge(int o,int L,int R)
{
if(L <= l(o) && R >= r(o))
{
cover(o,1);
return;
}
down(o);
int mid = (l(o)+r(o))>>1;
if(L <= mid) chenge(o<<1,L,R);
if(R > mid) chenge(o<<1|1,L,R);
up(o);
}
int query(int o,int L,int R)
{
int res = 0;
if(L <= l(o) && R >= r(o)) return sum(o);
down(o);
int mid = (l(o) + r(o))>>1;
if(L <= mid) res = (res + query(o<<1,L,R)) % p;
if(R > mid) res = (res + query(o<<1|1,L,R)) % p;
return res;
}
void modify(int x,int y)
{
while(top[x] != top[y])
{
if(dep[top[x]] < dep[top[y]]) swap(x,y);
chenge(1,dfn[top[x]],dfn[x]);
x = fa[top[x]];
}
if(dep[x] >= dep[y]) swap(x,y);
chenge(1,dfn[x],dfn[y]);
}
int get_ans(int x,int y)
{
int res = 0;
while(top[x] != top[y])
{
if(dep[top[x]] < dep[top[y]]) swap(x,y);
res = (res + query(1,dfn[top[x]],dfn[x])) % p;
x = fa[top[x]];
}
if(dep[x] >= dep[y]) swap(x,y);
res = (res + query(1,dfn[x],dfn[y]));
return res;
}
int main()
{
freopen("string.in","r",stdin);
freopen("string.out","w",stdout);
scanf("%d%s",&n,s+1);
last = cnt = 1;
for(int i = 1; i <= n; i++) Extend(s[i]-'a'), st[i] = last;
for(int i = 2; i <= cnt; i++) add(link[i],i), add(i,link[i]);
get_tree(1); dfs(1,1); build(1,1,cnt);
for(int i = 1; i <= n; i++)
{
ans[i] = get_ans(1,st[i]);
modify(1,st[i]);
}
for(int i = 1; i <= n; i++) ans[i] = (ans[i] + ans[i-1]) % p;
for(int i = 1; i <= n; i++)
{
ans[i] = (ans[i] + ans[i-1]) % p;
printf("%d
",ans[i]);
}
fclose(stdin); fclose(stdout);
return 0;
}
T2 花钟计数
题意描述
花卉时钟一直矗立在镜湖边。尽管不能留住时间,但它提醒人们时间的过去,使人们想起过去美好的时光。
在花卉时钟的边缘一共有 (2n) 朵花,顺时针依次编号为 (1) 到 (2n),每一朵花的颜色为 (n) 种可能的颜色中的一种。对于每种颜色,恰有两朵花是这种颜色的,这两朵花的距离要么不大于 (2),要么等于 (n)。另外,如果花 (u) 和花 (v) 有相同的颜色,那么 (u) 对面的那一朵花和 (v) 对面的那一朵花的颜色也应该相同——对称是美的!
形式化的说,两朵花之间的距离是 (1) 加上夹在以这两朵花为端点的劣弧(或者半圆)之间的花的数目。下面是当 (n=6) 时一种可能的安排颜色的方式:
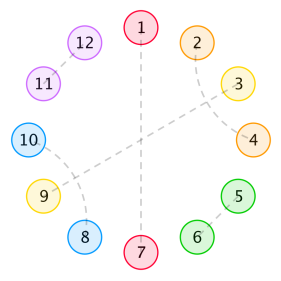
我们定义一种安排方式的美感为被所有相对(距离为 (n))且颜色相同的花分开的连续段的长度的乘积。换句话说,为了计算美感,我们先在环上移除那些与相对的花颜色相同的花。然后,它的美感就是剩下的连续段长度的乘积。注意到本题中包括了长度为 (0) 的那些连续段。在某种安排方式中,如果没有任何一朵花使得与它相对的花的颜色与它相同,那么这种安排方式的美感为 00。比如说,上图的安排方式的美感等于 (1 imes 3 imes 1 imes 3=9)——这些连续段为 ({2},{4,5,6},{8},{10,11,12})。
尽管保持了这些约束条件,但是可能的安排方式会有多种,你需要计算出所有可能的安排方式的美感之和,对 (998244353) 取模。两个安排方式被视为不同的,当且仅当存在一个二元组 ((u,v)(1leq u,vleq 2n)) 使得在其中一种安排方式中花 (u) 和花 (v) 颜色相同而在另一种安排方式中颜色不同。
数据范围:(nleq 50000)
solution
计数套分治 (NTT)
自己的计数水平大概是小学生水平,看了半天题解都没看懂 /cy。
T3 平面标记
题意描述
平面上有 (n) 个点,第 (i) 个点的坐标为 ((x_i,y_i))。
你会依次收到 (m) 个操作,第 (i) 个操作形如 (k_i,a_i),表示你需要标记所有满足 (y_j>{k_iover x_j^{a_i}}) 的点 (j)。
在执行完所有操作后,你想知道每个点在哪次操作中第一次被标记。
数据范围:(1leq nleq m,0<x,y<1000,0<k<10^6,0<a<10)。
solution
线段树分治+半平面交或者整体二分套半平面交。
考虑先转化一下条件,即:
(y_j>{k_iover x_j^{a_i}} Leftrightarrow y_j imes x_j^{a_i} > k_i) 。
对于两个大数比较大小,我们有一个很常用的技巧就是分别对其去 (ln),则有:
(ln y_j + a_i ln x_j > ln k_i)
这显然是一个半平面交的形式。将询问的点 ((x,y)) 变为 ((ln x,ln y)) ,并把所有的限制条件取反,二分一个答案 (t),
然后问题就转化为判断前 (t) 条直线所组成的半平面是否包含 ((ln x,ln y)) 这个点。
注意到给定的半平面一定是一条斜率小于 0 的直线下方的区域,因此组成的半平面交一定是一个上凸壳下方的区域,可以直接在凸壳上二分得到横坐标范围包含询问点的线段来判断。
具体地,我们对所有半平面维护一棵线段树,在线段树上的每个结点记录该结点对应区间的上凸壳,询问一个点时就直接在线段树上二分。
时间复杂度:(O(nlogn^2)) 。
代码
//太难写了,咕咕咕