树上最远点对是啥啊?嗯,树的直径吗?恭喜你,答对了!
这篇博客可能内容较水....
我们都知道树上距离最远的的两个点的距离就是树的直径,而且这两个点就是直径的两个端点.
一般求树直径的方法就两个:树形dp和两遍bfs。
话说为啥两遍bfs求出来的就是直径的两个端点???
这里简单的证明一下:
首先我们需要证明一个引理:对于树上任意一个点,与他距离最远的点一定是直径的一个端点。
而证明这个引理需要两步:
首先这个点在树的直径上:
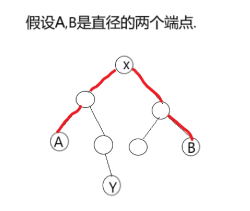
如图,如果存在一个点Y使得X到Y的距离大于到A和到B的距离的话,显然B-X-Y也就是B到Y的距离要大于B到A的距离,这使,AB就不是直径的两个端点了,故不成立!也就是说如果存在其他的点距离比到两个端点的距离更大,我们完全可以构造一个原来直径更长的距离出来...
当这个点不在树的直径上时:

如图,(这个图怎么这么丑......)当X距离Y大于到A和到B的距离时,我们可以显然的发现此时,B到Y的距离是大于B到A的距离的,我们观察X到Y与直径的交点Z,我们可以这样的理解,此时Z是偏向A的,而X->Y大于X->A,两者都减去X->Z,则必有Z->Y大于Z->A,此时对B来说更长的链就走向Y了,故假设不成立.
证毕!
有了这个结论,我们就容易知道了第一次bfs找到最远的一个点,这个点一定是直径的一个端点,再做一次bfs就找到了直径的另一个端点了。
其实除了这两种做法外,还有其他的做法,我们可以预处理RMQ处理lca,先随机选两个点作为直径,然后枚举每一个点,比较三个点形成的三个距离,距离最大的两个点保留,最后留到最后的一定是直径的两个端点了。这个应该很好证明吧!我们考虑当枚举到一个端点时,他必然会留下来,这个应该可以类似上面的方法证明一下,这里就略过了...所以这样扫过去另一个端点一定也会留下来,所以这算是一个简单的方法吧,起码实现起来比较简单。
这里安利一道比较秒的题目:
漂亮的公园
看到题目的第一眼,啥?求任意两个颜色的最远距离,肯定需要啥比较高级的数据结构,啥树剖啊,啥平衡树啊,应该是有可能的吧,后来再想想了,完了,我不会了....
后来看到题解,原来这样的......
首先我们思考两个颜色的最远距离一定是两个颜色直径的两个端点的四个距离中的较大值。
要证明上面的结论,我们一步一步来,先来证明一个弱化版的问题,一个点到一个颜色的最远距离一定是到颜色的直径的一个端点的距离。
咦,这不是和上面说过的一样吗?就略过了...之后就只用考虑一个颜色直径的两个端点对另一个颜色进行距离的比较,发现这还是弱化版的问题,于是就变成了两个颜色的共四个点的距离比较,由于这里的颜色比较多,所以直接用上面比较暴力的方法扫一下比较便捷,且预处理RMQ的话,复杂度还是O(n)的,那这道题就到这吧!
//不等,不问,不犹豫,不回头.
#include<bits/stdc++.h>
#define _ 0
#define ls p<<1
#define db double
#define rs p<<1|1
#define RE register
#define P 999911659
#define ll long long
#define INF 1000000000
#define get(x) x=read()
#define PLI pair<ll,int>
#define PII pair<int,int>
#define pb(x) push_back(x)
#define ull unsigned long long
#define put(x) printf("%d
",x)
#define putl(x) printf("%lld
",x)
#define rep(x,y,z) for(RE int x=y;x<=z;++x)
#define fep(x,y,z) for(RE int x=y;x>=z;--x)
#define go(x) for(RE int i=link[x],y=a[i].y;i;y=a[i=a[i].next].y)
using namespace std;
const int N=1e5+10;
int link[N],tot,n,c[N],b[N],num,q,d[N],f[N<<1][25],id,dfn[N],Log[N<<1];
struct edge{int y,next;}a[N<<1];
vector<int>col[N];
map<int,int>mp;
char *fs,*ft,buf[1<<15];
inline char getc() {return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;}
inline int read()
{
int x=0,ff=1;
char ch=getc();
while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getc();}
while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getc();}
return x*ff;
}
inline int find(int x) {return lower_bound(b+1,b+num+1,x)-b;}
inline void add(int x,int y)
{
a[++tot].y=y;a[tot].next=link[x];link[x]=tot;
a[++tot].y=x;a[tot].next=link[y];link[y]=tot;
}
inline void dfs(int x,int fa)
{
d[x]=d[fa]+1;
dfn[x]=++id;f[id][0]=x;
go(x) if(y!=fa)
{
dfs(y,x);
f[++id][0]=x;
}
}
inline int cmp(int a,int b) {return d[a]<d[b]?a:b;}
inline int lca(int a,int b)
{
int x=dfn[a],y=dfn[b];
if(x>y) swap(x,y);
int t=Log[y-x+1];
return cmp(f[x][t],f[y-(1<<t)+1][t]);
}
inline int dis(int a,int b) {return d[a]+d[b]-2*d[lca(a,b)];}
int main()
{
//freopen("1.in","r",stdin);
get(n);get(q);
rep(i,1,n) get(c[i]),b[i]=c[i];
rep(i,1,n-1) add(read(),read());
sort(b+1,b+n+1);
num=unique(b+1,b+n+1)-b-1;
rep(i,1,n)
{
int d=find(c[i]);col[d].pb(i);
mp[c[i]]=d;
}
dfs(1,0);
rep(i,2,id) Log[i]=Log[i>>1]+1;
rep(j,1,Log[id]) rep(i,1,id-(1<<j)+1) f[i][j]=cmp(f[i][j-1],f[i+(1<<j-1)][j-1]);
rep(i,1,num)
{
rep(j,2,col[i].size()-1)
{
int dis1=dis(col[i][0],col[i][1]);
int dis2=dis(col[i][0],col[i][j]);
int dis3=dis(col[i][1],col[i][j]);
if(dis1>=dis2&&dis1>=dis3) continue;
else if(dis2>=dis1&&dis2>=dis3) col[i][1]=col[i][j];
else if(dis3>=dis1&&dis3>=dis2) col[i][0]=col[i][j];
}
}
rep(i,1,q)
{
int get(x),get(y);
if(mp.find(x)==mp.end()) {puts("0");continue;}
if(mp.find(y)==mp.end()) {puts("0");continue;}
x=mp[x];y=mp[y];
int ans=0;
rep(w1,0,min(1,(int)col[x].size()-1)) rep(w2,0,min(1,(int)col[y].size()-1))
ans=max(ans,dis(col[x][w1],col[y][w2]));
put(ans);
}
return (0^_^0);
}
//以吾之血,铸吾最后的亡魂.